1.5 Алгоритм вычисления интеграла функции, заданной

таблицей с неравноотстоящими узлами, по методу прямоугольников

Для приближенного вычисления используем формулу (2.1). Предполагаются известными точки (х₀; у₀), (х₁;y₁),…, (x_i; y_i),…, (x_n; y_n).

Программа реализует алгоритм, основанный на следующих рекуррентных соотношениях:

S₀=0, S_i=S_i-1+y_i (x_i-x_i-1), (i=1,2,...,n)

Тогда

.

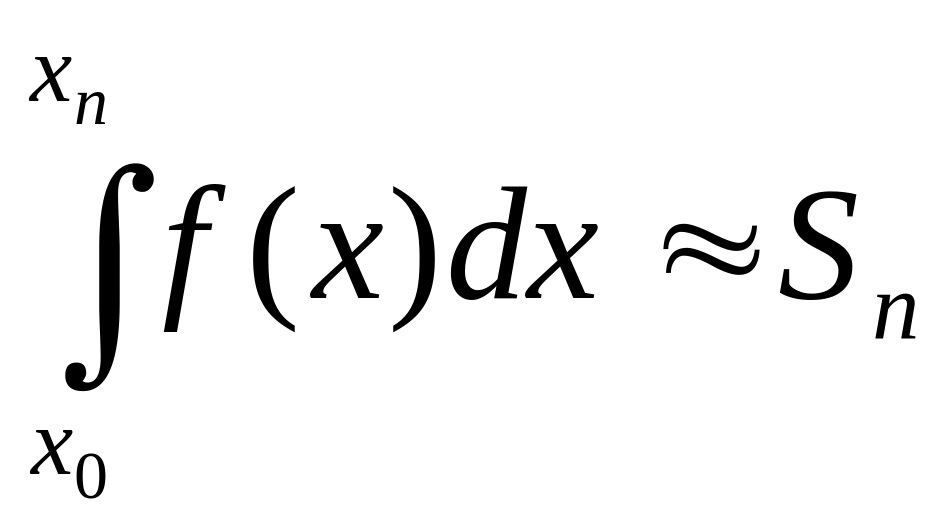2 Формула трапеций

2.1 Вывод формулы

Формула трапеций основана на том, что на отрезке [х₀; х₀ + h] дугу кривой у= f (x) заменяют хордой, стягивающей концы этой дуги (рис. 2.3), т. е. производят линейное интерполирование функции у= f(x). При этом площадь криволинейной трапеции заменяют площадью трапеции с основаниями f(x₀) и f(х₀+h) и высотой h, следовательно,

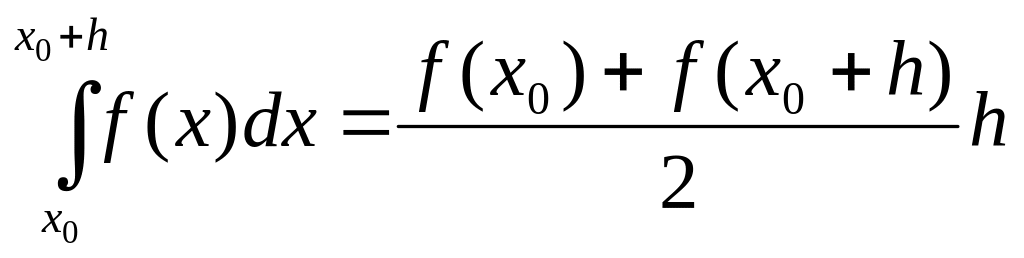
Отсюда, чтобы вычислить , разобьем отрезок [а; b] на n равных частичных отрезков, так что шаг .

Проведем через точки деления ординаты и заменим данную кривую ломаной, отрезки которой соединяют концы двух соседних ординат. Криволинейная трапеция при этом заменится на фигуру, состоящую из n трапеций (рис. 2.4), высоты которых h, а основания – ординаты у_i=f(x_i), ( ), в точках деления. Площадь такой фигуры, как видно из (4), определяется суммой площадей элементарных трапеций.

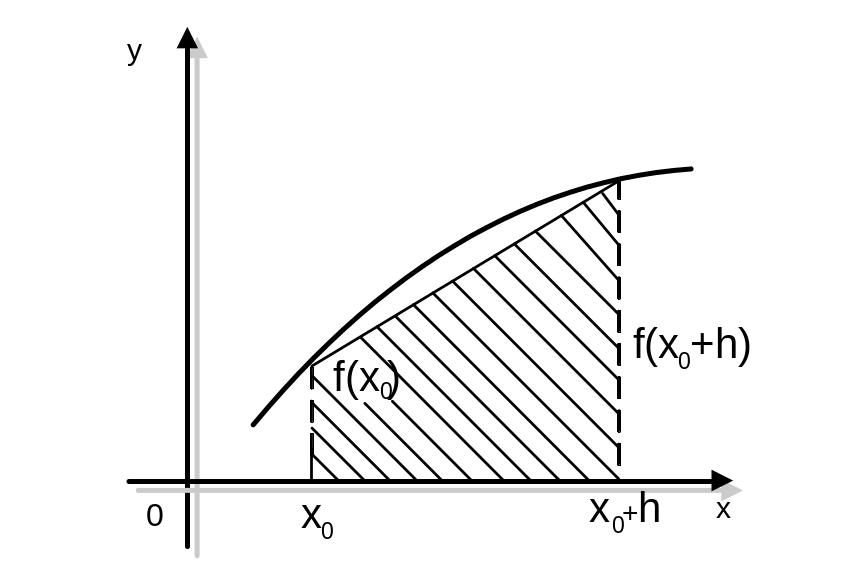Рисунок 2.3 – Линейное интерполирование функции

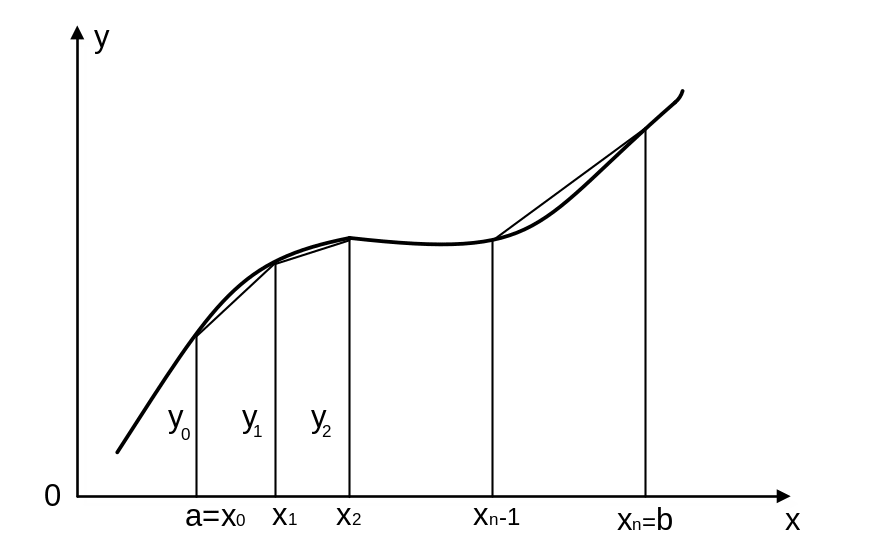
Рисунок 2.4 – Замена криволинейной трапеции фигурой из n трапеций

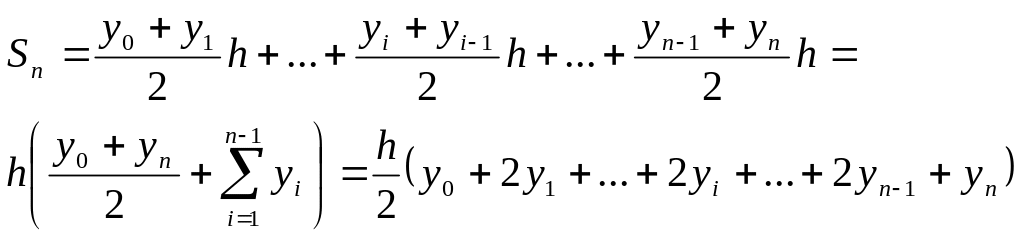(4)

Полученную для вычисления интеграла формулу

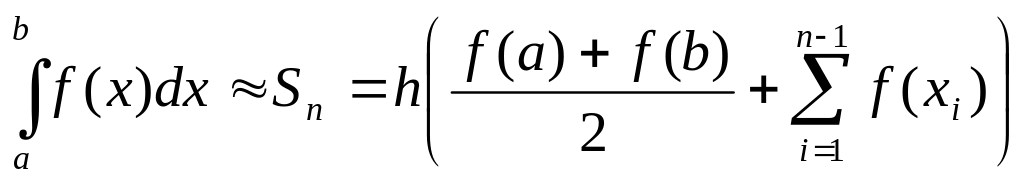(5)

называют формулой трапеций.

2.2 Оценка погрешности формул прямоугольников и трапеций

Понятно, что приближенный результат следует использовать лишь тогда, когда известна его оценка.

Из теории приближенных методов вычислений известна оценка абсолютных погрешностей формул прямоугольников и трапеций :

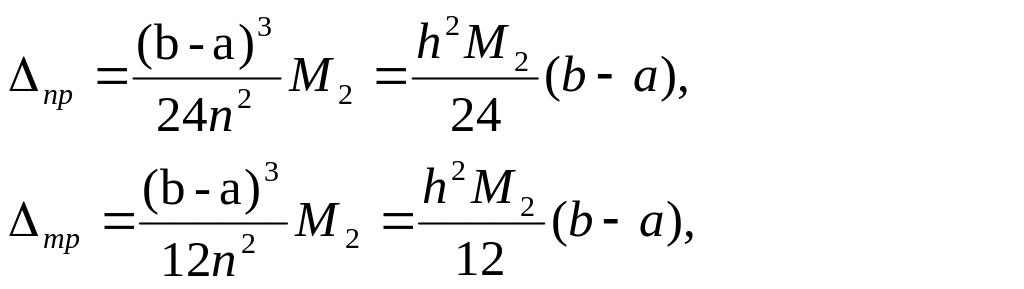(6)

где , f(x) — подынтегральная функция, [a; b] —отрезок интегрирования, h – шаг интегрирования, ( ). Таким образом, если на [a; b] можно найти М₂, то при заданном n (или h) по формулам (6) определяем абсолютную погрешность соответствующих приближенных результатов.

Из сравнения формул (1) - (3) и (5) и формул для их погрешностей (6) можно заключить, что они одинаково трудоемки и дают примерно одинаковой точности результат (погрешность порядка h²). Поэтому ни у одного из этих методов нет преимущества перед другим.

Замечание. Если функция f(х) задана таблично, то в формулах (6) f"(х) можно заменить на конечную разность . Так что

3 Формула Симпсона

Более точной, чем формула трапеций, является формула Симпсона. Для достижения той же точности в ней можно брать меньшее число n участков разбиения и соответственно больший шаг h, а при одном и том же шаге h, (т. е. при том же объеме вычислений), она дает меньшие абсолютную и относительную погрешности.

Формулу Симпсона можно получить следующим образом. Разобьем участок [а, b] на четное число частей n = 2m точками

а=x₀<x₁<...<x_n-1<x_n=b .

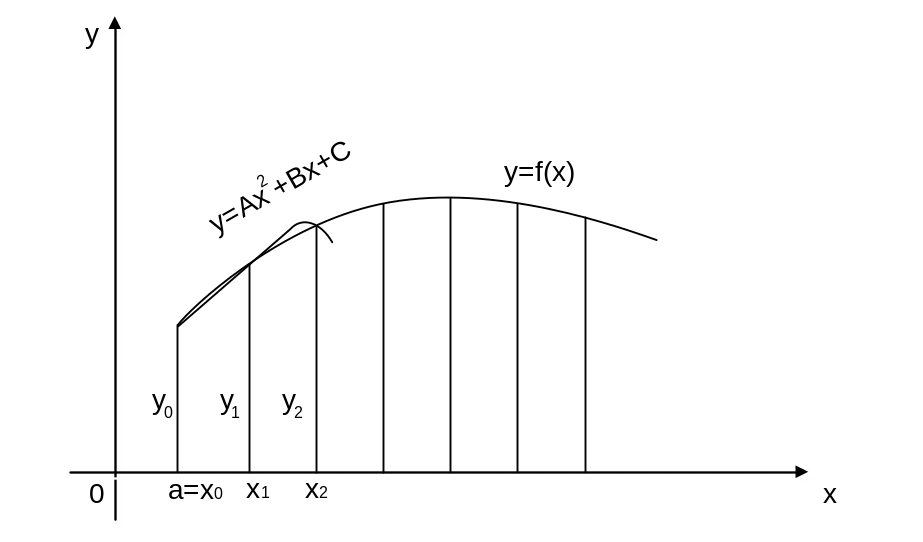
Рисунок 2.5 – Вывод формулы Симпсона

Обозначим ординаты в точках деления через y₀, y₁,...,y_n и рассмотрим пару соседних участков, например, с левым концом в точке а=х₀ (рис. 2.5). Проведем через три точки кривой с координатами (х₀, у₀), (x₁, у₁), (х₂, у₂) параболу с осью, параллельной оси Оу. Ее уравнение будет

у = Ах² + Вх + С (7)

Заменив площадь заданной криволинейной трапеции на участке [х₀, х₂] площадью криволинейной трапеции, ограниченной параболой (7), придем к приближенному равенству:

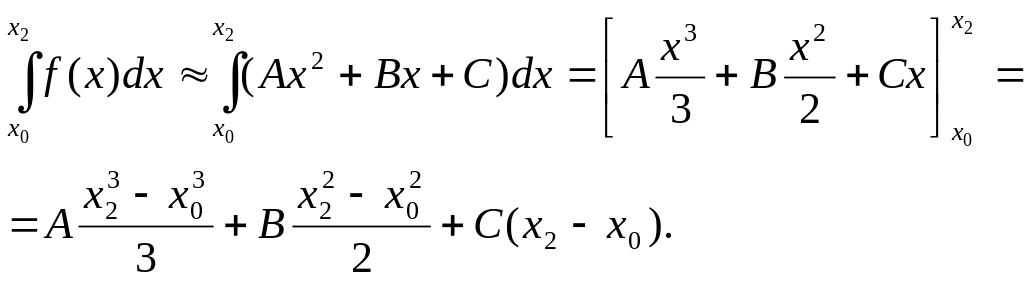
Вынося за скобку общий множитель и приводя к общему знаменателю, получим:

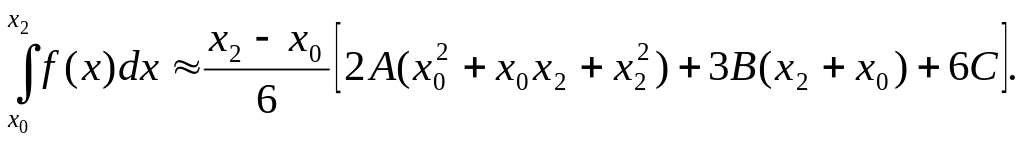(8)

Неизвестные коэффициенты А, В, С в формулах (7) и (8) находятся из условия, что при значениях х, равных х₀, х₁, х₂, функция f(x) принимает соответственно значения у₀, у₁, у₂. Заметив, что , запишем эти условия в виде

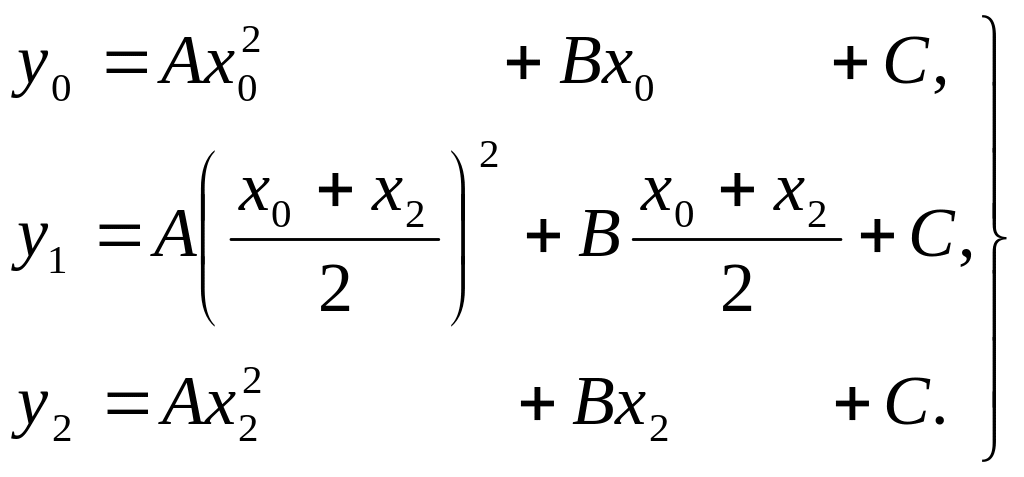(9)

Умножая второе равенство (9) на 4 и складывая после этого все три равенства (9), находим

у₀ + 4у₁ + у₂ = А[x₀² + (х₀ + х₂)² + x₂²] + В[х₀ + 2(х₀ + х₂) + х₂] + 6С =

= 2А (x₀² + х₀х₂ + x₂²) + 3B (х₀ + х₂) + 6С, (10)

что совпадает с квадратной скобкой в правой части равенства (8).

Подставив (10) в правую часть равенства (8) и заметив, что

x₂ – x₀=2h, где h = (b – a)/n, придем к приближенному равенству

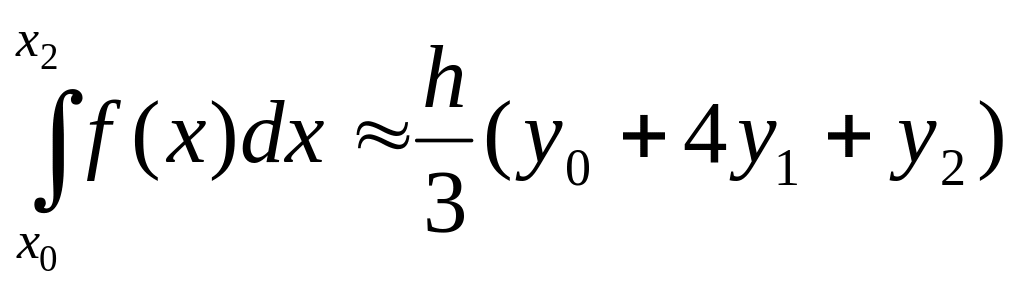. (11)

Ясно, что для каждой следующей пары участков получается такая же формула:

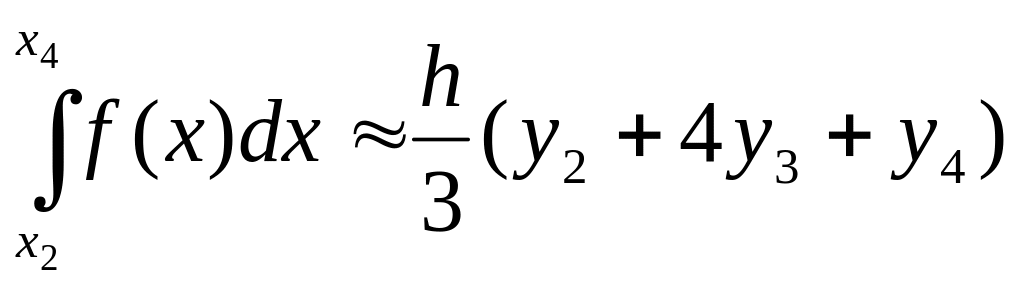(12)

Суммируя равенства вида (11) и (12) по всем участкам, получим формулу Симпсона:

(13)

Учитывая геометрический смысл формулы, ее называют также формулой парабол. В ней все ординаты с нечетными номерами умножаются на четыре, а все ординаты с четными номерами (кроме крайних) – на два. Крайние ординаты у₀ и у_2m входят в формулу с коэффициентами, равными единице.