7 Метод секущих (комбинированный метод секущих-хорд)

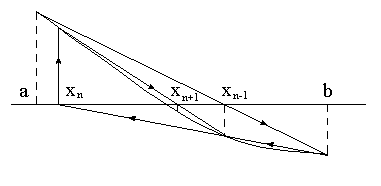
Недостаток метода Ньютона – необходимость нахождения F(x). Если это затруднено, то F(x_n) в методе Ньютона заменяется разностью последовательных значений функции, отнесенных к разности значений аргумента.

Р исунок 4.8 – Метод секущих (комбинированный метод секущих-хорд)

Этот метод (см.рис.4.8) – комбинация методов интерполяции и экстраполяции. В интерполяционной части он эквивалентен методу хорд, а в экстраполяционной – методу Ньютона.

8 Комбинированный метод касательных-хорд

С оединяя эти два метода, получаем метод (рис.4.9), на каждом этапе которого находим значения по недостатку и значения по избытку точного корня уравнения F(x) = 0.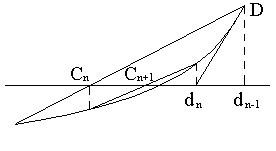

Рисунок 4.9 – Комбинированный метод касательных-хорд.

М ы считаем, что F′(x) и F′′(x) сохраняют постоянные знаки на интервале [a,b].

9 Метод последовательных приближений

Пусть необходимо найти корни уравнения

F(x) = 0.

Часто бывает удобно представить уравнение F(x) = 0 в виде

х = f(x) . (6)

Это преобразование можно выполнить различными путями. Например, если

F(x) = x² - c = 0, (7)

где c≥0, то можно к обеим частям уравнения (7) прибавить x:

(8)

или можно выражение (7) разделить на х и получить:

(9)

Наконец, можно преобразовать уравнение следующим образом:

- прибавить к обеим частям х²

- умножить обе части полученного уравнения на 1/2x, тогда

(10)

Очевидно, что значения х, являющиеся корнями, равны .

Теперь приступим к рассмотрению самого метода.

Пусть x₀ будет исходным приближённым значением корня уравнения (16). Тогда в качестве первого приближения примем

x₁ = f(x₀).

В качестве второго приближения возьмем

x₂ = f(x₁).

Продолжая этот процесс дальше, в качестве n-го приближения возьмем

x_n = f(x_n-1).

Это и есть итерационная формула рассматриваемого метода.

Основной вопрос, который нужно решить при пользовании этим методом – сходится ли x_n к решению уравнения (6) при возрастании n.

Рассмотрим сначала геометрическое представление процесса.

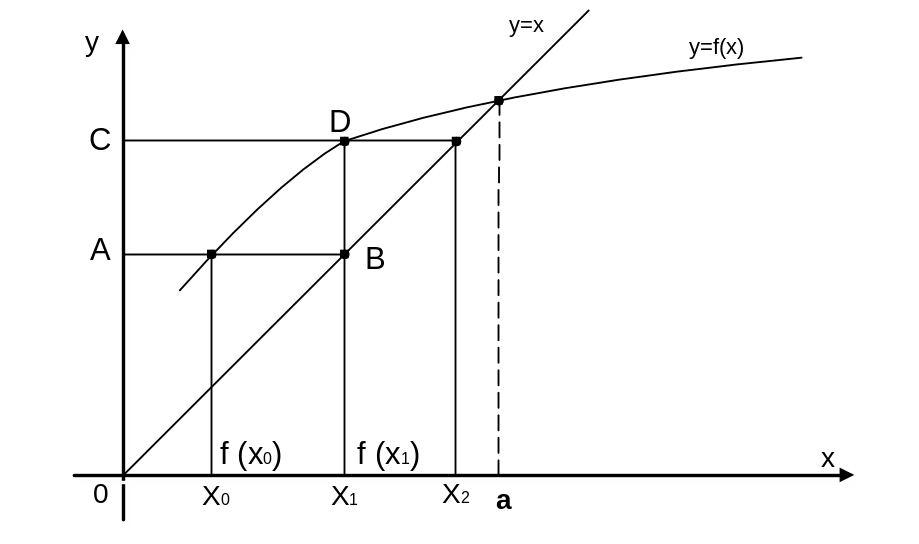
Рисунок 4.10 – Геометрическое представление итерационного процесса

При решении уравнения (6) отыскивается точка пересечения кривой y = f(x) и прямой y = x (рис.4.10). Кривая может представлять собой какую угодно функцию, но при этом должно выполняться условие сходимости итерационного процесса:

|f′(x)|<1 .

Пусть x=a – значение x в точке пересечения, тогда a является корнем этого уравнения. Но, приступая к решению задачи, мы не знаем значения корня.

Зададимся некоторым начальным приближением x_0. Значение функции в этой точке

f(x₀) = ОА .

Величину х₁ можно найти, проведя через точку А горизонтальную линию до пересечения с прямой y=x в точке В. Получим

x₁ = f(x₀)

как стороны квадрата ОАВх₁ (см. рис. 4.7).

Значение

x₂ = f(x₁)

можно найти, проведя через точку В вертикальную линию до пересечения с кривой у= f(x). При этом мы получаем отрезок ОС= f(x₁). Проведя через точку С горизонтальную линию до пересечения с прямой y=x, получаем x₂.

Процесс продолжается в том же порядке и дальше. На рис.4.10 видно, как последовательные значения х сходятся к x=a.