2 Точечная аппроксимация. Задача интерполирования

Одним из основных типов точечной аппроксимации является интерполирование. Оно состоит в следующем: для данной функции y=f(x) строят функцию (х), достаточно простую для вычислений, которая в заданных точках х₀, х₁, ..., х_n принимает значения f(x₀), f(x₁), ..., f(x_n), а в остальных точках отрезка (а, в), принадлежащего области определения f(x), приближенно представляет функцию f(x) с той или иной степенью точности. При решении задачи вместо функции f(x) оперируют с функцией (х). Задачу построения такой функции (х) называют задачей интерполирования. Точки х_i называют узлами интерполирования. Чаще всего интерполирующую функцию (х) отыскивают в виде алгебраического многочлена.

Максимальная степень интерполяционного многочлена m = n; в этом случае говорят о глобальной интерполяции, поскольку один многочлен

(x) = a₀ + a₁x + ... + a_nxⁿ (1)

используется для интерполирования функции f(x) на всем рассматриваемом интервале изменения аргумента х.

Из условия равенства значений этого многочлена в узлах x_i соответствующим заданным табличным значениям y_i получим следующую систему уравнений для нахождения коэффициентов а₀, а₁, ..., а_n:

a₀ + a₁x₀ + a₂x₀² + ... +a_nx₀ⁿ = y₀;

a₀ + a₁x₁ + a₂x₁² + ... +a_nx₁ⁿ = y₁;

- - - - - - - - - - - - - - - - - - - - - - - -

a₀ + a₁x_n + a₂x_n² + ... +a_nx_nⁿ = y_n;

Можно показать, что эта система имеет единственное решение, если среди узлов интерполяции нет совпадающих, т.е. если x_i  x_j при i  j.

Решив эту систему, найдем коэффициенты интерполяционного многочлена. Однако такой путь требует значительного объема вычислений.

Интерполяционные многочлены могут также строиться отдельно для разных частей рассматриваемого интервала изменения х. В этом случае имеем кусочную (или локальную) интерполяцию.

Как правило, интерполяционные многочлены используются для аппроксимации функции в промежуточных точках между крайними узлами интерполяции, т.е. при х₀<x<x_n. Однако они иногда используются для приближения вычисления функции вне рассматриваемого отрезка х<x₀, x>x_n. Это приближение называют экстраполяцией.

3 Интерполяционный многочлен Лагранжа

Рассмотрим более простой алгоритм построения интерполяционных многочленов.

С его помощью строится интерполяционный многочлен, единый для всего отрезка [x₀, x_n], т.е. осуществляется глобальная интерполяция. При этом, естественно, его график должен проходить через все заданные точки.

Будем искать многочлен в виде линейной комбинации многочленов степени n:

(x) = y₀Ф₀(х) + у₁Ф₁(х) + ... + у_nФ_n(х) (2)

При этом потребуем, чтобы каждый многочлен Ф_i(х) обращался в ноль при всех узлах интерполяции, за исключением одного i-го, где он должен равняться 1. Легко проверить, что этим условиям отвечает, например, многочлен вида:

(3)

Действительно, Ф₀(х) = 1 при х = х₀ При х = х₁, х₂, …, х_n числитель обращается в нуль. По аналогии получим:

(4)

- - - - - - - - - - - - - - - - - - - - - - - - - -

Подставляя в (2) выражения (3) и (4), находим :

(5)

Эта формула называется интерполяционным полиномом Лагранжа и обозначается L(x). Этот многочлен является единственным.

Из (5) можно получить выражение для линейной (n=1, рис.3.1) и квадратичной (n=2) интерполяции:

, n = 1 .

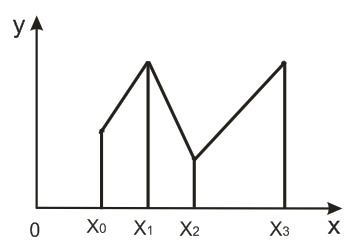
Рисунок 3.1 – Линейная интерполяция

Это – уравнение прямой

y = a₁x + b₁, x₀  x  x₁,

где

L(x) = y.

Выражение для квадратичной интерполяции:

.

Данное выражение можно привести к уравнению параболы:

y = a₁x² + b₁x + c₁.

Существует несколько обобщений интерполяционного многочлена Лагранжа. Например, широко известен интерполяционный полином Эрмита. Здесь наряду со значениями функции y_i в узлах х_i задаются значения ее производной y'_i.