1 Формула прямоугольников

Идея формулы прямоугольников заключается в том, что на малом отрезке [x₀; x₀+h] площадь криволинейной трапеции, как показано на рис.2.1, приближенно равна площади прямоугольника с основанием [x₀; x₀+h] и высотой, равной ординате в какой-то точке .

Рисунок 2.1 – Вычисление площади элементарной

криволинейной трапеции на отрезке h

Таким образом,

.

В зависимости от того, какую точку отрезка [x₀; x₀+h] выбирают в качестве , и получают разновидности формулы прямоугольников.

Разобьем отрезок [a; b] на n равных частей точками

a=x₀, x₁=x₀+h, x₂=x₁+h, … , x_i=x_i-1+h, … , x_n=x_n-1+h=b, где .

На каждом частичном отрезке [x_i-1; x_i] заменим соответствующую криволинейную трапецию на прямоугольник, высоту которого можно выбрать по-разному.

1.1 Формула «левых» прямоугольников

Если выбрать в качестве высоты прямоугольника на каждом из отрезков [x_i-1; x_i], ( ), ординату в левом конце, т. е. y_i-1=f(x_i-1), то криволинейная трапеция заменится на ступенчатую фигуру, площадь S_n которой можно принять за площадь трапеции. Верхняя граница этой ступенчатой фигуры изображена на рис. 2.2 сплошными линиями.

Рисунок 2.2 – Приближенное вычисление площади

криволинейной трапеции на отрезке [a; b]

Следовательно,

(1)

Полученную формулу называют формулой «левых» прямоугольников.

1.2 Формула «правых» прямоугольников

Если в качестве высоты прямоугольника выбрать ординату правого конца частичного отрезка, т. е. считать, что высота прямоугольника на отрезке [x_i-1; x_i] равна y_i=f(x_i), ( ), то для приближенного вычисления интеграла получим формулу «правых» прямоугольников:

(2)

(на рис. 2.2 штрихпунктирной линией обозначена ступенчатая фигура, составленная из «правых» прямоугольников).

1.3 Формула «средних» прямоугольников

Часто используется еще при расчетах так называемая формула «средних» прямоугольников или просто формула прямоугольников. Высотой прямоугольника, построенного на частичном отрезке, считают ординату, взятую в средней точке отрезка, т. е.

(получаемая ступенчатая фигура на рис. 2.2 заштрихована). Тогда

(3)

Формулы (1)—(3) можно использовать при аналитическом или графическом способе задания функции у = f (х), а формулы (1), (2) и при задании функции в виде таблицы с равноотстоящими узлами.

Формулу (3) можно записать в другом виде, более удобном для составления программ.

1.4 Случай неравноотстоящих узлов

Рассмотрим использование метода прямоугольников в случае, когда функция задана таблицей с неравноотстоящими узлами:

Таблица 1 – Задание функции с неравноотстоящими узлами

i	0	1	2	…	i	…	n
xi	a=x0	x1	x2	…	xi	…	xn=b
yi	y0	y1	y2	…	yi	…	yn

Обозначим h₁=x_l - x₀, h₂=x₂ – x₁, ..., h_i=x_i - x_i-1, ... ,h_n = x_n – х_n-1, причем не все h_i, ( ), равны между собой. Для вычисления определенного интеграла по методу прямоугольников в этом случае легко получить формулы (1.1) и (2.1), аналогичные формулам (1) и (2):

(1.1)

— формула «левых» прямоугольников;

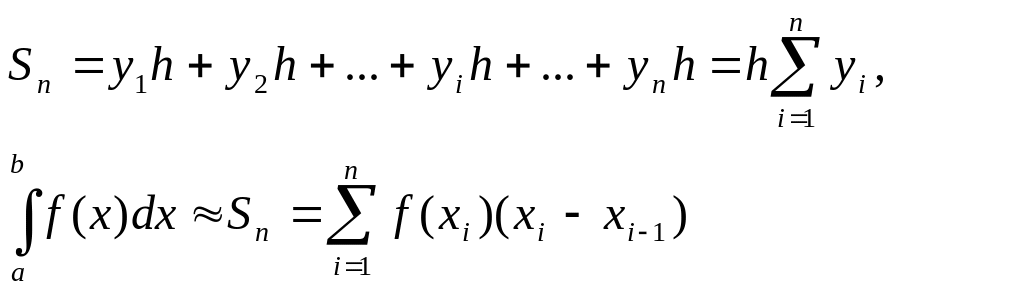(2.1)

— формула «правых» прямоугольников.