8.6. Непрерывность и разрывы монотонной функции

Рассмотрим функцию f (x), которая, – при изменении х в промежутке Р – монотонно возрастает (убывает) хотя бы в широком смысле (гл.1, §4, п.4.4). По отношению к таким функциям имеет место следующая теорема.

Теорема 1. Монотонно убывающая (возрастающая) функция f(x) может иметь в Р разве лишь разрывы первого рода, т.е. скачки.

Возьмем любую точку х₀ промежутка Р, и пусть она не является левым концом этого промежутка. Рассматривая ту часть промежутка, которая лежит влево от х₀, применим к ней теорему 12 из §6, п.6.3 о пределе монотонной функции: поскольку для х < х₀, очевидно, f (x) ≤  f (x₀), то существует конечный предел .

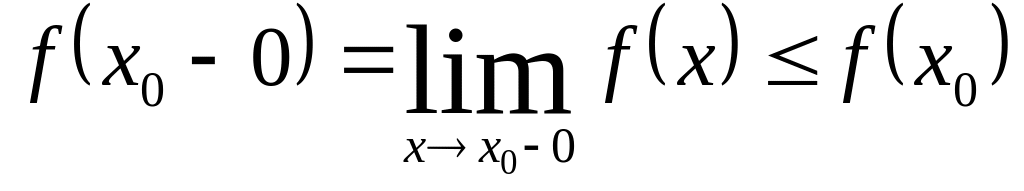Если он совпадает со значением f (x₀), то слева в точке х₀ функция непрерывна; в противном случае – налицо скачок.

Аналогично убеждаемся в том, что в каждой точке х₀ промежутка Р (не служащей правым его концом) справа тоже либо имеет место непрерывность, либо скачок.

С помощью доказанной теоремы легко установить критерий непрерывности монотонной функции.

Теорема 2. Если значения монотонно возрастающей (убывающей) в промежутке Р функции f (x) содержатся в промежутке Е и сплошь заполняют его (так что каждое значение у из Е принимается функцией хоть раз), то эта функция непрерывна в Р.

Допустим, что в какой-нибудь точке х₀ из Р функция f (x) имеет разрыв, например, слева; как мы видели, этот разрыв может быть только скачком. В этом случае существует предел f (x₀ – 0), но он меньше значения f (x₀). Так как для будет а для очевидно, то функция не может принимать значений у, лежащих между числами и f (x₀), принадлежащих промежутку Е. Это противоречит условию теоремы; значит, функция разрывов не имеет.

8.7. Непрерывность сложной функции

Теорема. Пусть функция  (у) определена в промежутке Е, а функция f (х) – в промежутке Р, причем значения последней функции не выходят за пределы Е, когда х изменяется в Р. Если f (х) непрерывна в точке х₀ из Р, а  (у) непрерывна в соответствующей точке у₀ = f (х₀) из Е, то и сложная функция  [f (х)] будет непрерывна в точке х₀.

Доказательство. Зададимся произвольным числом > 0. Так как  (у) непрерывна при у = у₀, то по найдется такое  > 0, что из у – у₀   следует

 (у) –  (у₀)  .

С другой стороны, ввиду непрерывности f (x) при х = х₀, по  найдется такое   > 0, что из х – х₀   следует f (x) – f (x₀) =  у –у₀   .

По самому выбору числа  отсюда следует далее

.

Этим "на языке " и доказана непрерывность функции в точке х₀.

8.8. Непрерывность элементарных функций

Прежде рассмотрим основные элементарные функции, непрерывность которых можно установить, пользуясь теоремой 2 (гл.1, §8, п.8.6).

1. Показательная функция. Функция у = а^х либо монотонно возрастает (а > 1), либо монотонно убывает (0 < а < 1) при изменении х в промежутке Р = (–∞,+∞). Ее значения положительны и заполняют весь промежуток Е = (0,+∞), что видно из существования логарифма x = log_a y для любого y > 0. Следовательно, показательная функция непрерывна при любом значении х.

2. Логарифмическая функция у = log_a х (а > 0, а  1). Ограничиваясь случаем а > 1, видим, что эта функция возрастает при изменении х в промежутке Р = (0,+∞). К тому же она, очевидно, принимает любое значение у из промежутка Е = (–∞, +∞), именно, для х = а^у. Отсюда ее непрерывность.

3. Степенная функция у = х^ при возрастании х от 0 до + возрастает, если   0, и убывает, если   0. При этом она принимает любое положительное значение у , следовательно, и она непрерывна. Отметим, что если   0, то значение 0 включается как в промежуток изменения х, так и в промежуток изменения у; при   0 значение 0 не включается. Далее, если  – целое число п или дробное с нечетным знаменателем, то степень х^ можно рассматривать и для х  0; непрерывность ее для этих значений устанавливается аналогично.

4. Тригонометрические функции. Остановимся сначала на функции sin х. Непрерывность функции y = sin x, скажем, при изменении в промежутке , вытекает из ее монотонности в этом промежутке (гл.1, §4, п.4.4), да еще из того факта (устанавливаемого геометрически), что при этом она принимает каждое значение между –1 и +1. То же относится и к любому промежутку вида

, где k = 0, ±1, ±2, ....

Аналогично устанавливается и непрерывность функции cos x при любом значении х.

Отсюда, по теореме (гл.1, §8, п.8.5) вытекает непрерывность функций

.

Исключение представляют для первых двух – значения вида , обращающие cos x в 0, а для последних двух – значения вида k, обращающие sin x в 0.

5. Обратные тригонометрические функции: у = arcsin x, у = arcсоs x, у = arctg x, у = arcсtg x. Первые две непрерывны в промежутке [–1,+1], а последние – в промежутке (–, +). Доказательство предоставляем провести самостоятельно.

Резюмируя, можно, таким образом, сказать, что основные элементарные функции оказываются непрерывными во всех точках, где они имеют смысл (т.е. в соответствующих естественных областях их определения).

Исходя из этого, теперь, на основании теорем (гл.1, §8, п.8.5) и (гл.1, §8, п.8.7), мы можем заключить, что и все элементарные функции, построенные из непрерывных основных элементарных функций, также будут непрерывны.