
- •Министерство образования и науки украины одесский национальный университет имени и.И. Мечникова институт инновационного и последипломного образования
- •Глава 1 числовые функции одного действительного переменного
- •§1. Область определения функции
- •Ограниченные числовые множества
- •1.2. Числовые промежутки. Окрестность точки
- •1.3. Предельные точки множества
- •§ 2. Способы задания функции
- •2.1. Табличный способ задания функции
- •2.2. Графический способ задания функции
- •2.3. Аналитический способ задания функции
- •2.4. Неявное задание функции. Алгебраические и трансцендентные функции
- •2.5. Параметрическое задание функции
- •§3. Обратная функция для аналитически заданной функции
- •§4. Элементарные функции и их классификация
- •4.1. Основные (простейшие) элементарные функции
- •4.2. Элементарные функции
- •4.3. Ограниченные функции
- •Если f(p) является ограниченным (или неограниченным) множеством, то говорят, что функция f(X) ограничена (или неограничена).
- •4.4. Монотонные функции
- •4.5. Четные и нечетные функции
- •4.6. Периодические функции
- •§5. Предел числовой последовательности
- •5.1. Определение и геометрическое истолкование предела последовательности
- •Постоянная последовательность {yn} имеет пределом число и является сходящейся последовательностью.
- •5.2. Некоторые теоремы о последовательностях, имеющих предел
- •5.3. Бесконечно малые последовательности и их свойства
- •5.4. Бесконечно большие последовательности и их свойства
- •5.5. Арифметические операции над последовательностями, имеющими предел
- •5.6. Неопределенные арифметические выражения
- •5.7. Неопределенные степенно-показательные выражения
- •5.8. Монотонные последовательности
- •5.9. Принцип сходимости последовательности
- •Упражнения
- •§6. Предел числовой функции одного действительного переменного
- •6.1. Определение и геометрическое истолкование предела функции
- •6.2. Односторонние и бесконечные пределы функции
- •6.3. Распространение теории пределов
- •6.4. Примеры на нахождение пределов для некоторых неопределенных выражений
- •§7. Классификация бесконечно малых и бесконечно больших функций одного действительного переменного
- •7.1. Сравнение бесконечно малых
- •Наоборот, бесконечно малые
- •Будут, очевидно, высшего порядка, чем х.
- •7.2. Классификация бесконечно больших
- •Упражнения
- •§8. Непрерывность (и разрывы) функции одного действительного переменного
- •8.1. Определение непрерывности функции в точке
- •8.2. Односторонняя непрерывность функции в точке. Функции, непрерывные в промежутке
- •8.3. Равномерная непрерывность
- •8.4. Разрывы функции. Классификация разрывов
- •Например, рассмотрим функцию
- •8.5. Арифметические операции над непрерывными функциями
- •8.6. Непрерывность и разрывы монотонной функции
- •8.7. Непрерывность сложной функции
- •8.8. Непрерывность элементарных функций
- •8.9. Общие свойства непрерывных функций
- •Упражнения
6.4. Примеры на нахождение пределов для некоторых неопределенных выражений
1.
Пусть функция f (х)
= α0
+ α1х
+ . . . + αnхn
есть многочлен.
Применяя утверждения 8 и 9 (§6, п.6.3), а
также результаты примера §6, п.6.1, получим

![]()
Если х0 является бесконечно удаленной предельной точкой, то
 ∞
∞
как произведение бесконечно большой величины на ограниченную величину (в круглых скобках все слагаемые, кроме αn 0, при х ∞ бесконечно малые).
2.
Пусть функция
 дробно-рациональная. Тогда, используя
результаты примера, приведенного выше
и утверждение 10 (§6,
п.6.3),
предполагая, что х0
не есть корень
знаменателя, получим
дробно-рациональная. Тогда, используя
результаты примера, приведенного выше
и утверждение 10 (§6,
п.6.3),
предполагая, что х0
не есть корень
знаменателя, получим

Если
х0
есть корень знаменателя, но не является
корнем числителя, то
 ∞,
как отношение ограниченной величины,
отличной от нуля, на бесконечно малую.
∞,
как отношение ограниченной величины,
отличной от нуля, на бесконечно малую.
Если
же х0
является
корнем и числителя, и знаменателя, то
имеет место особый случай, обозначаемый
как
![]() .
.
В этом случае многочлены числителя и знаменателя, согласно теоремы Безу (книга 2, гл. 3, §4), делятся на х – х0 без остатка и следовательно их можно представить в виде

Отсюда, сократив числитель и знаменатель на общий множитель х – х0 получаем

В зависимости от кратности корня х0 эту операцию повторяем до тех пор пока х0 не будет одновременно корнем и числителя, и знаменателя, и тем самым мы не придем к одному из случаев рассмотренных выше.
Теперь найдем предел дробно-рациональной функции при условии, что х ∞. Рассмотрим следующие случаи.
а)
Пусть n
>
m.
Тогда, разделив числитель и знаменатель
на xm,
находим
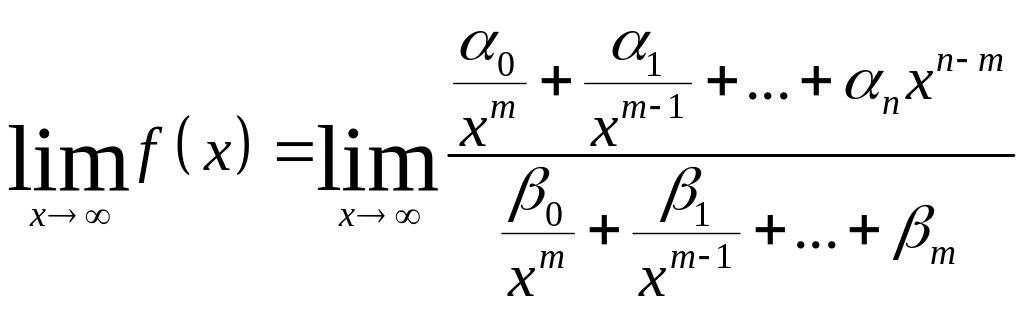 .
.
Если
теперь перейти к пределу в каждом
слагаемом числителя и знаменателя, то
в числителе получим бесконечность, а в
знаменателе – число m,
т.е.
![]() .
.
б) Пусть п = т. Тогда, после деления числителя и знаменателя на хт = хп, получаем
 .
.
в) Пусть n < m. Тогда, после деления числителя и знаменателя на xn, получаем:
 ,
,
поскольку n есть конечное число, отличное от нуля, а в знаменателе бесконечно большая величина.
Таким образом,
 .
.
3.
Вычисление предела для иррациональных
функций в особых случаях, характеризуемых
символами
![]() выполняется, в основном, при помощи:
выполняется, в основном, при помощи:
а)
умножения функции f (x)
на такую функцию (x),
которая
позволяет устранить неопределенность
и предел которой равен единице. Например,
вычислить предел функции
![]() при х
.
Умножим функцию f (x)
на функцию
при х
.
Умножим функцию f (x)
на функцию
![]() ,
предел которой при х
равен единице.
Тогда
,
предел которой при х
равен единице.
Тогда

б) использования формул:
![]() (1.20)
(1.20)
 .
(1.21)
.
(1.21)
Например,
вычислить
 Разделим числитель и знаменатель на х
и с использованием (1.20) находим
Разделим числитель и знаменатель на х
и с использованием (1.20) находим
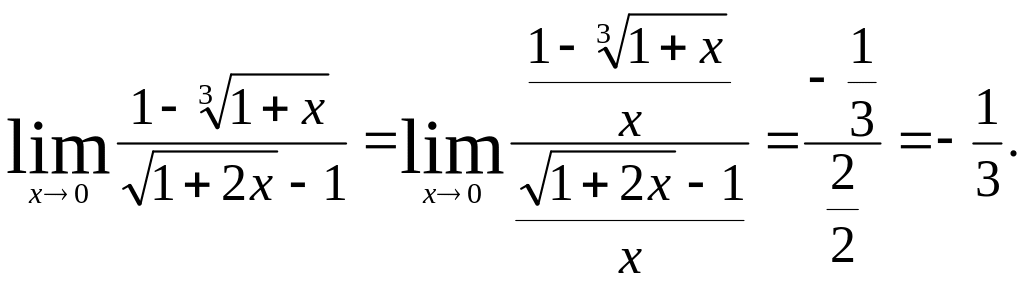
4. При вычислении предела неопределенных выражений, содержащих тригонометрические функции, руководствуются, в основном, следующими соображениями и формулами:
а)
функции
![]() и
и
![]() при стремлении х
к ∞
ограничены и
предела не имеют. На основание этого
при стремлении х
к ∞
ограничены и
предела не имеют. На основание этого
![]()
б)
функция
![]() при стремлении х
к
при стремлении х
к
![]() ,
m
= 0, 1,
2...
бесконечно большая, т.е.
,
m
= 0, 1,
2...
бесконечно большая, т.е.

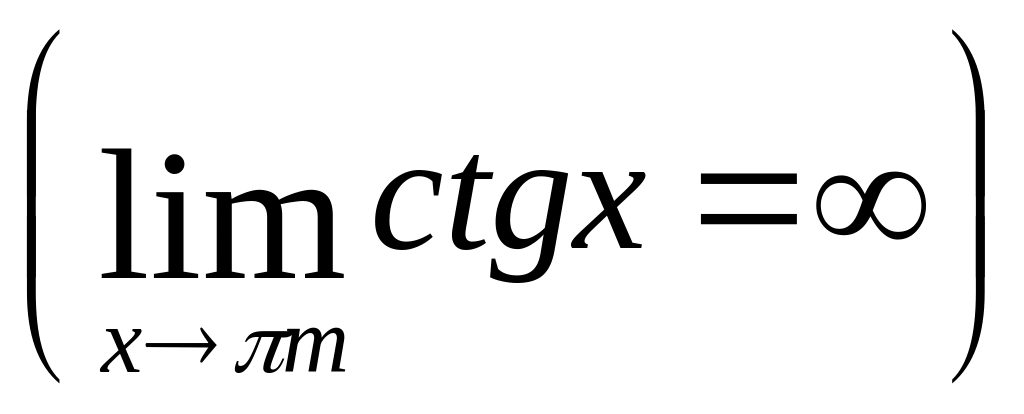 .
.
При
![]() ∞, хотя функции
∞, хотя функции
![]() неограниченны,
однако предела они не имеют и не являются
бесконечно большими. Действительно для
этих функций нельзя подобрать такое
число
0,
чтобы неравенство f(х)
>
выполнялось бы для всех х
;
неограниченны,
однако предела они не имеют и не являются
бесконечно большими. Действительно для
этих функций нельзя подобрать такое
число
0,
чтобы неравенство f(х)
>
выполнялось бы для всех х
;
в)
![]() и
и
![]()
г)
если
 и
и
![]() при
при
![]() то
то

Например,
вычислить
![]() Сначала преобразуем функцию
Сначала преобразуем функцию
 .
.
Теперь с учетом в) и г) получаем
 .
.
5. Нахождение предела неопределенных степенно-показательных выражений, а также выражений, в которые входят показательные и логарифмические функции, в некоторых случаях удается провести при помощи следующих формул:
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
Например,
вычислить
![]()
Преобразуем функцию, разделив числитель и знаменатель на х – 5. Получим

Теперь с учетом вышеприведенных формул, находим


