
- •Министерство образования и науки украины одесский национальный университет имени и.И. Мечникова институт инновационного и последипломного образования
- •Глава 1 числовые функции одного действительного переменного
- •§1. Область определения функции
- •Ограниченные числовые множества
- •1.2. Числовые промежутки. Окрестность точки
- •1.3. Предельные точки множества
- •§ 2. Способы задания функции
- •2.1. Табличный способ задания функции
- •2.2. Графический способ задания функции
- •2.3. Аналитический способ задания функции
- •2.4. Неявное задание функции. Алгебраические и трансцендентные функции
- •2.5. Параметрическое задание функции
- •§3. Обратная функция для аналитически заданной функции
- •§4. Элементарные функции и их классификация
- •4.1. Основные (простейшие) элементарные функции
- •4.2. Элементарные функции
- •4.3. Ограниченные функции
- •Если f(p) является ограниченным (или неограниченным) множеством, то говорят, что функция f(X) ограничена (или неограничена).
- •4.4. Монотонные функции
- •4.5. Четные и нечетные функции
- •4.6. Периодические функции
- •§5. Предел числовой последовательности
- •5.1. Определение и геометрическое истолкование предела последовательности
- •Постоянная последовательность {yn} имеет пределом число и является сходящейся последовательностью.
- •5.2. Некоторые теоремы о последовательностях, имеющих предел
- •5.3. Бесконечно малые последовательности и их свойства
- •5.4. Бесконечно большие последовательности и их свойства
- •5.5. Арифметические операции над последовательностями, имеющими предел
- •5.6. Неопределенные арифметические выражения
- •5.7. Неопределенные степенно-показательные выражения
- •5.8. Монотонные последовательности
- •5.9. Принцип сходимости последовательности
- •Упражнения
- •§6. Предел числовой функции одного действительного переменного
- •6.1. Определение и геометрическое истолкование предела функции
- •6.2. Односторонние и бесконечные пределы функции
- •6.3. Распространение теории пределов
- •6.4. Примеры на нахождение пределов для некоторых неопределенных выражений
- •§7. Классификация бесконечно малых и бесконечно больших функций одного действительного переменного
- •7.1. Сравнение бесконечно малых
- •Наоборот, бесконечно малые
- •Будут, очевидно, высшего порядка, чем х.
- •7.2. Классификация бесконечно больших
- •Упражнения
- •§8. Непрерывность (и разрывы) функции одного действительного переменного
- •8.1. Определение непрерывности функции в точке
- •8.2. Односторонняя непрерывность функции в точке. Функции, непрерывные в промежутке
- •8.3. Равномерная непрерывность
- •8.4. Разрывы функции. Классификация разрывов
- •Например, рассмотрим функцию
- •8.5. Арифметические операции над непрерывными функциями
- •8.6. Непрерывность и разрывы монотонной функции
- •8.7. Непрерывность сложной функции
- •8.8. Непрерывность элементарных функций
- •8.9. Общие свойства непрерывных функций
- •Упражнения
5.5. Арифметические операции над последовательностями, имеющими предел
Теорема 1 (о пределе суммы (разности)). Если последовательности {yn} и {хn} имеют конечные пределы: lim yn = , lim хn = , то и последовательности {yn ± xn} также имеют конечный предел, причем
![]() .
.
Доказательство. Из условия теоремы следует, что yn = un, xn = + vn, где последовательности {un} и {vn} – бесконечно малые. Тогда yn ± xn = ( ) + + (un vn).
Здесь последовательности {un vn} есть бесконечно малые по теореме 1 (п.5.3); следовательно, пользуясь вторым определением предела, можно утверждать, что последовательности {yn ± xn} имеют пределы, равные , что и требовалось доказать. Эта теорема и ее доказательство переносятся на случай любого конечного числа слагаемых.
Теорема 2 (о пределе произведения). Если последовательности {yn} и {хn} имеют конечные пределы: lim yn = , lim хn = , то и последовательность {yn xn} также имеет конечный предел и lim {yn ·xn} = lim yn·lim хn = ·.
Доказательство аналогично доказательству теоремы 1.
Теорема обобщается на случай конечного числа сомножителей.
Следствие. Постоянный множитель можно выносить за знак предела:
lim yn = lim yn , где постоянное число.
Действительно,
если последовательность постоянная
![]() = {},
то ее предел lim
хn
= .
Тогда по теореме 2: lim
{yn
·
xn}
= lim
yn·lim
хn=
lim
yn.
= {},
то ее предел lim
хn
= .
Тогда по теореме 2: lim
{yn
·
xn}
= lim
yn·lim
хn=
lim
yn.
Теорема
3
(о
пределе частного).
Если
последовательности {yn}
и {хn}
имеют конечные пределы: lim
yn
=
,
lim хn
= ,
то и последовательность
![]() также имеет конечный предел, а именно
также имеет конечный предел, а именно
![]() .
.
Доказательство. Из условий yn и xn имеем yn = + un и xn = + vn, где последовательности {un} и {vn} – бесконечно малые. Тогда
![]() .
.
По
свойствам бесконечно малых последовательность
![]() есть бесконечно малая. Тогда и
последовательность
есть бесконечно малая. Тогда и
последовательность
![]() также бесконечно малая, как произведение
ограниченной последовательности
также бесконечно малая, как произведение
ограниченной последовательности
![]() на бесконечно малую. Таким образом, по
второму определению предела следует,
что
на бесконечно малую. Таким образом, по
второму определению предела следует,
что
![]() или
или
![]() .
.
5.6. Неопределенные арифметические выражения
В предыдущем разделе мы установили пределы последовательностей, которые определялись арифметическими выражениями
![]()
![]()
![]() (1.10)
(1.10)
и,
в предположении, что последовательности
![]() и
и
![]() стремятся к конечным пределам (из
которых, в случае частного, xn
и предел
не должны были равняться нулю).
стремятся к конечным пределам (из
которых, в случае частного, xn
и предел
не должны были равняться нулю).
Остановимся теперь на случаях, когда пределы последовательностей и будут (один или оба) бесконечными или – если речь идет о частном – когда предел знаменателя будет нулем.
Начнем рассмотрение именно с частного:
1)
Если
имеет
конечный предел, а
стремится к ∞,
то
![]() стремится к нулю.
стремится к нулю.
В
самом деле,
![]() ;
так как второй множитель есть бесконечно
малая (как обратная бесконечно большой),
то, по теореме 2 (п.5.3), и
;
так как второй множитель есть бесконечно
малая (как обратная бесконечно большой),
то, по теореме 2 (п.5.3), и
![]() есть также бесконечно малая.
есть также бесконечно малая.
2)
Если
имеет
предел, конечный или нет, а
xn 0,
то
![]() ∞.
∞.
Имеем
 .
К последовательности
.
К последовательности
![]() применима теорема
3 о пределе
частного – она стремится к нулю.
Следовательно, последовательность
применима теорема
3 о пределе
частного – она стремится к нулю.
Следовательно, последовательность
![]()
![]() (как
обратная бесконечно малой) имеет пределом
∞.
(как
обратная бесконечно малой) имеет пределом
∞.
3)
Если yn→∞,
а
![]() имеет
конечный предел, то
имеет
конечный предел, то
![]() .
.
Действительно,
так
как
![]() в силу 1) стремится к нулю, то
в силу 1) стремится к нулю, то
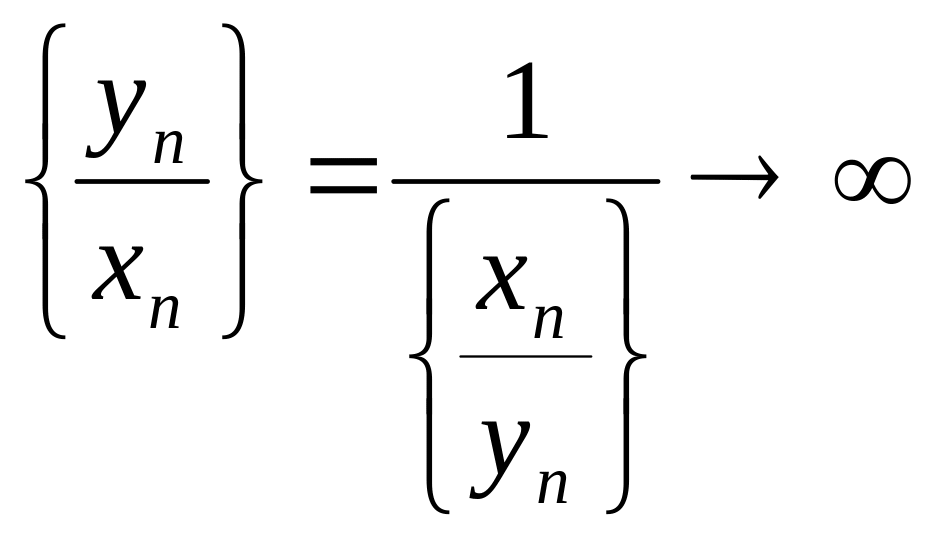 .
.
Теперь переходим к случаю, когда обе последовательности
 и
одновременно стремятся к нулю. В этом
случае никакого общего заключения о
пределе последовательности
мы сделать не можем. Этот предел, в
зависимости от закона изменения обеих
последовательностей, может иметь
различные значения или даже вовсе не
существовать. Поясним это на примерах.
и
одновременно стремятся к нулю. В этом
случае никакого общего заключения о
пределе последовательности
мы сделать не можем. Этот предел, в
зависимости от закона изменения обеих
последовательностей, может иметь
различные значения или даже вовсе не
существовать. Поясним это на примерах.
Пусть
![]() ,
и
,
и
![]() ;
обе последовательности стремятся к
нулю. Их отношение
;
обе последовательности стремятся к
нулю. Их отношение
![]() также стремится к нулю. Если же, наоборот,
положить
также стремится к нулю. Если же, наоборот,
положить
![]() ,
,
![]() ,
то, хотя они по прежнему стремятся к
нулю, на этот раз их отношение
,
то, хотя они по прежнему стремятся к
нулю, на этот раз их отношение
![]() стремится к ∞
Взяв же любое отличное от нуля число
и построив две бесконечно малые
стремится к ∞
Взяв же любое отличное от нуля число
и построив две бесконечно малые
![]() и
,
видим, что отношение их имеет пределом
(так
как
тождественно равно ).
и
,
видим, что отношение их имеет пределом
(так
как
тождественно равно ).
Наконец,
если
![]() ,
(обе имеют пределом нуль), то отношение
,
(обе имеют пределом нуль), то отношение
![]() оказывается вовсе не имеющим предела.
оказывается вовсе не имеющим предела.
Таким
образом, одно знание пределов
последовательностей
и
в данном случае не позволяет еще судить
о поведении их отношения,
необходимо
знать также закон их изменения. Для
того, чтобы характеризовать эту
особенность случая, когда yn
0 и xn
0,
говорят, что
выражение
представляет неопределенность
–
вида
![]() .
.
5) В случае, когда одновременно yn ∞ и xn ∞, имеет место подобное же обстоятельство. Не зная самих последовательностей, общего утверждения о поведении их отношения сделать нельзя. Проиллюстрируем это на примерах:
yn
= n
∞,
xn
= n2
∞,
=![]() 0;
0;
yn
= n2
∞, xn
=
n
∞,
=
![]() ∞;
∞;
yn
= ·n
∞ ( ,
xn
= n
∞,
![]() ;
;
yn
= (1)n·n
∞,
xn
= n
∞,
![]() вовсе
не имеет
предела.
вовсе
не имеет
предела.
И
в этом случае говорят, что выражение
представляет неопределенность
–
вида
![]() .
.
Обратимся
к рассмотрению произведения
![]() :
:
6) Если имеет предел, конечный или нет, но не равный нулю, а xn ∞, то ∞.
В
самом деле, последовательность
![]() есть бесконечно малая (так
как
первый множитель имеет конечный предел,
а второй стремится к нулю); отсюда и
вытекает требуемое заключение.
есть бесконечно малая (так
как
первый множитель имеет конечный предел,
а второй стремится к нулю); отсюда и
вытекает требуемое заключение.
7)
Если уn 0,
в то время как xn
∞, то исследуя
поведение произведения
![]() мы сталкиваемся с такой же особенностью,
как и в пунктах 4) и 5). Об этом свидетельствуют
примеры:
мы сталкиваемся с такой же особенностью,
как и в пунктах 4) и 5). Об этом свидетельствуют
примеры:
![]()
![]()
![]()
![]() ,
вовсе не имеет предела.
,
вовсе не имеет предела.
В
связи с этим при
![]() и
и
![]() ,
говорят, что выражение
,
говорят, что выражение
![]() представляет неопределенность
вида 0·.
представляет неопределенность
вида 0·.
Рассмотрим,
наконец, алгебраическую сумму
![]() :
:
8)
если
![]() ∞,
а
∞,
а
![]() имеет
конечный предел, то
имеет
конечный предел, то
![]() ∞.
∞.
9)
Если
![]() и
и
![]() обе стремятся к +∞
(или обе к –∞),
то к тому же пределу стремится и сумма
обе стремятся к +∞
(или обе к –∞),
то к тому же пределу стремится и сумма
![]() .
.
Доказательство 8) и 9) предлагаем провести самостоятельно.
10) Случай же, когда и стемятся к бесконечности разных знаков, снова оказывается особым: о сумме ничего определенного сказать нельзя, не зная самих последовательностей и .
Примеры.
![]()
![]()
![]()
![]() – предела
не имеет.
– предела
не имеет.
Ввиду
этого, при
![]() говорят, что выражение
говорят, что выражение
![]() представляет неопределенность
вида ∞
– ∞.
представляет неопределенность
вида ∞
– ∞.
