ЛЕКЦИЯ №1.
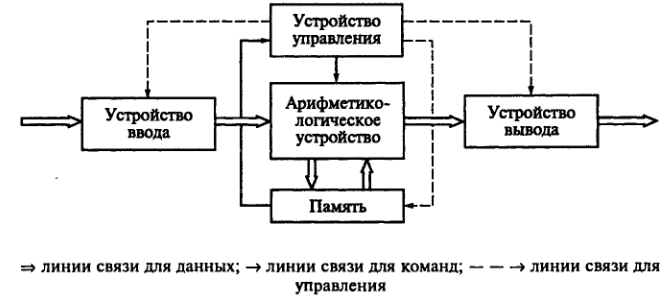Рис.2.
Структура ЭВМ фон Неймана
Организация вычислительного процесса
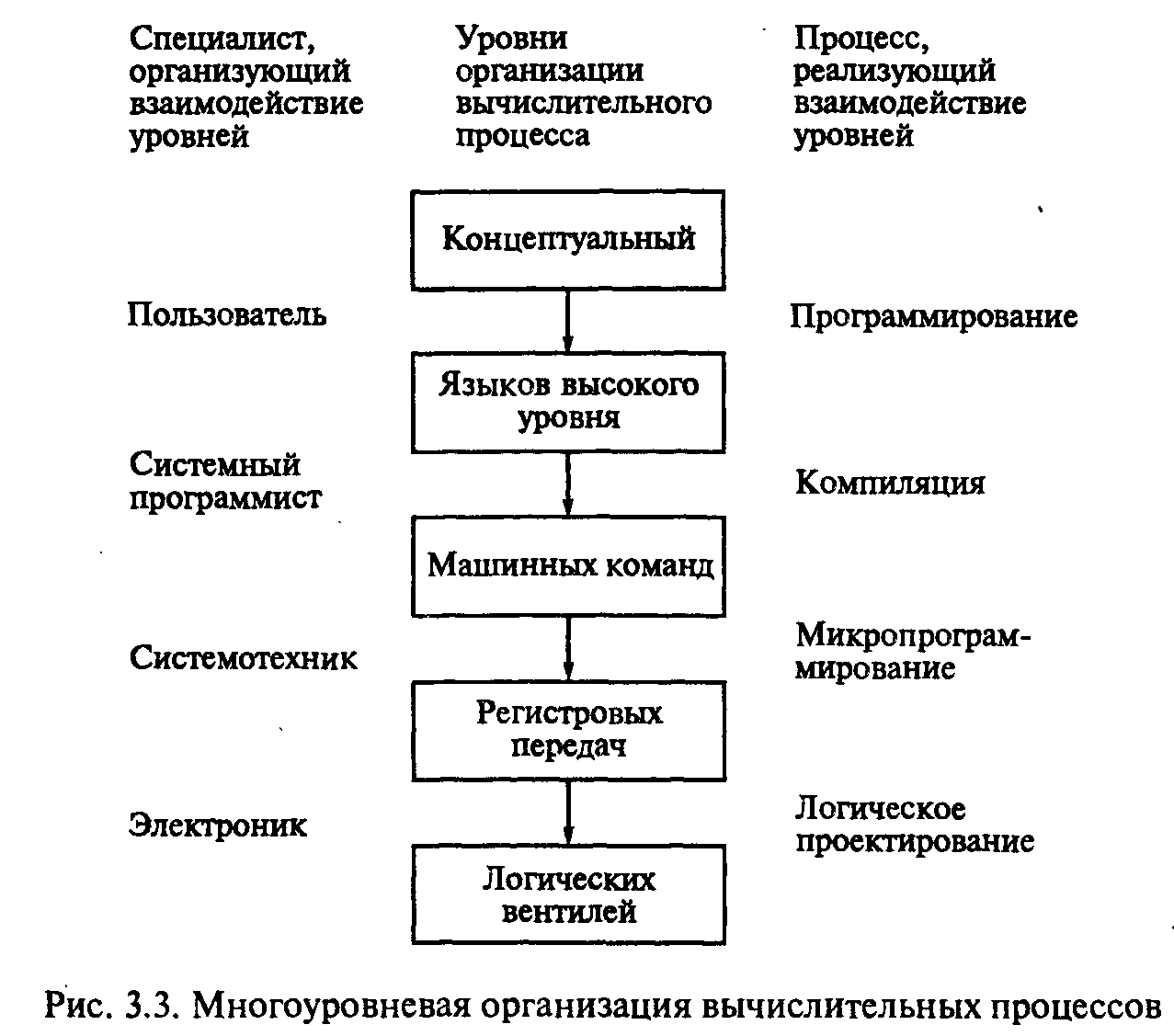
Аппаратные и программные средства эвм
ЛЕКЦИЯ №2
Представление информации в ЭВМ. Системы счисления.
Система счисления (СС) — совокупность приёмов и правил изображения чисел цифровыми знаками. Системы счисления делятся на непозиционные и позиционные.
Непозиционная система счисления — система, в которой, значение символа не зависит от его положения в числе. Непозиционные системы счисления возникли раньше позиционных систем. Они использовались в древности римлянами, египтянами, славянами и другими народами. Примером непозиционной системы счисления, дошедшей до наших дней, служит римская система счисления. Цифры в римской системе обозначаются различными знаками: 1—I; 3—III; 5—V; 10—X; 50—L; 100—C; 500—D; 1000—M. Для записи промежуточных значений существует правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а слева — вычитается из него. Так, IV обозначает 4, VI—6, LX—60, XC—90 и т.д. Основной недостаток непозиционных систем — большое число различных знаков и сложность выполнения арифметических операций.
Позиционная система счисления — система, в которой значение символа зависит от его места в ряду цифр, изображающих число. Например, в числе 7382 первая цифра слева означает количество тысяч, вторая — количество сотен, третья — количество десятков и четвёртая количество единиц. Позиционные системы счисления (ПСС) более удобны для вычислительных операций, поэтому они получили более широкое распространение.
Позиционная система счисления характеризуется основанием m. Эту величину, указывающую число различных символов в коде, называют также позиционностью кода. В зависимости от значения основания m коды называются двоичными (m=2), троичными (m=3), десятеричными (m=10), шестнадцатеричными (m=16) и т.д.
Для любой натуральной системы счисления любое число N в пределах объема цифрового кода можно записать в виде значений коэффициентов ki ряда
,
где n – число разрядов кода; k может меняться от 0 до m–1.
Во всех современных ЭВМ для представления числовой информации используется двоичная система счисления. Это обусловлено:
• более простой реализацией алгоритмов выполнения арифметических и логических операций;
• более надежной физической реализацией основных функций, так как они имеют всего два состояния (0 и 1);
• экономичностью аппаратной реализации всех схем ЭВМ.
При m=2 число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (0 и 1).
Для двоичной системы счисления:
.
Так, например, число 26 запишется следующим образом: 26 = 1*24 + 1*23 + 0*22 + +1*21+0*20 = 16 + 8 + 2, т.е. 11010.
Кроме двоичной системы счисления широкое распространение получили и производные системы:
Десятичная СС — {0, 1, .... 9}.
Для десятичной системы (m=10):
.
Примеры: 7264 = 7*103 + 2*102 + 6*101 + 4*100. (число 7204 равно семи тысячам плюс две сотни плюс шесть десятка плюс четыре единицы (7000+200 + 60+4=7264).
4627.31=4*103+6*102+2*101+7*100+3*10-1+1*10-2.
Шестнадцатеричная СС — {0, 1, 2,..., 9, А, В, С, D, Е, F}.
Восьмеричная СС — {0, 1, 2, 3, 4, 5, 6, 7}. Она широко используется во многих специализированных ЭВМ.
Восьмеричная и шестнадцатеричная системы счисления являются производными от двоичной, так как 16 = 24 и 8 = 23. Они используются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков.
Рассмотрим обозначения первых 16 целых чисел в различных СС:
Таблица 3. Десятичная, шестнадцатеричная и двоичная системы счисления
Десятичная |
Шестнадцатеричная |
Двоичная |
Восьмеричная |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
2 |
10 |
2 |
3 |
3 |
11 |
3 |
4 |
4 |
100 |
4 |
5 |
5 |
101 |
5 |
6 |
6 |
110 |
6 |
7 |
7 |
111 |
7 |
8 |
8 |
1000 |
0 |
9 |
9 |
1001 |
1 |
10 |
А |
1010 |
2 |
11 |
В |
1011 |
3 |
12 |
С |
1100 |
4 |
13 |
D |
1101 |
5 |
14 |
Е |
1110 |
6 |
15 |
F |
1111 |
7 |