7. Інтегральна формула Коші.

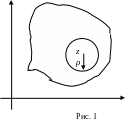
Теорема 1. Нехай межа обмеженої області складається із скінченного числа замкнених спрямованих жорданових кривих, а функція голоморфна в і неперервна в . Тоді

 , , (1)

, . (2)

Доведення. Якщо , то функція голоморфна в і неперервна в . Тому із теореми Коші отримуємо (2). Нехай і настільки мале, що . Тоді за теоремою Коші, застосованою до області , маємо

,

тобто

. (3)

Враховуючи, що

,

маємо

. (4)

Оскільки функція має похідну в точці , то функція

,

як функція , є обмеженою в . Отже, існує таке, що

, .

Тому, спрямувавши до , із рівності (4) отримуємо (2). ►

Формули (1)-(2) називаються інтегральними формулами Коші.

Зауваження 1. Інтеграл в правій частині формули (1) визначає значення функції на межі голоморфності цієї функції.

Приклад 1. За інтегральною формулою Коші

, ,

.

8. Теорема про середнє для голоморфних функцій. За означенням

,

де і .

Теорема 1. Нехай функція є голоморфною в області . Тоді для кожного і кожного виконується

, (1)

, , . (2)

Доведення. Справді, функція є голоморфною в . Тому

,

звідки випливає (1). Із (1) отримуємо, що

,

тобто (2) має місце. ►

Приклад 1. За формулою (1) .

9. Інтеграл типу Коші. Існування похідної будь-якого порядку голоморфної функції. Інтегралом типу Коші функції по шляху називається інтеграл

. (1)

Теорема 1. Якщо – спрямований шлях, функція є неперервною на , то функція , визначена формулою (1) є голоморфною в будь-якій області D, яка не містить , і має там похідні всіх порядків, які можна знайти за формулою

. (2)

Доведення. Інтеграл (1) рівномірно збігається на будь-якому компакті, який з не перетинається. Нехай . Тоді

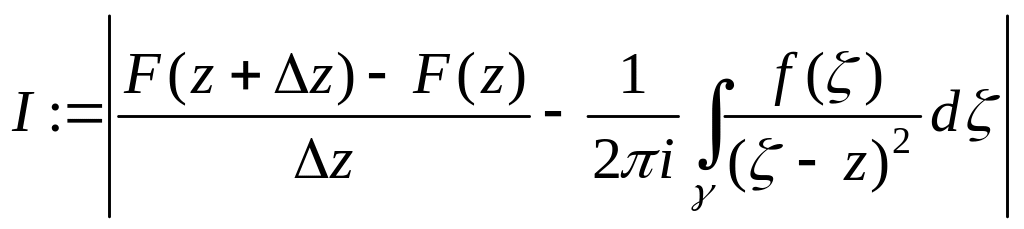
. (3)

Для кожного знайдеться таке , що для всіх , , круг буде знаходитися на додатній відстані від . Тому можна знайти таке , що якщо , то для всіх матимемо , . Тому

.

Отже, при і тому із (3) отримуємо, що має похідну в точці, яку можна знайти за формулою (2) взявши в ній . Аналогічно, розглянувши різницю

,

переконуємось, що має другу похідну, яку можна знайти за формулою (2) при і т.д. ►

Теорема 2. Нехай функція є голоморфною в області . Тоді вона має в кожній точці похідні всіх порядків, які можна знайти за формулою

, (4)

де  – довільний замкнений спрямований жордановий шлях такий, що і . Якщо крім цього, складається зі скінченного числа спрямованих замкнених жорданових кривих і функція є неперервною в , то -у похідну можна також знайти за формулою

. (5)

Доведення. Ця теорема є наслідком інтегральної формули Коші та попередньої теореми. ►

Наслідок 1. Якщо функція є голоморфною в області , то в є голоморфними також всі її похідні.

10. Теорема Морери. Таку назву має наступне твердження.

Теорема 1. Якщо функція є неперервною в області і

(1)

для будь-якого замкненого спрямованого шляху  з , то має однозначну первісну в і є голоморфною функцією в .

Доведення. З умови теореми випливає, що інтеграл

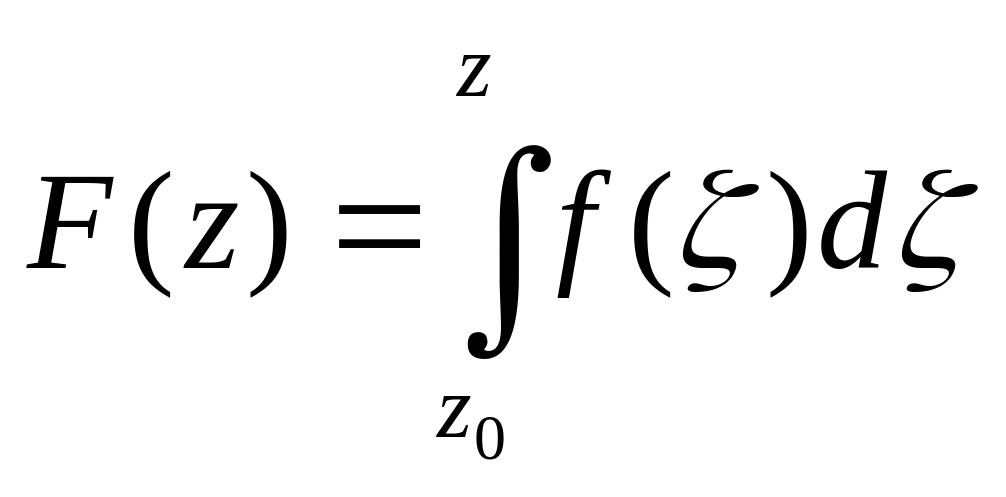, , , (2)

не залежить від шляху інтегрування в області і тому однозначна функція в області . Далі,

,

бо

.

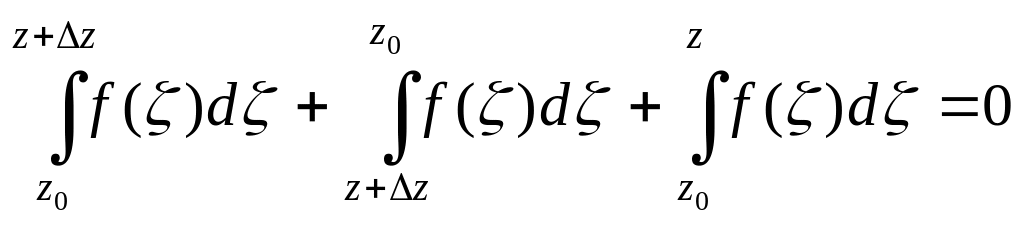Окрім цього (тут і далі інтеграл береться по відрізку),

.

Тому

. (3)

Оскільки є неперервною функцією, то

.

Тому з (3) отримуємо

, ,

звідки випливає, що має похідну в області і . Отже, є голоморфною в . Тому на підставі наслідку 1 попереднього пункту функція також є голоморфною в . ►

Наслідок 1. Якщо функція є неперервною в області і

(4)

для будь-якого трикутника такого, що , то є голоморфною в .

Теорема 2 (про усунення відрізка). Якщо функція є неперервною в області і голоморфною в , де  – відрізок з , то є голоморфною в .

Доведення. Справді, досить показати, що є голоморфною в деякій однозв’язній області такій, що . Але за узагальненою теоремою Коші для будь-якого трикутника  такого, що виконується (4). Звідси та властивостей криволінійного інтеграла випливає, що задовольняє в умови теореми Морери. Отож, є голоморфною функцією. ►