
6. Узагальнення інтегральної теореми Коші.
Теорема
1.
Нехай
межа обмеженої однозв’язної області
є замкненою жордаваною спрямованою
кривою, а функція
є голоморфною в
і неперервною в
![]() .
Тоді
.
Тоді
![]() .
(1)
.
(1)
Доведення.
Обмежимось доведенням у випадку, коли
![]() є кусково-гладкою і
є зірковою відносно деякої точки
,
тобто точку
можна з’єднати з кожною точкою
відрізком,
який лежить в
.
Можемо вважати, що
є кусково-гладкою і
є зірковою відносно деякої точки
,
тобто точку
можна з’єднати з кожною точкою
відрізком,
який лежить в
.
Можемо вважати, що
![]() .
Нехай
,
,
– параметризація
і
.
Нехай
,
,
– параметризація
і
![]() ,
,
![]() .
Шлях
лежить в
.
Отже, за теоремою Коші
.
Шлях
лежить в
.
Отже, за теоремою Коші
![]() .
(2)
.
(2)
Тому
![]()
![]() .
.
Оскільки рівномірно неперервна в , то
![]() .
.
Таким чином,
![]() ,
,
![]() ,
,
де – довжина . Звідси випливає потрібне. ►
Теорема 2. Нехай межа обмеженої області складається зі скінченного числа жорданових спрямованих кривих, а функція є голоморфною в і неперервною на . Тоді виконується (1).
Доведення.
Подамо область
у
вигляді об’єднання скінченної кількості
замкнених однозв’язних областей
![]() ,
які не мають спільних внутрішніх точок.
Застосувавши
теорему до кожної однозв’язної області
і зауваживши, що сума інтегралів по
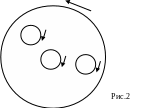
спільних частинах меж областей (див.
рис. 1) дорівнює нулеві, приходимо до
потрібного висновку. ►
,
які не мають спільних внутрішніх точок.
Застосувавши
теорему до кожної однозв’язної області
і зауваживши, що сума інтегралів по
спільних частинах меж областей (див.
рис. 1) дорівнює нулеві, приходимо до
потрібного висновку. ►

Теорема
3 (про складові контури).
Нехай
межа області
складається
із скінченного числа жорданових
спрямованих замкнених кривих і
![]() ,
,
![]() ,...,
,...,![]() – замкнені спрямовані жорданові криві,
які лежать
– замкнені спрямовані жорданові криві,
які лежать
в
,
а
![]() область з межею
область з межею
![]() .
Тоді, якщо орієнтації
,
,...,
є протилежними до їх орієнтації як
компонент
.
Тоді, якщо орієнтації
,
,...,
є протилежними до їх орієнтації як
компонент
![]() ,
а функція
голоморфна в
і неперервна в
,
а функція
голоморфна в
і неперервна в
![]() ,
то
,
то
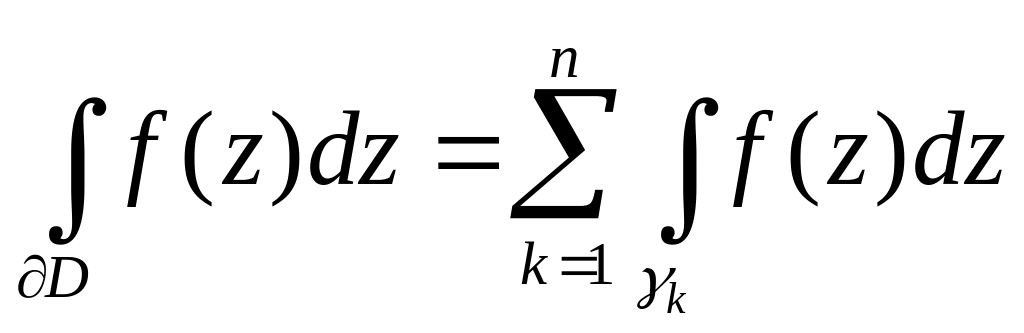 .
.
Доведення. Справді, за попередньою теоремою, застосованою до G маємо
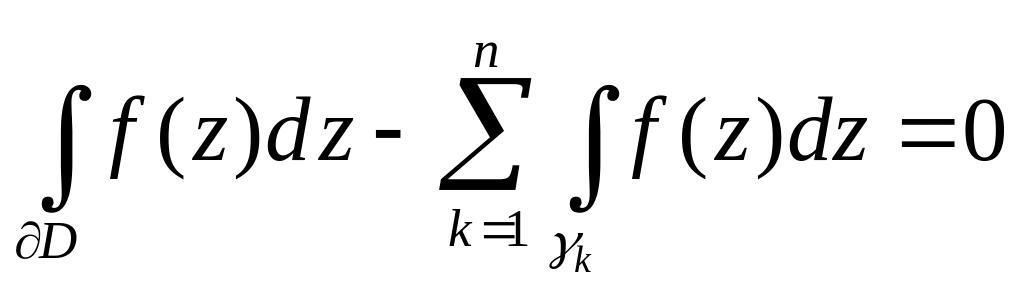 ,
,
звідки випливає потрібне. ►
Два
замкнені шляхи
![]() і
і
![]() називаються гомотопними в області
,
якщо вони є неперервними і їх можна
неперервно деформувати один в одного
не виходячи із області
.
Два незамкнені шляхи
і
називаються гомотопними в області
,
якщо їх можна неперервно деформувати
один в одного не рухаючи їх початків і
кінців та не виходячи за межі області
,
тобто якщо існує неперервна в прямокутнику
називаються гомотопними в області
,
якщо вони є неперервними і їх можна
неперервно деформувати один в одного
не виходячи із області
.
Два незамкнені шляхи
і
називаються гомотопними в області
,
якщо їх можна неперервно деформувати
один в одного не рухаючи їх початків і
кінців та не виходячи за межі області
,
тобто якщо існує неперервна в прямокутнику
![]() функція
функція
![]() така, що: а)
така, що: а)
![]() і
і
![]() при всіх
при всіх
![]() ;
б)
;
б)
![]() і
і
![]() при всіх
при всіх
![]() (у випадку замкнених шляхів умову б)
потрібно замінити умовою: б)
(у випадку замкнених шляхів умову б)
потрібно замінити умовою: б)
![]() при всіх
).
Замкнений шлях
називається гомотопним нулеві в області
,
якщо він є гомотопним кожному колу, яке
лежить в деякому крузі
при всіх
).
Замкнений шлях
називається гомотопним нулеві в області
,
якщо він є гомотопним кожному колу, яке
лежить в деякому крузі
![]() .
Якщо незамкнені шляхи
і
є гомотопними в області
,
то існує однозв’язна область
така, що
.
Якщо незамкнені шляхи
і
є гомотопними в області
,
то існує однозв’язна область
така, що
![]() .
Якщо замкнений шлях є гомотопним в
нулеві, то існує однозв’язна область
така,
що
.
Якщо замкнені шляхи
і
є гомотопними в області
,
то існує однозв’язна або двозв’язна
область
.
Якщо замкнений шлях є гомотопним в
нулеві, то існує однозв’язна область
така,
що
.
Якщо замкнені шляхи
і
є гомотопними в області
,
то існує однозв’язна або двозв’язна
область
![]() така, що
.
Якщо область
є однозв’язною, то кожні два неперервні
шляхи
і
із D,
які мають спільні початки і спільні
кінці є гомотопними в D
і кожний замкнений неперервний шлях,
який лежить в
,
є гомотопним в
нулеві. У випадку круга гомотопію шляхів
і
здійснює функція
така, що
.
Якщо область
є однозв’язною, то кожні два неперервні
шляхи
і
із D,
які мають спільні початки і спільні
кінці є гомотопними в D
і кожний замкнений неперервний шлях,
який лежить в
,
є гомотопним в
нулеві. У випадку круга гомотопію шляхів
і
здійснює функція
![]() .
Загальний випадок зводиться до круга
шляхом покриття
.
Загальний випадок зводиться до круга
шляхом покриття![]() скінченною кількістю кругів. Враховуючи
сказане вище, із теореми Коші отримуємо
наступне твердження.
скінченною кількістю кругів. Враховуючи
сказане вище, із теореми Коші отримуємо
наступне твердження.
Теорема 4. Інтеграли голоморфної в області функції по спрямованим і гомотопним в шляхам є рівними. Інтеграл голоморфної в області функції по спрямованому і гомотопному в шляху дорівнює нулеві.
Зауваження
1.
В
двозв’язній області
![]() кожний замкнений неперервний шлях є
гомотопним нулеві або деякому колу
кожний замкнений неперервний шлях є
гомотопним нулеві або деякому колу
![]() ,
,
![]() ,
де
,
де
![]() ,
,
![]() ,
,
![]() ,
яке обходиться
,
яке обходиться
![]() раз в додатному напрямку, якщо
раз в додатному напрямку, якщо
![]() і у від’ємному, якщо
і у від’ємному, якщо
![]() .
Кожний незамкнений шлях в
з початком в точці
.
Кожний незамкнений шлях в
з початком в точці
![]() і кінцем в точці
і кінцем в точці
![]() є гомотопним об’єднанню деякого кола
є гомотопним об’єднанню деякого кола
![]() і деякого неперервного шляху з початком
в точці
і деякого неперервного шляху з початком
в точці
![]() )
і кінцем в точці
,
який лежить в деякій однозв’язній
області, яка не містить точки
)
і кінцем в точці
,
який лежить в деякій однозв’язній
області, яка не містить точки
![]() .
.
Приклад
1.
![]() .
Справді, функція
.
Справді, функція
![]() є голоморфною в області
є голоморфною в області
![]() і неперервною в її замиканні. Тому за
теоремою 1
і неперервною в її замиканні. Тому за
теоремою 1
![]() .
.
Але
![]() .
.
Звідси отримуємо потрібний висновок.
