
Інтегральні теореми Коші
Розділ 3. Інтегральні теореми Коші
1.
Інтеграл Рімана. Нехай
задано функцію
![]() .
Розглянемо таке розбиття
.
Розглянемо таке розбиття
![]() проміжка
проміжка
![]() ,
що
,
що
![]() .
На кожному проміжку
.
На кожному проміжку
![]() візьмемо довільну точку
візьмемо довільну точку
![]() і складемо суму
і складемо суму
![]() ,
(1)
,
(1)
де
![]() .
Інтегралом Рімана функції
по проміжку
називається границя
.
Інтегралом Рімана функції
по проміжку
називається границя
![]() ,
,
![]() ,
(2)
,
(2)
яка позначається символом
![]() .
.
Іншими словами,
![]() , (3)
, (3)
де
![]() ,
,
![]() .
Інтеграл Рімана функції
має звичайні для інтегралів властивості.
Зокрема, для нього справедлива формула
Лейбніца-Ньютона. Проте, при знаходженні
первісної слід бути обережним, оскільки
вона може виражатись через багатозначні
функції. В такому випадку інколи
доцільніше скористатись формулою (3) і
звести знаходження розглядуваного
інтеграла до знаходження двох інтегралів
Рімана дійснозначних функцій.
.
Інтеграл Рімана функції
має звичайні для інтегралів властивості.
Зокрема, для нього справедлива формула
Лейбніца-Ньютона. Проте, при знаходженні
первісної слід бути обережним, оскільки
вона може виражатись через багатозначні
функції. В такому випадку інколи
доцільніше скористатись формулою (3) і
звести знаходження розглядуваного
інтеграла до знаходження двох інтегралів
Рімана дійснозначних функцій.
2.
Криволінійний інтеграл першого роду
функції
![]() .
Нехай
задано функцію
і шлях
.
Нехай
задано функцію
і шлях
![]() .
Розглянемо таке розбиття
проміжку
,
що
.
На кожному проміжку
візьмемо довільну точку
і складемо суму
.
Розглянемо таке розбиття
проміжку
,
що
.
На кожному проміжку
візьмемо довільну точку
і складемо суму
![]() ,
(1)
,
(1)
де
![]() ,
,
![]() ,
,
![]() .
Криволінійним інтегралом першого роду
функції
.
Криволінійним інтегралом першого роду
функції
![]() по шляху
по шляху
![]() називається границя
називається границя
, , (2)
де
![]() ,
яка позначається одним із символів
,
яка позначається одним із символів
![]() ,
,
![]() .
.
Якщо
границя (2) існує і є скінченною, то
називається інтегрованою на шляху
![]() .
Криволінійний інтеграл першого роду
має звичайні для інтегралів властивості,
серед яких виділимо такі.
.
Криволінійний інтеграл першого роду
має звичайні для інтегралів властивості,
серед яких виділимо такі.
Теорема
1. Для
будь-якого спрямованого шляху
з
довжиною
![]() виконується
виконується
![]() ,
,
Теорема 2. Кожна неперервна на спрямованому шляху функція є інтегрованою і
![]() .
.
Теорема 3. Для будь-якої інтегрованої на спрямованому шляху функції виконується
![]() .
.
Теорема 4. Якщо неперервна на гладкому шляху , то
![]() .
.
Ці
властивості випливають безпосередньо
з означення та властивостей криволінійних
інтегралів функції з
![]() в
в
![]() .
Правда, потрібно врахувати, що
.
Правда, потрібно врахувати, що
![]() ,
де
,
де
![]() ,
а
,
а
![]() .
.
Доведемо, наприклад, теорему 4. Нехай , , , а . Тоді
![]()
![]()
![]() ,
,
що і потрібно було довести. ►
Приклад
1.
Знайдемо![]() ,
де
,
де
![]() ,
,
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
![]() .
.
3. Інтеграл функції по шляху (криволінійний інтеграл другого роду). Нехай задано функцію і шлях . Розглянемо таке розбиття проміжку , що . На кожному проміжку візьмемо довільну точку і складемо суму
![]() ,
,
де
,
,
![]() .
Інтегралом функції
по шляху
або криволінійним інтегралом другого
роду функції
по шляху
називається границя
.
Інтегралом функції
по шляху
або криволінійним інтегралом другого
роду функції
по шляху
називається границя
![]() ,
,
(1)
,
,
(1)
де
.
Отож, криволінійний інтеграл другого
роду функції
по шляху
![]() – це інтеграл Стілтьєса
– це інтеграл Стілтьєса
![]()
функції
![]() по проміжку
.
Його позначають також символами
по проміжку
.
Його позначають також символами
![]() ,
,
![]() .
.
Якщо границя (1) існує і є скінченною, то функція називається інтегрованою на . Криволінійний інтеграл другого роду має звичайні для інтегралів властивості, серед яких виділимо такі.
Теорема
1.
![]() ,
де
,
де
![]() – початок шляху, а
– початок шляху, а
![]() – кінець.
– кінець.
Теорема
2.
![]() ,
якщо
останній інтеграл існує, де
,
якщо
останній інтеграл існує, де
![]() – шлях, протилежний до шляху
.
– шлях, протилежний до шляху
.
Теорема 3.
![]() ,
,
якщо останні інтеграли існують, де , .
Теорема 4. Якщо функція є неперервною на спрямованому шляху , то вона інтегрована і
![]() .
.
Теорема
5. Якщо
функція
є неперервною на гладкому шляху
![]() ,
то
,
то
![]() .
(2)
.
(2)
Теореми 1-5 випливають безпосередньо з означень і властивостей криволінійного інтеграла в . Рівність (2) інколи беруть за означення інтеграла по . Теорема 5 показує, що інтеграли виду (1) по еквівалентним гладким шляхам є рівними.
Звичайною
первісною функції
або функції
на гладкому шляху
називається така функція
![]() ,
що
,
що
![]() ,
тобто така функція
,
що
,
тобто така функція
,
що
![]() .
.
Теорема
6. Якщо
![]() – звичайна первісна функції
на гладкому шляху
і функція
– звичайна первісна функції
на гладкому шляху
і функція
![]() неперервна на
,
то
неперервна на
,
то
![]() .
.
Доведення. Це твердження випливає із теореми 5. ►
Теорема
7. Якщо
![]() – гладкий шлях, функція
– гладкий шлях, функція
![]() є неперервною в області
є неперервною в області
![]() і має в
однозначну первісну, тобто існує така
функція
і має в
однозначну первісну, тобто існує така
функція
![]() ,
що для всіх
,
що для всіх
![]() виконується
виконується
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() .
.
Доведення.
Функція
![]() є звичайною первісною функції
на
.
Тому це твердження випливає з теореми
6. ►
є звичайною первісною функції
на
.
Тому це твердження випливає з теореми
6. ►
Наведену нижче теорему 8 називають також лемою Гурса.
Теорема
8. Якщо
функція
є неперервною в області
і
– спрямований шлях, який лежить в
,
то для кожного
![]() знайдеться ламана
знайдеться ламана
![]() (тобто шлях, який складається із
скінченного числа відрізків), яка лежить
в
і
(тобто шлях, який складається із
скінченного числа відрізків), яка лежить
в
і
![]() .
.
причому – замкнена ламана, якщо – замкнений шлях.
Доведення.
Оскільки
![]() – компакт, то існує така область
– компакт, то існує така область
![]() ,
що
,
що
![]() і відстань
і відстань
![]() між
і
між
і
![]() є додатною. З рівномірної неперервності
в
випливає, що
є додатною. З рівномірної неперервності
в
випливає, що
![]() .
.
Оскільки
шлях
–
спрямований, то можна знайти такий
діаметр
![]() розбиття
розбиття
![]() проміжку
,
що
довжина звуження
на кожний проміжок
(це звуження позначаємо
проміжку
,
що
довжина звуження
на кожний проміжок
(це звуження позначаємо
![]() )
буде меншою за
)
буде меншою за
![]() .
Тоді відрізок
.
Тоді відрізок
![]() і утворена цими відрізками ламана також
належить
.
Тому враховуючи, що
і утворена цими відрізками ламана також
належить
.
Тому враховуючи, що
![]() ,
,
маємо
![]()
![]() .
.
Отож,
![]() ,
,
де
![]() – довжина
.
Звідси випливає потрібне. ►
– довжина
.
Звідси випливає потрібне. ►
Теорема
9. Якщо
функція
є неперервною в області
і для будь-якого трикутника
такого, що
![]() ,
виконується
,
виконується
![]() ,
,
то для кожного замкненого жорданового спрямованого контуру , що лежить в , виконується
![]() .
.
Д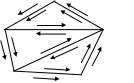 оведення.
Справді, інтеграл по
можна як завгодно наблизити
оведення.
Справді, інтеграл по
можна як завгодно наблизити
Рис. 1
інтегралами по замкненій ламаній . З іншого боку, інтеграл по замкненій ламаній можна подати (див. рис. 1) у вигляді суми інтегралів по межі трикутників. ►
Приклад 1. Знайдемо
![]() ,
,
де
,
.
Маємо
![]() .
Тому
.
Тому
![]() .
.
Приклад
2.
Покажемо,
що для будь-яких
![]() і
і
![]() виконується
виконується
![]()
Справді,
![]()
Приклад
3.
Нехай
–
шлях, який є частиною кола:
![]() ,
,
![]() .
Тоді
.
Тоді
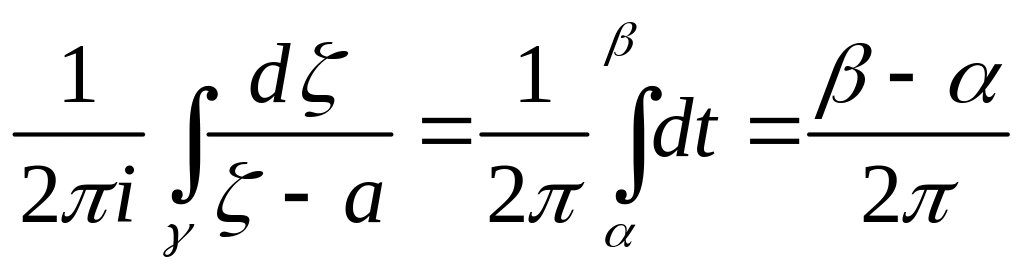
і,
зокрема, якщо
– півколо, тобто
![]() ,
то
,
то
![]() .
.
Зауваження
1.
У
випадку, коли
є відрізком
![]() з початком в точці
з початком в точці
![]() і кінцем в точці
і кінцем в точці
![]() ,
тобто
,
тобто
![]() ,
означення криволінійного інтеграла
другого роду
,
означення криволінійного інтеграла
другого роду
![]() збігається з означенням інтеграла
Рімана
.
У випадку, коли криволінійний інтеграл
другого роду не залежить від шляху
інтегрування в деякій області, його
позначають символом
збігається з означенням інтеграла
Рімана
.
У випадку, коли криволінійний інтеграл
другого роду не залежить від шляху
інтегрування в деякій області, його
позначають символом
![]() .
.
4.
Функція на шляху.
Функцією на шляху
називається будь-яка однозначна функція
![]() .
Можна дати трохи інше, але еквівалентне
означення функції на шляху, яким ми
частіше будемо користуватись. Однозначною
гілкою багатозначної функції
на
шляху
називається така однозначна функція
,
що для всіх
виконується
.
Можна дати трохи інше, але еквівалентне
означення функції на шляху, яким ми
частіше будемо користуватись. Однозначною
гілкою багатозначної функції
на
шляху
називається така однозначна функція
,
що для всіх
виконується
![]() .
Цю однозначну гілку позначають через
.
Цю однозначну гілку позначають через
![]() або
,
а також через
,
хоч ці позначення є природними тільки
у випадку жордановості .
Кожна функція
є однозначною гілкою деякої функції
або
,
а також через
,
хоч ці позначення є природними тільки
у випадку жордановості .
Кожна функція
є однозначною гілкою деякої функції
![]() ,
тобто є функцією на шляху
.
Справді, позначимо через
таку функцію із
в
,
тобто є функцією на шляху
.
Справді, позначимо через
таку функцію із
в
![]() ,
для якої образом кожного
,
для якої образом кожного
![]() є
ті
є
ті
![]() ,
для яких існує
таке, що
,
для яких існує
таке, що
![]() і
і
![]() .
Тому
означення функції на шляху можна
сформулювати іншим чином.
Функцією
на шляху
називається будь-яка функція
,
яка є однозначною гілкою на
деякої багатозначної функції
.
.
Тому
означення функції на шляху можна
сформулювати іншим чином.
Функцією
на шляху
називається будь-яка функція
,
яка є однозначною гілкою на
деякої багатозначної функції
.
Інтегралом функції по шляху називається інтеграл Стілтьєса
.
Якщо
![]() є однозначною гілкою на
деякої багатозначної функції
є однозначною гілкою на
деякої багатозначної функції
![]() ,
то цей інтеграл позначають також
символами
,
то цей інтеграл позначають також
символами
, .
Якщо – однозначна функція, то функція є функцією на шляху і останнє означення інтеграла функції збігається з означенням криволінійного інтеграла другого роду функції по .
Криволінійним інтегралом першого роду по шляху називається границя
![]() .
.
Якщо – однозначна функція, то функція є функцією на шляху і останнє означення інтеграла функції збігається з означенням криволінійного інтеграла першого роду функції по . Якщо є однозначною гілкою на деякої багатозначної функції , то цей інтеграл позначають також символами
![]() ,
,
![]() .
.
Зустрічаються також невластиві криволінійні інтеграли та інтеграли в розумінні головного значення. Їхні означення наведемо пізніше.
Приклад
1.
Функція
![]() ,
,
![]() ,
є однозначною гілкою функції
,
є однозначною гілкою функції
![]() на шляху
на шляху
![]() ,
,
а функція
,
,
а функція
![]() ,
,
![]() ,
є однозначною гілкою функції
,
є однозначною гілкою функції
![]() на шляху
на шляху
![]() ,
.
,
.
5. Інтегральна теорема Коші. Таку назву має наступне твердження.
Теорема 1. Якщо функція є голоморфною в однозв’язній області , то для кожного замкненого спрямованого шляху , що лежить в , виконується
. (1)
Доведення.
Ми доведемо спочатку цю теорему при
додатковій умові: функція
![]() є неперервною в
.
Тоді функції
і
мають неперервні частинні похідні в
і з умов Коші-Рімана отримуємо
є неперервною в
.
Тоді функції
і
мають неперервні частинні похідні в
і з умов Коші-Рімана отримуємо
![]() ,
,
![]() .
.
Тому, враховуючи, що
![]() ,
,
та умови рівності нулеві інтеграла по замкненому шляху для криволінійних інтегралів в , отримуємо (1). Переходимо до доведення теореми Коші в загальному випадку. Досить показати, що
, (2)
де
![]() – довільний трикутник такий, що
– довільний трикутник такий, що![]() .
Припустимо протилежне, тобто що існує
трикутник
такий, що
.
Припустимо протилежне, тобто що існує
трикутник
такий, що
![]() .
.
За
допомогою середніх ліній розіб’ємо
на чотири трикутники. Оскільки інтеграл
по сумі інтегралів
![]() дорівнює по межі чотирьох
дорівнює по межі чотирьох
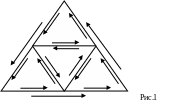
отриманих
трикутників, то знайдеться один із них
(позначимо його через
![]() )
такий, що
)
такий, що
![]() .
.
Тепер
трикутник
ділимо за допомогою середніх ліній на
чотири трикутники і т.д. В результаті
отримаємо послідовність
![]() трикутників таку, що
трикутників таку, що
![]() .
(3)
.
(3)
Проекціями![]() на дійсну пряму будуть замкнені вкладені
відрізки, які за принципом вкладених
проміжків мають спільну точку. Звідси
випливає, що всі замкнені трикутники
мають спільну точку
на дійсну пряму будуть замкнені вкладені
відрізки, які за принципом вкладених
проміжків мають спільну точку. Звідси
випливає, що всі замкнені трикутники
мають спільну точку
![]() .
Функція
має похідну в точці
.
Тому
.
Функція
має похідну в точці
.
Тому
![]()
![]() ,
де
,
де
![]() коли
коли
![]() .
Тому
.
Тому
![]()
![]() ,
,
бо,
як вже доведено вище, для функцій, які
мають неперервну похідну, твердження
теореми є справедливим. Далі, для кожного
![]() існує
існує
![]() таке, що
таке, що
![]() ,
якщо
,
якщо
![]() .
Всі трикутники
з
номерами
.
Всі трикутники
з
номерами
![]() лежать
в крузі
лежать
в крузі
![]() .
Тому для кожного
.
Тому для кожного
![]() ,
,
,
,
де
![]() –
периметр
–
периметр
![]() .
Але
.
Але![]() ,
де
,
де
![]() –
периметр
.
Отже,
–
периметр
.
Отже,
![]() ,
,
,
,
а це суперечить (3). Таким чином, (2) виконується і теорема доведена. ►
Приклад
1.
Функція
![]() є голоморфною в двозв’язній області
є голоморфною в двозв’язній області
![]() ,
а
,
а
![]() .
.
Отже, вимога однозв’язності області в теоремі 1 є істотною.
