
- •Розділ 1. Множини комплексних чисел та функції
- •Оскільки
- •Приклад 4. Знайдемо . Оскільки і , то , , .
- •8. Степінь з довільним показником. За означенням
- •Гіперболічним косинусом комплексного числа називається комплексне число
- •23. Запитання для самоконтролю.
- •24. Вправи і задачі.
- •1.24. З’ясуйте можливість визначення значення функції в точці так, щоб продовжена функція була неперервною в цій точці:
23. Запитання для самоконтролю.
1. Що називаємо модулем та аргументом комплексного числа?
2. Який зміст можуть мати символи ,, ” та ,, ”?
3.
Як слід розуміти символ ,,![]() ”?
”?
4. Запишіть формулу Муавра.
5. Сформулюйте означення кореня n-го степеня з компексного числа і доведіть формулу для його знаходження.
6.
Який зміст мають символи ,,![]() ”
та ,,
”
та ,,![]() ”?
”?
7.
Сформулюйте означення
![]() та доведіть, що
та доведіть, що
![]() .
.
8. Сформулюйте означення логарифма комплексного числа і виведіть формулу для знаходження логарифмів.
9.
Який зміст можуть мати символи ,,
”
та ,,![]() ”?
”?
10.
Як Ви розумієте символ ,,![]() ”?
”?
11.
Сформулюйте означення
![]() .
.
12. Який зміст можуть мати символи ,, ” та ,, ”?
13. Скільки різних значень може приймати ? Для яких та ця кількість є скінченною?
14. Що називаємо синусом комплексного числа?
15.
Доведіть, що
![]() .
.
16.
Доведіть, що
![]() .
.
17. Чи існують такі , для яких нерівність не виконується.
24. Вправи і задачі.
1.1. Знайдіть модуль і головне значення аргументу комплексного числа :
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() .
.
9.
![]() . 10.
. 10.
![]() .
.
11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() .
.
15.
![]() . 16.
. 16.
![]() .
.
17.
![]() . 18.
. 18.
![]() .
.
19.
![]() . 20.
. 20.
![]() .
.
21.
![]() . 22.
. 22.
![]() .
.
23.
![]() . 24.
. 24.
![]() .
.
25.
![]() . 26.
.
. 26.
.
27.
![]() . 28.
. 28.
![]() .
.
29.
![]() . 30.
. 30.
![]() .
.
31.
![]() .
32.
.
32.
![]() .
.
33.
![]() .
34.
.
34.
![]() .
.
35.
![]() .
36.
.
36.
![]() .
.
37.
![]() .
38.
.
38.![]() .
.
39.
![]() 40.
40.
![]()
41.
![]() .
42.
.
42.
![]() .
.
43.
![]() .
44.
.
44.
![]() .
.
45.
![]() .
46.
.
46.
![]() .
.
47.
![]() . 48.
. 48.
![]() .
.
49.
![]() . 50.
. 50.
![]() .
.
1.2. Доведіть:
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() .
.
9.
![]() . 10.
. 10.
![]() .
.
11.
![]() .
.
1.3. Запишіть комплексне число в показниковій і тригонометричній формах:
1.
![]() . 2.
. 2.
![]() . 3.
. 3.
![]() .
.
4.
![]() . 5.
. 5.
![]() . 6.
. 6.
![]() .
.
7.
![]() .
8.
.
8.
![]() . 9.
. 9.
![]() .
.
10.
![]() ,
,
![]() . 11.
. 11.
![]() .
.
1.4. Запишіть комплексне число в алгебраїчній формі:
1.
![]() . 2.
. 2.
![]() . 3.
. 3.
![]() .
.
4.
![]() . 5.
. 5.
![]() . 6.
. 6.
![]() .
.
1.5. Знайдіть:
1.
![]() . 2.
. 2.
![]() . 3.
. 3.
![]() .
.
4.
![]() . 5.
. 5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() . 9.
. 9.
![]() .
.
10.
 . 11.
. 11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() . 15.
. 15.
![]() .
.
16.
![]() . 17.
. 17.
![]() . 18.
. 18.
![]() .
.
19.
![]() . 20.
. 20.
![]() . 21.
. 21.
![]() .
.
1.6. Знайдіть:
1.
![]() . 2.
. 2.
![]() . 3.
. 3.
![]() .
.
4.
![]() . 5.
. 5.
![]() . 6.
. 6.
![]() .
.
7.
![]() .
8.
.
8.
![]() . 9.
. 9.
![]() .
.
10.
![]() . 11.
. 11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() . 15.
. 15.
![]() .
.
16.
![]() . 17.
. 17.
![]() . 18.
. 18.
![]() .
.
1.7.
Які знаки можна поставити між множинами
,
та
![]() ?
?
1.
![]() ,
,
![]() ,
,
![]() .
.
2.
![]() ,
,
![]() ,
,
![]() .
.
1.8.
Знайдіть
![]() ,
,
AB
і з’ясуйте, чи
,
,
AB
і з’ясуйте, чи
![]() :
:
1.
,
![]() .
2.
,
.
2.
,
![]() .
.
3.
![]() .
4.
.
4.
![]() . 5.
. 5.
![]() .
.
1.9.
Виходячи
з означення
![]() i
,
доведіть формули:
i
,
доведіть формули:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
1.10. Розв’яжіть рівняння:
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
.
. 6.
.
7.
![]() . 8.
. 8.
![]() .
.
9.
![]() . 10.
. 10.
![]() .
.
11.
![]() .
12.
.
12.
![]() .
.
13.
![]() . 14.
. 14.
![]() .
.
15.
![]() . 16.
. 16.
![]() .
.
17.
![]() . 18.
. 18.
![]() .
.
19.
![]() . 20.
. 20.
![]() .
.
21.
![]() . 22.
. 22.
![]() .
.
1.11. Доведіть, що для всіх виконується
![]() .
.
1.121. Доведіть, що для всіх виконується
![]() .
.
1.13.
Доведіть, що для всіх
![]() виконується:
виконується:
1.
 .
.
2.
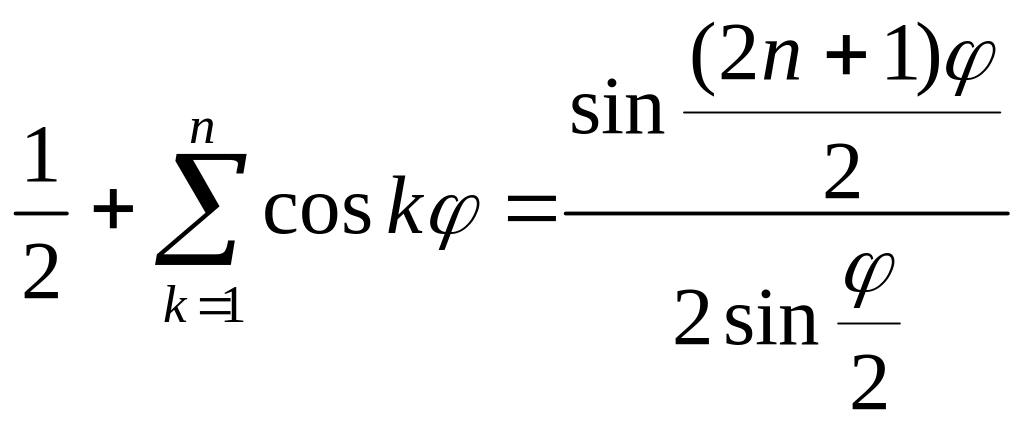 .
.
1.14.
Нехай
![]() ,
,![]() ,...,
,...,![]() – різні значення
– різні значення
![]() .
Доведіть, що
.
Доведіть, що
![]() .
.
1.15. Знайдіть границі:
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
.
7.
 .
8.
.
8.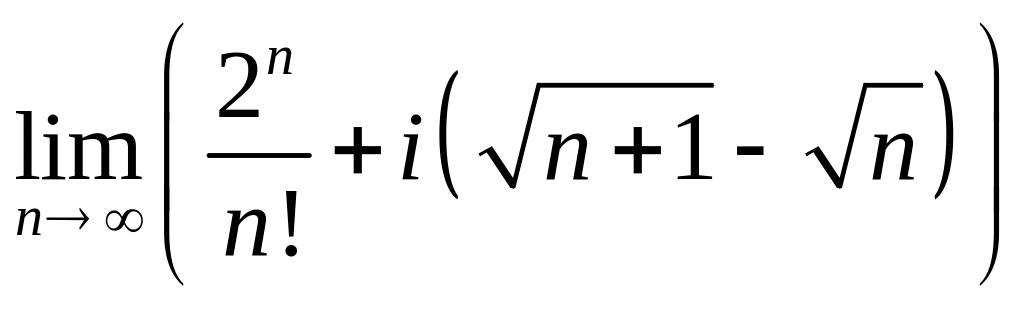 .
.
9.
![]() .
10.
.
10.
![]() .
.
1.16. Для яких збіжними в є послідовності?
1.
![]() .
2.
.
2.
![]() . 3.
. 3.
![]() .
.
1.17. Знайдіть часткові границі послідовностей:
1.
![]() . 2.
. 2.
![]() .
.
1.18. Наведіть приклад послідовності точок із правої півплощини граничними точками якої є всі точки уявної осі.
1.19. Дослідіть на збіжність ряди:
1.
![]() . 2.
. 2.
![]() .
3.
.
3.
![]() .
.
4.
![]() .
5.
.
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() . 8.
. 8.
![]() .
9.
.
9.
![]() .
.
10.
![]() . 11.
. 11.
 .
12.
.
12.
![]() .
.
13.
![]() . 14.
. 14.
![]() .
15.
.
15.
![]() .
.
16.
 . 17.
. 17.
![]() .
18.
.
18.
![]() .
.
1.20.
Напишіть
рівняння дотичної до шляху
точці
![]() ,
де
– середина вказаного проміжку і
,
де
– середина вказаного проміжку і
![]() .
Які з цих шляхів є гладкими, кусково-гладкими,
жордановими, еквівалентними, замкненими?
.
Які з цих шляхів є гладкими, кусково-гладкими,
жордановими, еквівалентними, замкненими?
1.
![]() ,
,
![]() . 2.
. 2.
![]() ,
.
,
.
3.
,
![]() . 4.
. 4.
![]() ,
.
,
.
5.
,
![]() . 6.
. 6.
![]() ,
.
,
.
7.
![]() ,
. 8.
,
. 8.
![]() ,
,
![]() .
.
9.
![]() ,
. 10.
,
. 10.
![]() ,
,
![]() .
.
11.
![]() ,
,
![]() .
.
1.21. Зобразіть множини. Які з цих множин є областями (однозв’язними, двозв’язними і т.д.)?
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() . 8.
. 8.
![]() .
.
9.
![]() .
10.
.
10.
![]() .
.
11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() .
.
15.
![]() . 16.
. 16.
![]() .
.
17.
.
18.
![]() .
.
19.
![]() . 20.
. 20.
![]() .
.
21.
![]() . 22.
. 22.
![]() .
23.
.
23.
![]() .
24.
.
24.
![]() .
25.
.
25.
![]() .
26.
.
26.
![]() .
27.
.
27.
![]() . 28.
. 28.
![]() .
29.
.
29.
![]() . 30.
. 30.
![]() .
31.
.
32.
.
31.
.
32.
![]() .
33.
. 34.
.
33.
. 34.
![]() .
35.
.
35.
![]() . 36.
. 36.
![]() .
.
37.
![]() . 38.
. 38.
![]() .
.
39.
![]() .
.
40.
![]()
 .
.
1.22. Знайдіть шлях, який є параметризацією межі області :
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() .
.
1.23. Доведіть формули (тут ):
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() ,
якщо
.
,
якщо
.
12.
![]() ,
якщо
.
,
якщо
.
13.
![]() ,
,
![]() .
.
14.
![]() ,
,
![]() .
.
15.
![]() ,
.
,
.
16.
![]() ,
.
,
.
