
- •Розділ 5. Лишки та їх застосування до знаходження інтегралів
- •2. Основна теорема про лишки.
- •Приклад 1. Згідно зі сказаним вище, якщо , то
- •4. Знаходження деяких невласних інтегралів.
- •5. Лема Жордана.
- •7.1. Знаходження інтегралів .
- •7.2. Знаходженя інтегралів .
- •7.3. Знаходженя інтегралів .
- •9. Запитання для самоконтролю.
- •10. Вправи і задачі до п’ятого розділу.
9. Запитання для самоконтролю.
1. Що називаємо залишком функції в точці ?
2. Що називаємо залишком функції в ?
3. Як знаходяться залишок функції через лоранівські коефіцієнти?
4. Як знаходяться залишок функції в простому полюсі?
5. Як знаходяться залишок функції в полюсі заданної кратності?
6. Сформулюйте і доведіть основну теорему про залишки.
7. Сформулюйте і доведіть лему Жордана.
8. Обґрунтуйте відомі вам методи обчислення інтегралів тригономе-тричних функцій за допомогою залишків.
9. Обґрунтуйте відомі вам методи обчислення невласних інтегралів за допомогою залишків.
10.Що називаємо перетворенням Лапласа?
11.Сформулюйте і обґрунтуйте відомі вам властивості перетворення Лапласа.
10. Вправи і задачі до п’ятого розділу.
5.1. Обчисліть
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
.
4.
![]() .
5.
.
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() .
8.
.
8.
![]() .
9.
.
9.
![]() .
.
10.
![]() .
11.
.
11.
![]() .
12.
.
12.
![]() .
.
13.
![]() .
14.
.
14.
![]() .
15.
.
15.
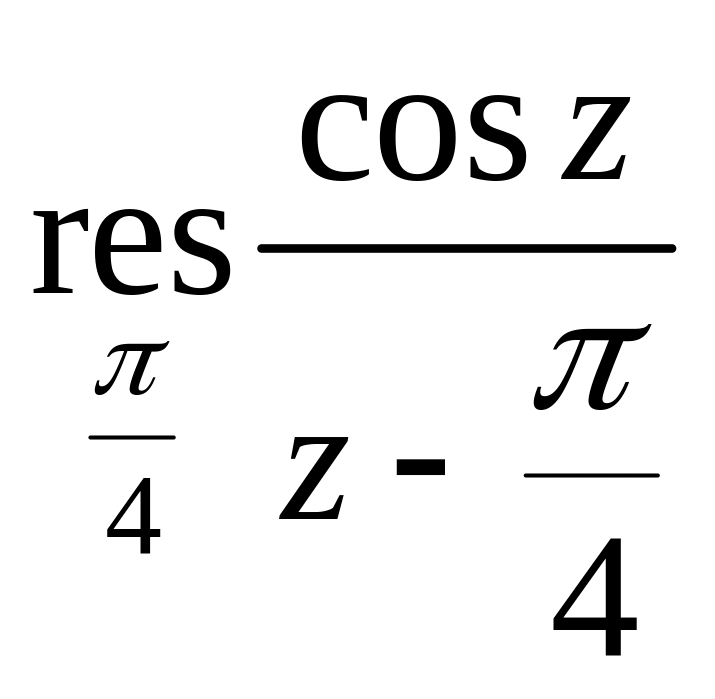 .
.
16.
![]() .
17.
.
17.
![]() .
18.
.
18.
![]() .
.
5.2. Доведіть твердження:
1. Якщо є усувною ізольованою особливою точкою функції f, то
![]() .
.
2.
Якщо
![]() ,
де функція
є голоморфною
в точці z0.
Тоді
,
де функція
є голоморфною
в точці z0.
Тоді
![]() .
.
3. Якщо функція f в точці z0 має нуль п-го порядку, а функція є голоморфною в цій точці, то
![]() .
.
4.
Якщо функція
f має
вигляд
![]() ,
де функція
,
де функція
![]() є голоморфною в точці
є голоморфною в точці
![]() ,
то
,
то
![]() .
.
5. Для кожної парної функції f виконується
![]() ,
,
якщо написані лишки мають зміст.
6. Для парної функції f має місце
![]() ,
,
якщо написані лишки мають зміст.
5.3. Знайдіть лишки функції f в усіх скінченних особливих точках
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
.
4.
![]() .
5.
.
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() .
8.
.
8.
![]() .
9.
.
9.
![]() .
.
10.
![]() .
11.
.
11.
![]() .
12.
.
12.
![]() .
.
5.4. Знайдіть лишки функції f в
1.
![]() .
2.
.
3.
.
2.
.
3.
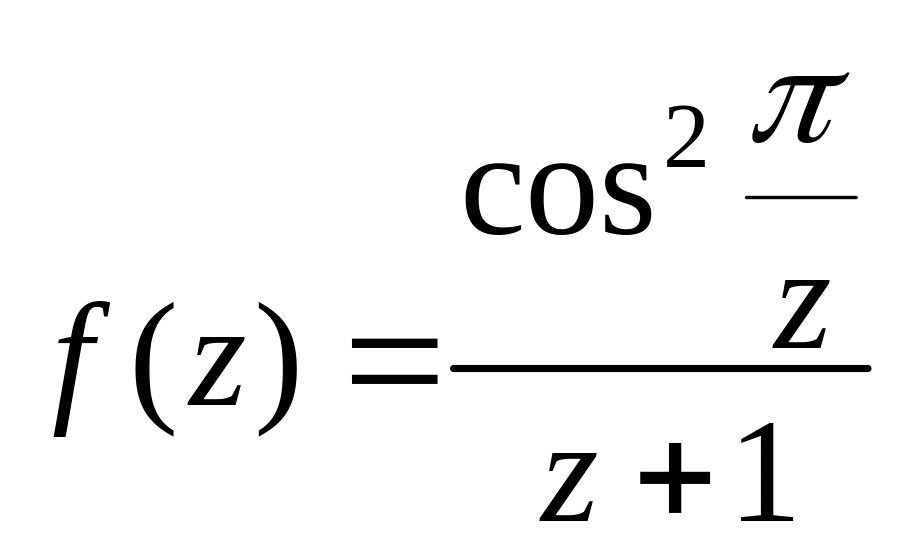 .
.
4.
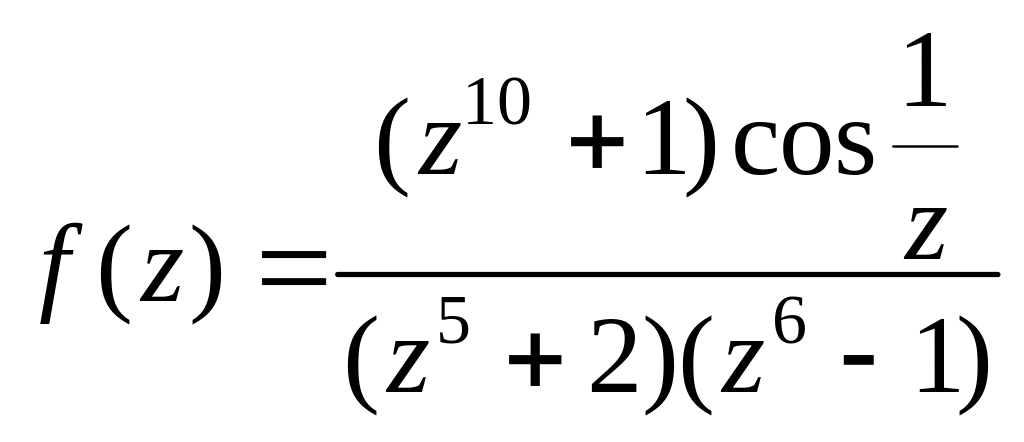 .
5.
.
5.
![]()
5.5. Знайдіть лишки в усіх ізольованих особливих точках функції f
1.
![]() .
2.
.
2.
![]()
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() .
8.
.
8.
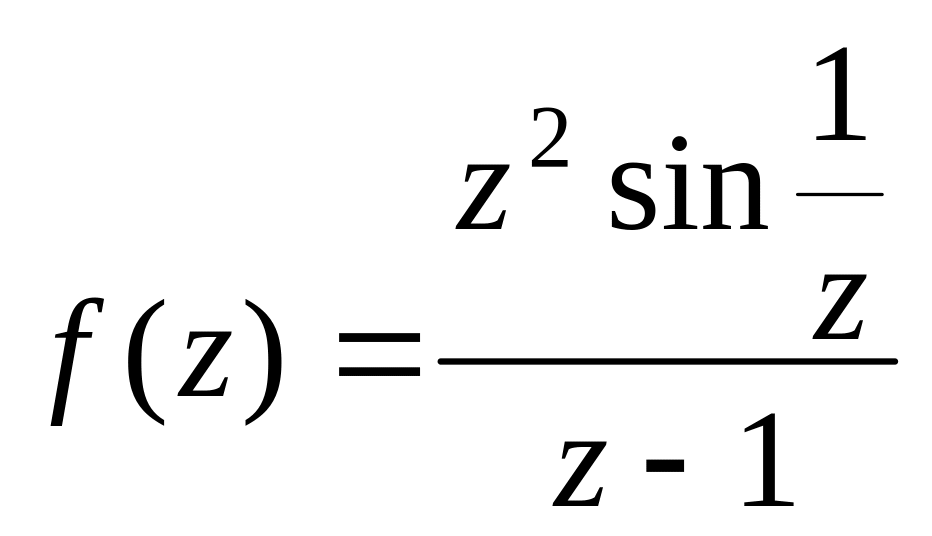 .
.
9.
![]() .
10.
.
10.
![]() .
.
11.
![]() .
12.
.
12.
![]() .
.
13.
![]() .
14.
.
14.
![]() .
.
15.
![]() .
16.
.
16.
![]() .
.
17.
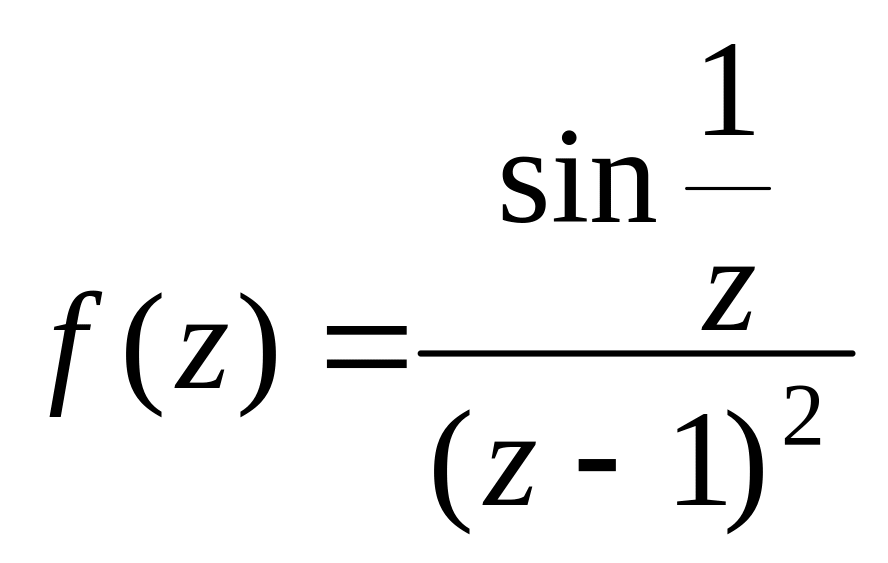 .
18.
.
18.
![]() .
.
19.
![]() .
20.
.
.
20.
.
21.
.
22.
![]() .
.
23.
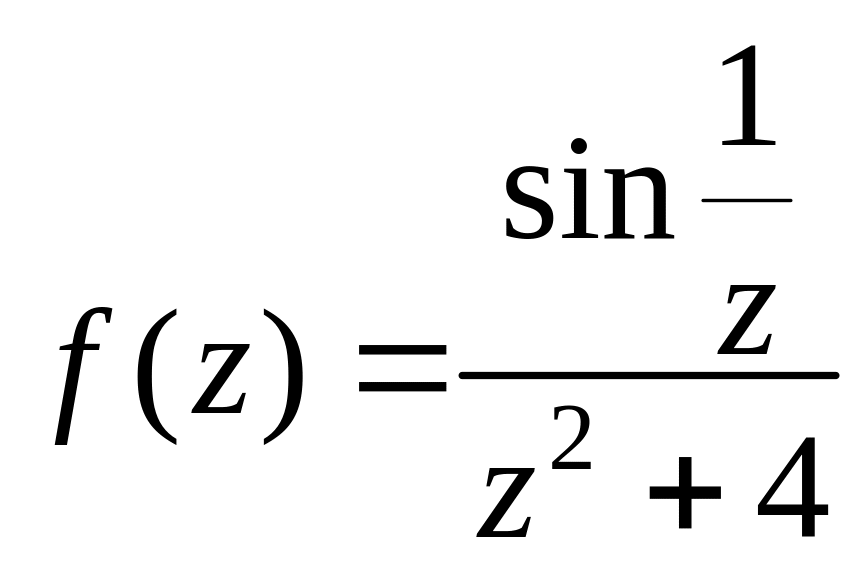 .
24.
.
24.
![]() .
.
25.
![]() .
26.
.
26.
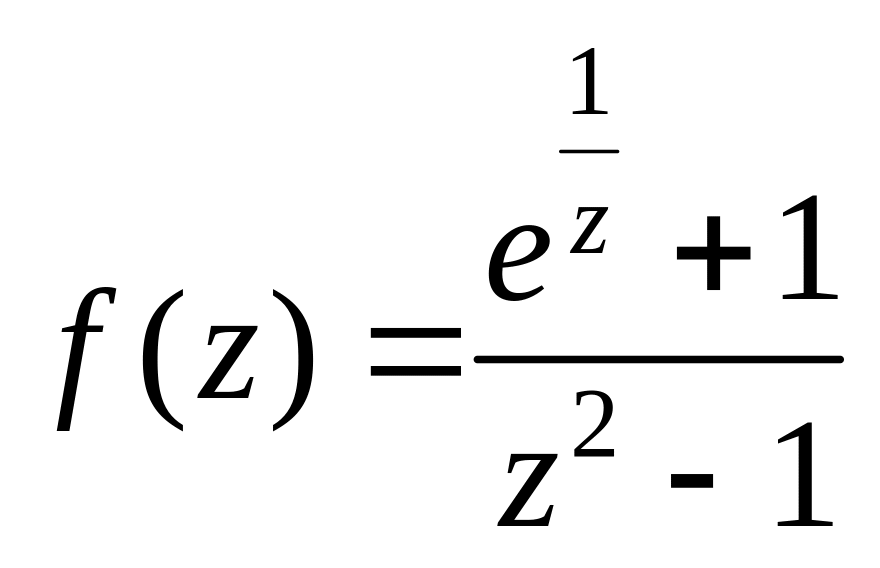 .
.
27.
![]() .
28.
.
28.
![]() .
.
29.
![]() .
30.
.
30.
![]() .
.
31.
![]() .
32.
.
32.
![]() .
.
33.
![]() .
34.
.
34.
![]() .
.
35.
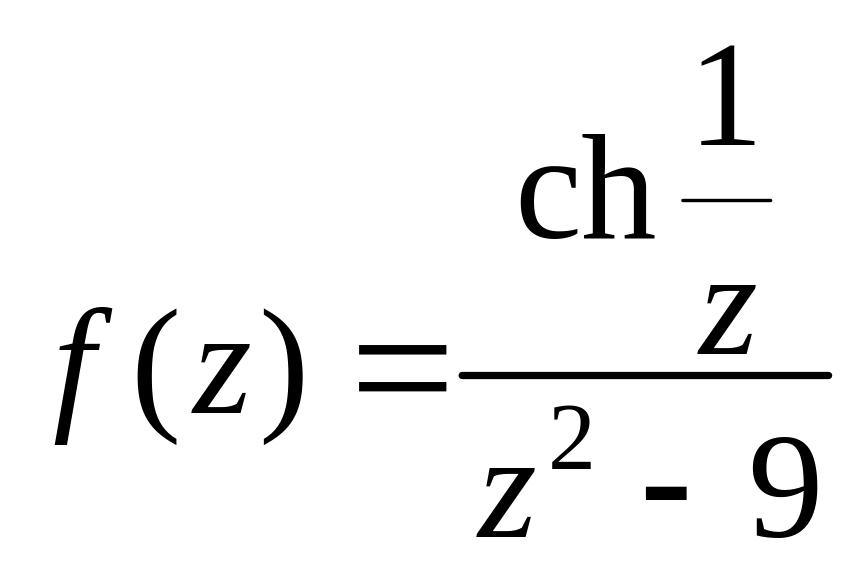 .
36.
.
.
36.
.
37.
![]() .
38.
.
38.
![]() .
.
39.
![]() .
40.
.
40.
![]() .
.
41.
![]() . 42.
. 42.
![]() .
.
5.6. Знайдіть
![]() ,
,
якщо:
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
4.
.
4.
![]() .
5.
.
5.
![]() .
.
5.7. Знайдіть
![]() ,
,
якщо:
1.
![]() .
2.
.
2.
![]() .
.
5.8. Знайдіть
![]() ,
,
якщо:
1.
.
2.
![]() .
3.
.
3.![]() .
.
5.9. Знайдіть
![]() ,
,
якщо:
1.
![]() .
2.
.
2.
![]() .
3.
.
3.![]() .
.
5.10. Знайдіть інтеграли
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
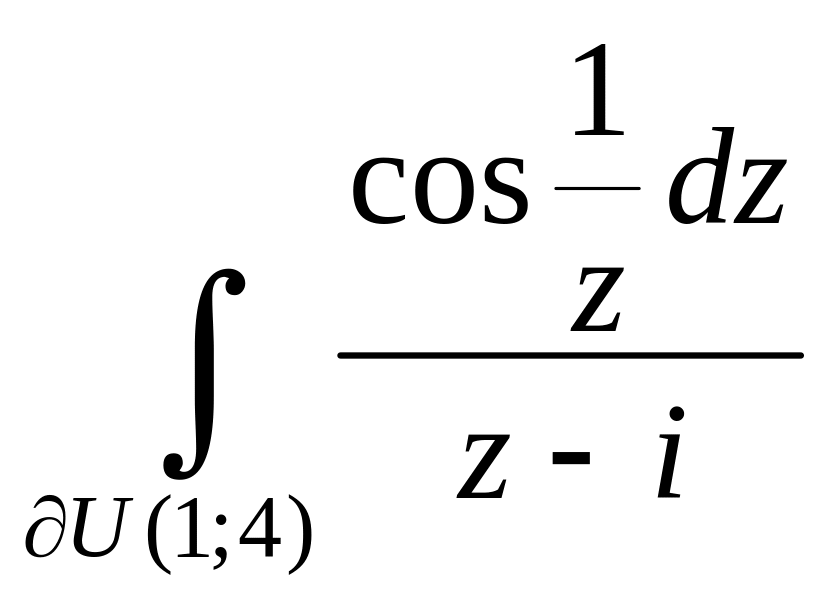 .
.
7.
![]() .
8.
.
8.
![]() .
.
9.![]() .
10.
.
10.
![]() .
.
11.
![]() .
12.
.
12.
![]() .
.
13.
![]() .
14.
.
14.
![]() .
.
15.
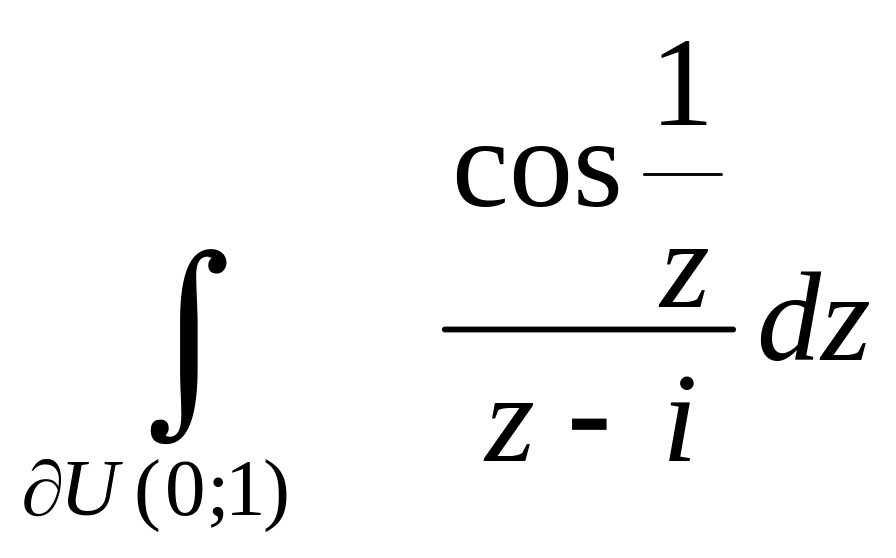 .
16.
.
16.
![]() .
.
17.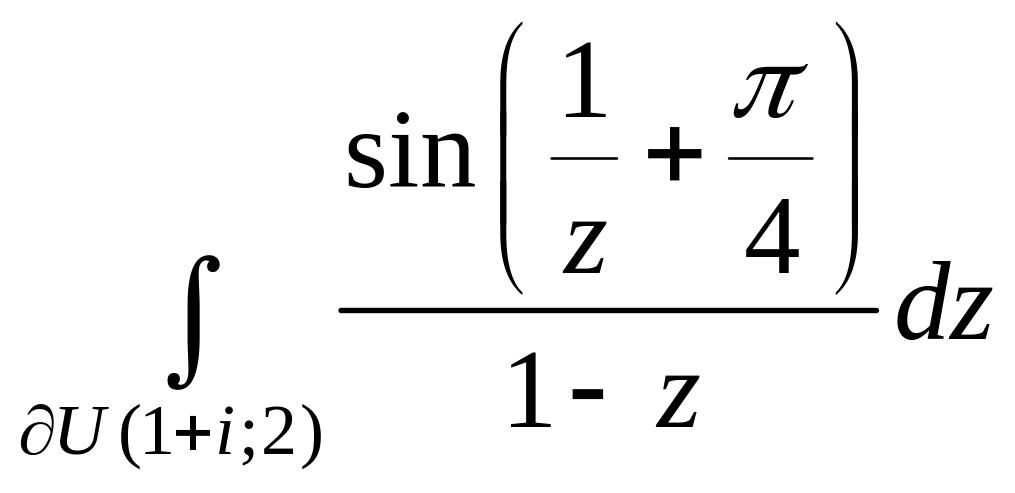 .
18.
.
18.
![]() .
.
5.11. Знайдіть інтеграли
1.
![]() .
2.
.
2.![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
7.
.
7.![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
14.
.
14.
![]() .
.
15.
![]() .
16.
.
16.![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
26.
![]() .
.
27.
![]() .
.
28.
![]() .
.
29.
![]() .
.
30.
![]() трикутник
з вершинами в точках 3i,3,-3i.
трикутник
з вершинами в точках 3i,3,-3i.
5.12. Використовуючи лишок в , знайдіть інтеграли
1.![]() .
2.
.
2.
![]() .
.
3.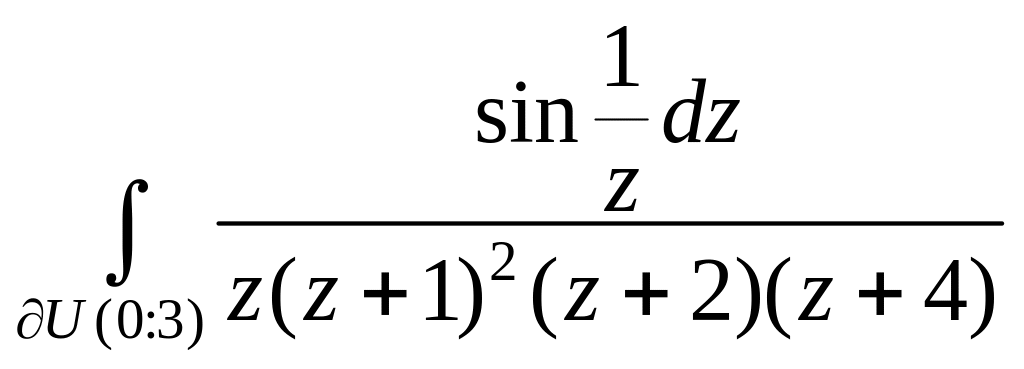 .
4.
.
4.
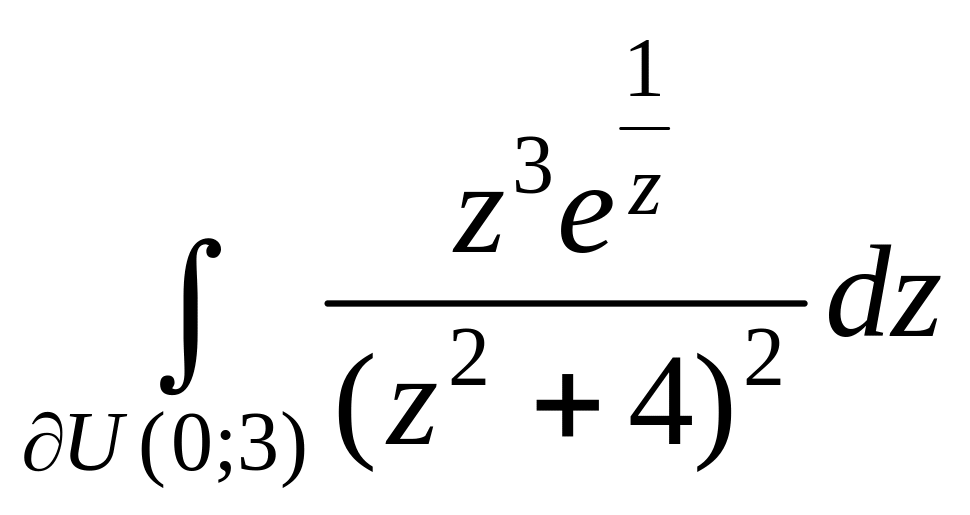 .
.
5.
![]() .
6.
.
6.
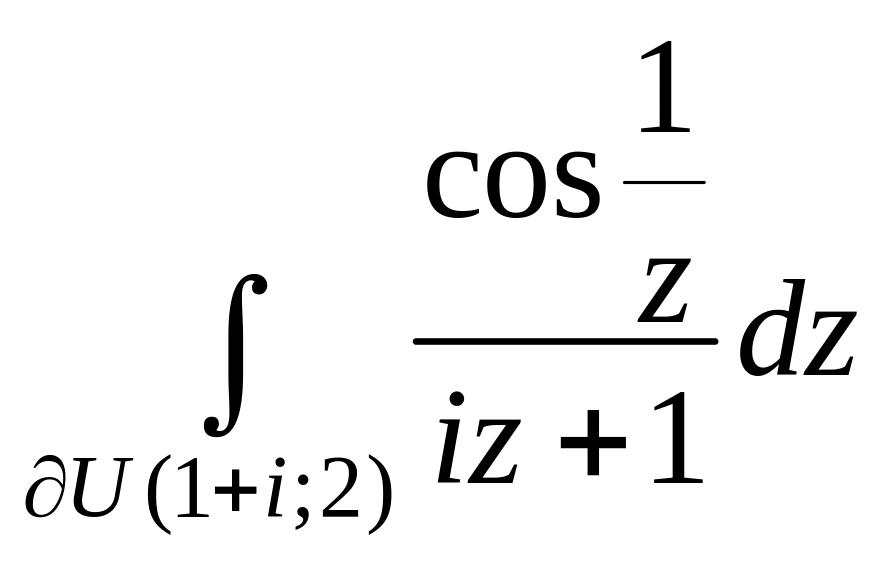
5.13. Знайдіть інтеграли
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
.
7.![]() .
8.
.
8.
![]() .
.
9.
![]() .
10.
.
10.![]() .
.
11.
![]() .
12.
.
12.
![]() .
.
13.
![]() .
14.
.
14.
![]() .
.
15.
![]() .
16.
.
16.
![]() .
.
17.
![]() .
18.
.
18.
![]() .
.
19.
![]() .
20.
.
20.
![]() .
.
21.
![]() .
.
5.13. Знайдіть інтеграли
1.![]() .
2.
.
2.![]() .
.
3.![]() .
4.
.
4.![]() .
.
5.![]() .
6.
.
6.![]() .
.
7.
![]() 8.
8.
![]() .
.
9.
![]() .
10.
.
10.
![]() .
.
11.![]() .
12.
.
12.
![]() .
.
13.
![]() .
14.
.
14.
![]() .
.
15.
![]() .
16.
.
16.
![]() .
.
17.
![]() .
18.
.
18.
![]() .
.
19.![]() .
20.
.
20.
![]()
21.
![]() .
22.
.
22.
![]() .
.
23.![]() .
24.
.
24.![]() .
.
25.![]() .
26.
.
26.
![]()
27.![]() .
28.
.
28.
![]() .
.
29.
![]() .
30.
.
30.
![]() .
.
31.
![]() .
32.
.
32.
![]()
5.14. Знайдіть інтеграли
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]()
7.
![]() .
8.
.
8.
![]() .
.
9.
![]() .
10.
.
10.![]() .
.
11.
![]() .
12.
.
12.
![]() .
.
13.
![]() .
14.
.
14.
![]() .
.
15.
![]() ,
,
![]() .
16.
.
16.![]() .
.
17.![]() .
18.
.
18.![]() .
.
19.![]() .
20.
.
20.![]() .
.
21.![]() ,
,
![]() .
22.
.
22.![]()
5.15. Доведіть наступні твердження:
1.
Нехай
![]() ,
–
скінчена множина точок із
,
які не лежать на
,
функція
є голоморфною області
і
,
коли
.
Тоді
,
–
скінчена множина точок із
,
які не лежать на
,
функція
є голоморфною області
і
,
коли
.
Тоді
![]() ,
,
де
,![]() ,
.
,
.
2.
Нехай
,
–
скінчeна
множина точок з
,
які
не лежать на
,
![]() –
скінчена множина
точок, які лежать на
–
скінчена множина
точок, які лежать на
![]() ,
функція
є голоморфною області
,
функція
є голоморфною області
![]() і
,
коли
.
Тоді
і
,
коли
.
Тоді
![]()
![]() ,
,
де
![]() ,
,
.
,
,
.
3.
Нехай
![]() –
деяка
область,
–
деяка
область,
![]() – деяка
скінчена або зліченна множина точок із
,
яка
не має в
граничних
точок,
– деяка
скінчена або зліченна множина точок із
,
яка
не має в
граничних
точок,
![]() –послідовність
областей таких, що
–послідовність
областей таких, що
![]()
![]() ,
,
![]() ,
функція
є
голоморфною в
і
,
функція
є
голоморфною в
і
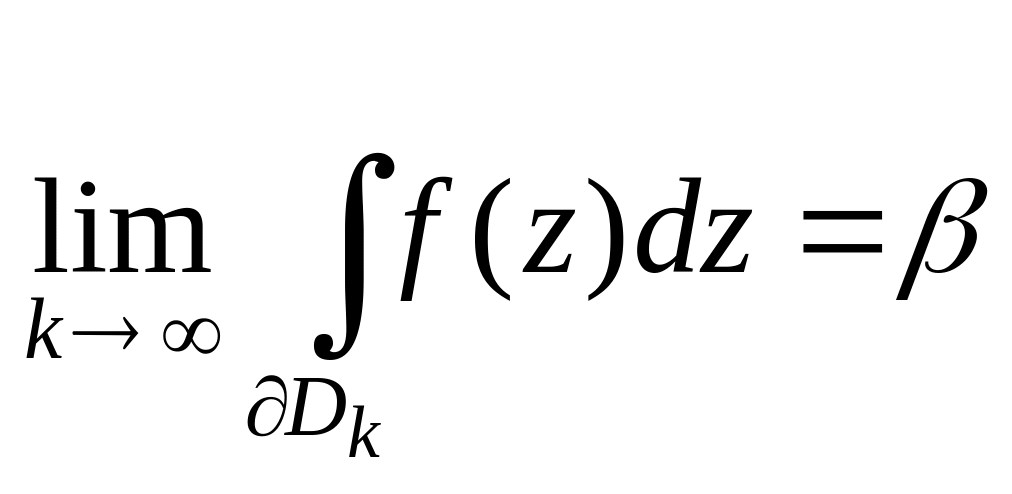 .
(1)
.
(1)
Тоді
![]() .
.
4.
Нехай
![]() – скінчена
множина комплексних чисел, які не є
цілими,
–
функція,
голоморфна в
– скінчена
множина комплексних чисел, які не є
цілими,
–
функція,
голоморфна в
![]() ,
для
якої
,
для
якої
![]() .
(2)
.
(2)
Тоді
![]() .
.
5.
Нехай
– раціональна
функція, всі полюси
![]() якої
не є цілими числами, і
.
Тоді
якої
не є цілими числами, і
.
Тоді
![]() .
.
6. Нехай – скінчена множина комплексних чисел, які не є цілими, –функція, голоморфна в , для якої
![]() .
.
Тоді
![]() .
.
7.
Нехай
– раціональна
функція, всі полюси
якої
не є цілими числами, і
![]() .
Тоді
.
Тоді![]() .
.
8.
Нехай
– раціональна
функція, яка має полюс тільки в точці
![]() ,
і
.
Тоді
,
і
.
Тоді
![]() ,
,
![]() .
.
9.
Нехай
функція
є
голоморфною в півплощині
![]() ,
неперервною
,
неперервною
![]() і
для деякого
і
для деякого
![]() виконується
виконується
![]() .
.
Тоді
для кожного
![]() виконується
виконується
![]()
![]()
5.16. Обґрунтуйте формули
1.
![]() ,
,
![]() .
.
2.
![]() ,
.
,
.
3.
![]() .
4.
.
4.
![]() .
.
5.17. Обґрунтуйте формули
1.![]() .
2.
.
2.![]() .
.
3.![]() .
4.
.
4.![]() .
.
5.![]() .
6.
.
6.![]() .
.
7.![]() .
8.
.
8.![]() .
.
9.![]() .
10.
.
10.![]() .
.
11.![]() .
12.
.
12.![]() .
.
13.![]() .
.
5.18. Розв’яжіть задачу Коші
1.![]() ,
,
.
2.
,
,
.
2.![]() ,
,
.
,
,
.
3.![]() ,
,
.
4.
,
,
.
4.![]() ,
,
.
,
,
.
5.![]() ,
,
![]() ,
,
![]() .
6.
,
,
.
.
6.
,
,
.
