Приклад 1. Згідно зі сказаним вище, якщо , то

.

Підінтегральна функція має особливі точки

,

і тільки належить . Тому

.

Приклад 2. Обчислимо

.

За попередніми міркуваннями і, оскільки z=0 є полюсом сьомого порядку функції , то

.

4. Знаходження деяких невласних інтегралів.

Лема 1. Нехай функція є неперервною в усіх точках півплощини , за винятком скінченного числа точок . Тоді, якщо

(1)

то

.

Доведення. Справді,

, .►

Нагадаємо, що інтегралом в розумінні головного значення функції в точках , де і для всіх , називається границя

,

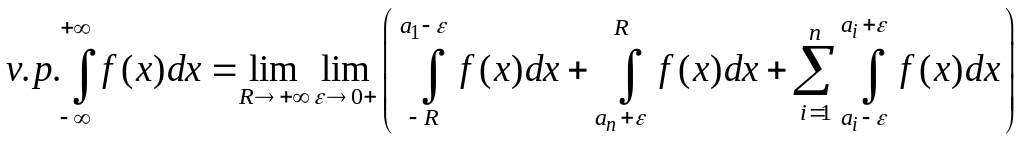де справа стоять інтеграли Рімана. Якщо функція інтегрована на у невласному розумінні, то вона також інтегрована на в розумінні головного значення і обидва інтеграли збігаються. Для позначення розглядуваного інтеграла використовують також символи

, .

Терема 1. Нехай функція є голоморфною в і неперервною в , де - деякі точки з . Тоді, якщо виконується (1), то

Доведення. Справді, візьмемо таке , щоб всі точки лежали в області . Застосувавши до основну теорему про залишки, отримуємо

і залишилось скористатись лемою 1. ►

Приклад 1. Для знаходження інтегралу

розглянемо функцію . Вона є голоморфною в , має в точці простий полюс і задовольняє умову (1) для . Тому

.

5. Лема Жордана.

Теорема 1 (лема (Жордана). Нехай функція є неперервною в за винятком скінченого числа точок

. (1)

Тоді для кожного

. (2)

Доведення. Маємо

де . Оскільки для , то

.

Тому, враховуючи що

,

отримуємо

►

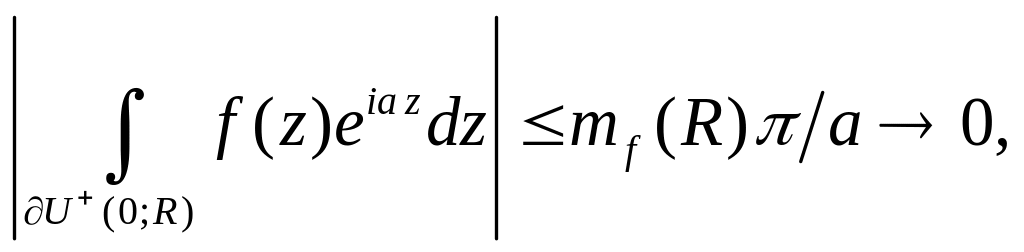
Приклад 1. Для знаходження інтегралу розглянемо функцію . Нехай . Проводячи міркування аналогічні тим, що були використані при доведені леми Жордана, отримуємо

Справді,

,

а

.

Крім цього,

Тому, враховуючи те, що функція є цілою, то за інтегральною теоремою Коші

А, оскільки , то

Отже,

6. Знаходження інтегралів v.p. .

Теорема 1. Нехай , , – скінчена кількість точок із півплощини , функція є голоморфною в області задовольняє умову (1) попереднього пункту і в тих точках , для яких , має прості полюси. Тоді

. (1)

Доведення. Застосуємо до областей

,

основну теорему про залишки. Тоді

,

.

З іншого боку,

,

. (2)

Звідси випливає

.

Додавши почленно останні дві рівності, перейшовши до границі при і та скориставшись лемою Жордана і тим фактом, що для тих , для яких , виконується

,

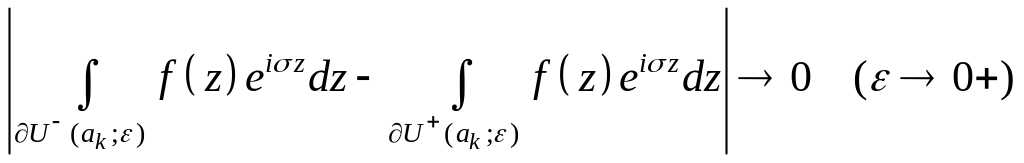приходимо до потрібного висновку. ►

Наслідок 1. Якщо задовольняє умови теореми 2 і для , то для кожного

,

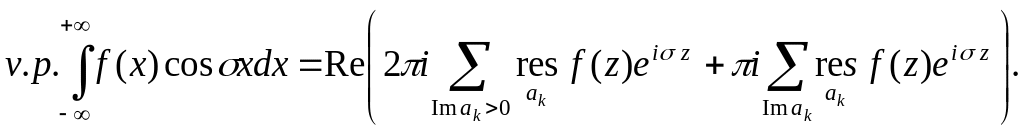
Зауваження. У випадку, коли , f задовольняє умови леми Жордана в (в (2) інтегрування ведеться по ), справедливою є формула

.

Приклад 1.

Приклад 2.

.

Приклад 3.

.