Лабораторная работа №6 Компьютерное моделирование случайных процессов. Краткие теоретические сведения.

Стохастические математические модели. Математическая модель – это связь между исходными данными и результатами, выраженная в математическими формулами, уравнениями и т.п. Символически математическая модель может быть записана так:

Y=F(x₁,x₂,…,x_n)

Если все x_j, входящие в правую часть, т.е. все исходные данные модели являются однозначно определенными, то модель называется детерминированной, если среди них есть случайные величины, то – стохастической. При этом меняются цели построения моделей. Вместо вопросов типа «Чему равно значение выходного параметра» задают вопросы типа «С какой вероятностью выходной параметр принимает то или иное значение?», «Каково математическое ожидание данного параметра?» и т.п. Проводя численный эксперимент, выполняют очень большое число испытаний и статистическую обработку их результатов. Напрмер, можно не вычислять численность популяций, а изо дня в день, из года в год вести наблюдение за этой численностью и проведя их статистическую обработку, получить некоторый аналитический вид зависимости.

Генерирование случайных чисел на компьютере. При компьютерном математическом моделировани случайных процессов нельзя обойтись без наборов случайных чисел, удовлетворяющих заданному закону распределения. Стандартная функция random() языка Pascal генерирует дробные случайные числа, равномерно распределенные на отрезке (0,1) .Это значит, что если разбить отрезок (0,1) на несколько равных промежутков, то вероятность попадания случайного числа в один из промежутков примерно одинаковая. Функция random(N) дает также равномерно распределенные целые случайные числа от 0 до N-1 включительно. Аналогичные результаты можно получить в табличном процессоре Excel с помощью функций СЛЧИС() и СЛУЧМЕЖДУ(A,B) соответственно. Однако равномерное распределение не всегда хорошо отражает реальность. Если игральная кость может упасть одной из своих граней с одинаковой вероятностью, то интервалы времени между приходами покупателей в магазин подчиняются другому закону распределения ( какой-то интервал встречается с максимальной частотой, чем дальше от этого значения, тем частоты ближе к 0). Например, семейство функций Пуассона хорошо отражают характер такого распределения:

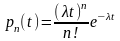
Такие функции имеют максимум при t=n/ и нормированны. В Excel такое распределение можно получить с помощью надстройки «Анализ данных», выбрав «Генерацию случайных чисел», «распределение Пуассона» и введя необходимые Рис.1 График функции P_n(t) значения параметров.

Некоторые случайные процессы.

Процессы массового обслуживания. К числу случайных процессов, изучаемых методом имитационного моделирования относятся, в частности, процессы, связанные с формированием и обслуживанием очередей. Простейшая задача данного класса такова. Имеется система массового обслуживания с одним узлом обслуживания (магазин с одним продавцом, ремонтная зона в автохозяйстве, травмпункт с одним врачом, телефонная станция с одним входом, сервер с одним входным каналом и т.д.). К услугам системы клиенты прибегают случайным образом (с заданной функцией распределения отрезков времени между приходами). Если система свободна, то начинает обслуживать клиента сразу, иначе ставит его в очередь. Длительность обслуживания каждого клиента — случайная величина с известным законом распределения.

В ходе решения данной задачи требуется дать ответ на вопросы типа: какова функция распределения вероятностей времени ожидания клиента в очереди? Времени простоя системы в ожидании клиентов? Если сами эти функции определять сложно, то каковы их наиболее важные характеристики (т.е. математическое ожидание, дисперсия и т.д.)?

Задача Бюффона. Французский натуралист, биолог, математик, естествоиспытатель и писатель XVIII века Жорж-Луи Леклерк де Бюффон аналитически нашел, что если на поле, разграфленное параллельными прямыми, расстояние между которыми L, бросается наугад игла длиной l, то вероятность того, что игла пересечет хотя бы одну прямую, определяется формулой . Эта задача дала способ имитационному определению числа . Действительно, если L=2l, то .

«Бросок иглы» моделируется генерированием трех случайных чисел – координат одного из концов иглы X,Y и угла наклона иглы к положительному направлению оси абсцисс α. Координаты второго конца иглы вычисляются из прямоугольного треугольника с гипотенузой l и острым углом α (или π-α). Для простоты можно считать, что прямые проведены через точки 0, 1, 2, … Тогда условием пересечения иглой какой-либо прямой будет неравенство целых частей ординат концов иглы.

Процесс случайного одномерного блуждания (модель «пьяницы»). В начальный момент времени точка находится на нулевой отметке числовой прямой. Блуждание задается по правилу: если случайное число из отрезка [0,1] меньше 0,5, то делается шаг вправо на расстояние h, в противном случае  влево. Распределение случайных чисел принимается равновероятным. Обычно ставятся следующий вопрос: какова вероятность удаления точки на расстояние k от начального положения через n шагов. Обобщение данной модели на плоскость и на большое количество точек позволяет моделировать процессы, происходящие в жидкостях и газах.

Пример выполнения задания

Задача. На междугородней телефонной станции две телефонистки обслуживают общую очередь заказов. Очередной заказ обслуживает та телефонистка, которая первой освободилась. Если обе в момент поступления заказа заняты, то звонок аннулируется. Смоделировать процесс, считая входной поток пуассоновским, а длительность обслуживания постоянной.

Решение. В задаче требуется смоделировать систему массового обслуживания с двумя каналами, с отказами. Время будем измерять в минутах. Длительность обслуживания заявки каждой из телефонисток примем равным 0,2 и поместим это значение в ячейку I2 (Рис.2). В качестве случайной величины возьмем интервал времени между поступлением заявок.

В диапазоне B2:B101 получены целые случайные числа, распределенные по пуассоновскому закону (Данные-Анализ данных- Генерация случайных чисел- Число переменных=1, Число случайных чисел=100, Распределение= Пуассона, Лямбда=10, Выходной интервал=$B$2- OK). В диапазоне С2-С101 –те же числа, поделенные на 100 с тем, чтобы сделать интервалы времени дробными. В ячейке D3 – формула =D2+C3 для вычисления момента поступления очередного звонка. В ячейку E3 введем условие, при котором звонок обслуживается первой телефонисткой: =ЕСЛИ(МАКС($E$2:E2)<D3; D3+$I$2;0) , в ячейку F3 – условие обслуживания звонка второй телефонисткой: =ЕСЛИ(И(МАКС($F$2:F3)<D4;E4=0);D4+$I$2;0). В ячейках G3 и H3 проверяется, обслужена заявка или нет: =ЕСЛИ(И(E3=0;F3=0);0;1) и =ЕСЛИ(И(E4=0;F4=0);1;0) соответственно. Введенные формулы копируются на весь диапазон.

Рис.2 Начало таблицы, моделирующей работу системы с отказами

Пронаблюдав за системой в течение примерно 10 минут (ячейка D101 на рис.3), делаем вывод: при выбранных значениях входных параметров система обслуживает 77% поступающих заявок.

Рис.3 Конец таблицы. В ячейках G102 и H102 получены выходные параметры модели: количество обслуженных заявок и количество отказов.