Задание к лабораторной работе

4. В среде Lazarus имитировать движение тела согласно варианту лабораторной работы №2.

5. Исследовать зависимость характера движения от параметров модели.

6. Создать текстовый отчет по лабораторным работам №2-4, включающий:

• постановку задачи и описание модели;

• результаты тестирования программы;

• результаты, полученные в ходе выполнения заданий (в различных формах);

• качественный анализ результатов.

Лабораторная работа №5 Компьютерное моделирование в экологии Краткие теоретические сведения

В данной работе рассматриваются лишь модели классической экологии (взаимодействие популяций).

Популяция  совокупность особей одного вида, существующих в одно и то же время и занимающих определенную территорию.

Взаимодействие особей внутри популяции определяется внутривидовой конкуренцией, взаимодействие между популяциями  межвидовой конкуренцией.

Внутривидовая конкуренция в популяции с дискретным размножением. Для популяций с дискретным размножением (некоторые виды растений, насекомых и т.д.) поколения четко разнесены во времени и особи разных поколений не сосуществуют. Численность такой популяции можно характеризовать числом N_t и считать t величиной дискретной  номером популяции.

Одна из моделей межвидовой конкуренции в этом случае выражается уравнением

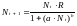(1)

Здесь R  скорость воспроизводства популяции в отсутствии внутривидовой конкуренции (математически это соответствует случаю a = 0). Тогда уравнение определяет просто изменение численности популяции по закону геометрической прогрессии: 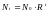, где N₀  начальная численность популяции.

Знаменатель в уравнении (1) отражает наличие конкуренции, делающей скорость роста тем меньше, чем больше численность популяции; a и b  параметры модели.

Исходные параметры модели:

 R  скорость воспроизводства;

 N₀  начальная численность популяции;

 a  параметр, характеризующий интенсивность внутривидовой конкуренции.

Характерная черта эволюции при b=1  выход численности популяции на стационарное значение при любых значениях других параметров. Однако, в природе так бывает не всегда, и более общая модель при b1 отражает другие, более сложные, но реально существующие, виды эволюции. Данная модель позволяет получить четыре таких вида:

1. монотонное установление стационарной численности популяции;

2. затухающие колебания и установление стационарной численности популяции;

3. устойчивые предельные циклы изменения численности популяции;

4. случайные изменения численности популяции без наличия явных закономерностей (динамический хаос).

Внутривидовая конкуренция в популяции с непрерывным размножением. Математическая модель в данном случае строится на основе дифференциальных уравнений. Наиболее известна так называемая логистическая модель:

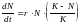₍₂₎

Исходные параметры модели:

 r  скорость роста численности популяции в отсутствие конкуренции;

 K  предельное значение численности популяции, при котором скорость роста становится равной нулю;

 N₀  начальная численность популяции.

Межвидовая конкуренция. В этом случае исследуется конкуренция популяций, потребляющих общий ресурс. Пусть N₁ и N₂  численности конкурирующих популяций. Модель (называемая также моделью Лотки-Вольтерры) выражается уравнениями

(3)

Содержательный смысл параметров: r₁ и r₂ – скорости роста численности первой и второй популяций соответственно в отсутствие конкуренции; β₁ и β₂ – коэффициенты, учитывающие внутривидовую конкуренцию; ₁ и ₂ отражают интенсивность межвидовой конкуренции.

Главный вопрос, который интересует исследователя межвидовой конкуренции  при каких условиях увеличивается или уменьшается численность каждого вида? Данная модель предсказывает следующие режимы эволюции взаимодействующих популяций: устойчивое сосуществование или полное вытеснение одной из них.

Система «хищник-жертва». В этой системе ситуация значительно отличается от предыдущей. В частности, если в случае конкурирующих популяций исчезновение одной означает выигрыш для другой (дополнительные ресурсы), то исчезновение «жертвы» влечет за собой и исчезновение «хищника», для которого в простейшей модели «жертва» является единственным кормом.

Обозначим через С численность популяции хищника и через N  популяции жертвы. Одна из известных моделей выражается следующими уравнениями:

(4)

В первое уравнение заложен следующий смысл. В отсутствии хищников (т.е. при С=0) численность жертв растет экспоненциально со скоростью α, т.к. модель не учитывает внутривидовой конкуренции. Число жертв уменьшается тем больше, чем чаще происходят встречи представителей видов; γ  коэффициент эффективности поиска.

Второе уравнение говорит о следующем. В отсутствии жертв численность хищников экспоненциально убывает со скоростью β; положительное слагаемое в правой части уравнения компенсирует эту убыль; δ  коэффициент эффективности перехода пищи в потомство хищников.

Пример выполнения задания

Задача. Реализовать моделирование межвидовой конкуренции при фиксированных значениях начальной численности популяций 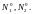Проанализировать зависимость судьбы популяций от соотношения значений параметров r₁, r₂, β₁, β₂, α₁, α₂.Выяснить, при каких условиях обе популяции выживают.

В качестве математической модели межвидовой конкуренции примем формулы (3). Исследуем модель путем нахождения особых точек на фазовой плоскости (N₁ON₂) ([6]). Как известно, судьбы популяций зависят от соотношения параметров r₁, r₂, β₁, β₂, α₁, α₂, а именно, обе популяции выживают, если на фазовой плоскости существует особая точка- устойчивый узел- c координатами . При этом выполняются следующие соотношения: . Выберем значения параметров r₁, r₂, α₁, α₂ произвольно (имея в виду, что r₁, r₂ – это числа, означающие скорость роста популяции в отсутствие конкуренции и должны иметь значения, большие единицы, а α₁, α₂ характеризуют конкуренцию, т.е. вероятность гибели особи при встрече с другой особью и должны быть меньше единицы), а параметры β₁, β₂ получим из соотношений 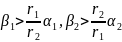. Начальные значения численности популяций возьмем, например, больше, чем координаты особой точки. Для построения таблицы значений N₁ и N₂ воспользуемся методом Эйлера решения дифференциальных уравнений (3). Из таблицы и диаграммы видно, что численности популяций уменьшаются, стремятся к особой точке и обе популяции выживают (Рис.1).

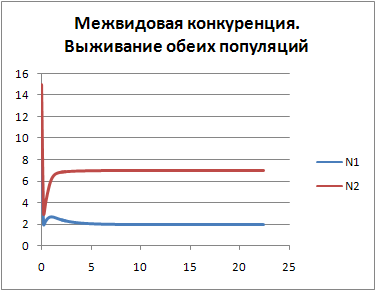
Р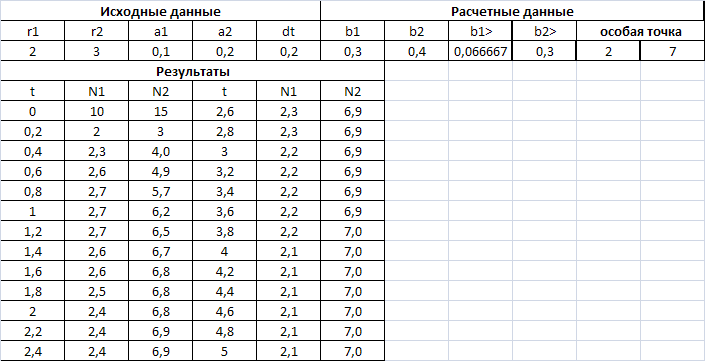 ис.1 При заданных значения входных параметров обе популяции выживают

Задание к лабораторной работе

1. Выписать математическую модель, определить состав набора входных параметров и их конкретные числовые значения.

1. Спроектировать таблицу для представления результатов моделирования, предусмотрев в ней области ввода исходных данных, параметров модели и вывода результатов.

2. Выбрать метод интегрирования дифференциальных уравнений модели, разработать самостоятельно табличный алгоритм интегрирования с заданной точностью.

1. Произвести отладку и тестирование алгоритма в среде табличного процессора.

1. Выполнить конкретное задание из своего варианта работы.

1. Качественно проанализировать результаты моделирования.

1. Создать текстовый отчет по лабораторной работе, включающий:

• постановку задачи и описание модели;

• результаты тестирования программы;

• результаты, полученные в ходе выполнения задания (в различных формах);

• качественный анализ результатов.

Варианты заданий.

Вариант 1.

Изучить характер эволюции популяции, описываемый моделью (1), при фиксированных значениях параметров b, R, N₀ в зависимости от значения параметра а. Подобрать значения а, дающие качественные различия в характере эволюции.

Вариант 2.

Изучить характер эволюции популяции, описываемый моделью (1), при фиксированных значениях параметров a, R, N₀ в зависимости от значения параметра b в диапазоне. Подобрать значения b , дающие качественные различия в характере эволюции.

Вариант 3.

Изучить характер эволюции популяции, описываемый моделью (1), при фиксированных значениях параметров a, b, N₀ в зависимости от значения параметра R . Подобрать значения R , дающие качественные различия в характере эволюции.

Вариант 4.

Для модели (1) найти сочетания значений параметров b и R, дающих режимы монотонного и колебательного установления стационарной численности популяции изучаемой системы. Прочие параметры модели фиксированы.

Вариант 5.

Для модели (1) сочетания значений параметров b и R, дающих режим колебательного установления стационарной численности популяции изучаемой системы и режим устойчивых предельных циклов. Прочие параметры модели фиксированы.

Вариант 6.

Реализовать моделирование межвидовой конкуренции по формулам (3) при фиксированных значениях параметров r₁, r₂, β₁, β₂, α₁, α₂. Проанализировать зависимость судьбы популяций от соотношения значений их начальной численности

Вариант 7.

Реализовать моделирование межвидовой конкуренции по формулам (3) при значениях параметров r₁, r₂, β₁, β₂, 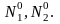. Проанализировать зависимость судьбы популяций от соотношения значений коэффициентов конкуренции ₁ и  ₂.

Вариант 8.

Подобрать значения обеспечивающие какие-либо два режима эволюции конкурирующих популяций (в соответствии с моделью (3)). Остальные параметры модели выбрать произвольно.

Вариант 9.

Провести моделирование динамики численности популяций в системе «хищник-жертва» (модель (4)) при фиксированных значениях параметров α, β, γ, δ. Проанализировать зависимость исхода эволюции от соотношения значений параметров N₀ и C₀.

Вариант 10.

Провести моделирование динамики численности популяций в системе «хищник-жертва» (модель (4)) при фиксированных значениях параметров α, β, γ, N₀, C₀. Проанализировать зависимость результатов моделирования от значения параметра δ.

Вариант 11.

Провести моделирование динамики численности популяций в системе «хищник-жертва» (модель (4)) при фиксированных значениях параметров α, β, δ, N₀, C₀. Проанализировать зависимость результатов моделирования от значения параметра γ .

Вариант 12.

Провести моделирование динамики численности популяций в системе «хищник-жертва» (модель (4)) при фиксированных значениях параметров β, γ, δ, N₀, C₀ . Проанализировать зависимость результатов моделирования от значения параметра α.