Потенциальная энергия при сдвиге

Потенциальную энергию при сдвиге можно определить аналогично тому, как это было сделано при растяжении. Работа сдвигающей силы равна:

.

Выразив  из формулы (3.5), получим:

.

(3.9)

Поделив полученное значение потенциальной энергии на объём (V₀=aS), получим значение удельной потенциальной энергии при сдвиге:

.

(3.10)

Понятие о смятии

Деформация сдвига часто сопровождается смятием – местными сжатиями материала в зоне контакта соприкасающихся тел, вызванными действием значительного давления в зоне контакта. Из двух соприкасающихся деталей вероятность местного сжатия больше для материала более мягкого. Назовём давление в зоне контакта условно напряжением смятия.

.

S_см – площадь смятия, условно равное проекции поверхности контакта на плоскость, перпендикулярную действующей силе.

Расчет заклепочного соединения на прочность

Заклёпочное соединение осуществляется с помощью специальных деталей заклёпок. Заклёпки в соединении, находящемся под действием продольных сил, рассчитываются на срез:

,

(3.11)

где n - количество заклепок, m - число плоскостей среза.

Кроме расчета на срез проводят расчёт на смятие:

,

(3.12)

где t – толщина соединяемых деталей.

Е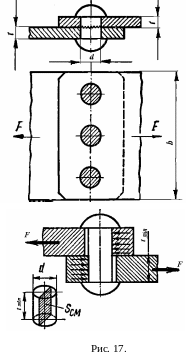 сли соединяемые детали имеют различную толщину, то расчёт на смятие проводят по детали с наименьшей толщиной.

Наличие заклёпок вносит некоторые изменения в проверку прочности самих склёпанных листов. Опасным сечением каждого листа (рис. 17) будет сечение, ослабленное заклёпочными отверстиями, поэтому кроме проверки на прочность самой заклёпки проводят расчет листа на разрыв:

,

(3.13)

где b – ширина листа.

Лекция 4 Геометрические характеристики плоских сечений

В инженерных задачах часто приходится определять центры тяжести и геометрические характеристики различных сечений тел.

Центром тяжести плоского сечения называется точка с координатами

,	(4.1)
,

где y_i и z_i – координаты i – ой площадки, S_i – площадь i – ой площадки.

В общем виде геометрические характеристики поперечного сечения выражаются интегралом

1. При m=0; n=0 - - площадь сечения.

2. При m=1; n=0 - - статический момент площади сечения относительно оси z.

При m=0; n=1 - - статический момент площади сечения относительно оси y.

При m=1; n=1 - - центробежный момент инерции сечения.

При m=2; n=0 - - осевой момент инерции сечения относительно оси z.

П ри m=0; n=2 - - осевой момент инерции сечения относительно оси y.

- полярный момент инерции.

Расстояние  от любой элементарной площадки до начала координат связано с расстоянием этой площадки до осей координат y и z зависимостью:

Тогда полярный момент инерции сечения можно представить в виде суммы осевых моментов инерции относительно двух взаимно перпендикулярных осей:

Jp = Jz + Jy.

(4.2)

геометрические характеристики J_y; J_z и A могут быть только положительными, а S_y, S_z и J_yz – как положительными, так и отрицательными.

Величины всех геометрических характеристик зависят от форм и размеров плоской фигуры, а S_y, S_z, J_y, J_z, J_yz, кроме того, и от расположения координатных осей Y и Z .

Сумма осевых моментов инерции площади фигуры относительно двух взаимно перпендикулярных осей есть величина постоянная, не зависящая от поворота осей и равная полярному моменту инерции площади этой фигуры относительно начала координат. При вычислении геометрических характеристик оси Y и Z называют осями инерции.

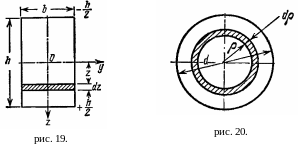
Найдем осевой момент инерции для прямоугольного сечения (рис. 19):

,

(4.3)

аналогично:

.

(4.4)

Полярный момент инерции круглого сечения (рис. 20).

.

(4.5)

Для круглого сечения J_p = J_z + J_y, причем .