Н апряжения при плоском напряженном состоянии
Рассмотрим прямоугольный параллелепипед, на боковые грани которого действуют главные напряжения 1 и 2 (рис. 40).
Проведём сечение, нормаль n к которому составляет с осью I угол , а с осью II угол (+90О). Нормальные напряжения в этом сечении
|
(6.9) |
|
(6.10) |
,
.Напряжение по площадке, перпендикулярной первой, имеющей нормаль n (=+90), составит:
|
(6.11) |
|
(6.12) |
,
.Тогда:
,
.
Т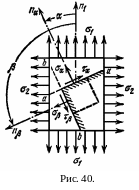
.е.
сумма нормальных напряжений по двум
взаимно перпендикулярным площадкам
постоянна и равна сумме главных
напряжений:
|
(6.13) |
.Для касательных напряжений, имеем:
|
(6.14) |
.Следовательно, касательные напряжения по двум взаимно перпендикулярным площадкам равны по величине и противоположны по знаку. Это свойство называют законом парности касательных напряжений, оно имеет место во всех случаях, когда имеются касательные напряжения.
Лекция 7 Понятие о теориях прочности
Нахождение значений опасных напряжений, представляющих основу для назначения допускаемых напряжений, в случае линейного напряжённого состояния не представляет затруднений. При сложном напряжённом состоянии, характеризующимся в общем случае тремя различными главными напряжениями, нахождение опасных значений этих напряжений сильно усложняется. Как показывают опыты, опасное состояние элемента конструкции зависит от вида напряжённого состояния, то есть от соотношений между тремя главными напряжениями, но число различных возможных соотношений между ними неограниченно велико.
Поэтому требуется найти способ составления условия прочности при сложном напряжённом состоянии, пользуясь величинами т и в, полученными для линейного напряжённого состояния, зная 1, 2, 3 и сохраняя тот же коэффициент запаса прочности К.
Поставленная задача может быть решена только на основании гипотезы о том, какой вид имеет функция, связывающая прочность материала с величиной и знаком главных напряжений:
|
(7.1) |
.Опасное состояние, как для пластичных, так и для хрупких материалов, с достаточным для практики приближением, лежит на границе применения закона Гука, что позволяет использовать зависимости, полученные ранее.
Теория наибольших нормальных напряжений (первая теория прочности)
В качестве критерия прочности принимается наибольшее растягивающее напряжение. По этой теории прочности разрушение материала, независимо от вида напряженного состояния, произойдёт при условии:
,
где отр - постоянное для данного материала сопротивление отрыву.
Тогда, очевидно, условие прочности по этой теории будет иметь вид:
|
(7.2) |
,где []p – допускаемое напряжение растяжения.
Эта теория подтверждается опытами на растяжение таких хрупких материалов, как камень, кирпич, бетон, стекло, фарфор. Недостатком этой теории является то, что она не принимает во внимание два других главных напряжения, от которых тоже зависит прочность материала, что нередко приводит к расхождению с опытами.
Теория наибольших удлинений (вторая теория прочности)
По этой теории разрушение материала независимо от вида напряженного состояния наступит, если наибольшее упругое относительное удлинение max станет равно некоторой постоянной для этого материала величине разр:
.
Если
при простом растяжении
,то
.
таким образом, при сложном состоянии разрушение произойдёт при условии, что
.
Условие прочности по этой теории имеет вид:
|
(7.3) |
.Эта теория удовлетворительно согласуется с опытами для хрупких материалов.
Обе теории, первая и вторая, являются теориями отрыва, но ни одна из них не является универсальной. Иногда лучшее совпадение даёт первая, иногда вторая теория.
Теория наибольших касательных напряжений (третья теория прочности)
По этой теории опасное состояние материала, независимо от вида напряженного состояния, наступит при условии, что наибольшее касательное напряжение max станет равным некоторой постоянной для этого материала величине.
Безопасное состояние будет, очевидно, определяться условием прочности:
|
(7.4) |
.