Концентрация напряжений

Р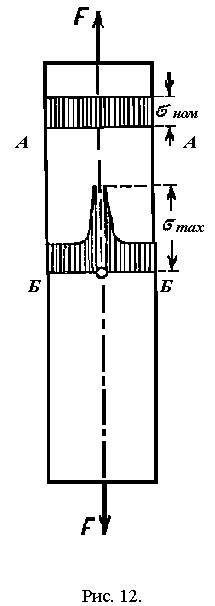 авномерное распределение напряжений по площади сечений стержня при растяжении или сжатии сохраняется лишь в однородных призматических стержнях, не имеющих внутренних или внешних повреждений и только в тех случаях, когда сечение достаточно удалено от мест приложения нагрузки. Этот характер распределения нарушается в местах приложения нагрузки, а также там, где в детали имеются разного рода отверстия, выточки, переходы от сечения одних размеров и форм к другим, какие-либо внутренние или внешние повреждения и пороки, неоднородность строения материала. Рассмотрим стержень, растянутый силами F, действующими вдоль оси (рис. 12).

В сечении А-А нормальные напряжения будут распределены равномерно. В сечении Б-Б, где в стержне имеется отверстие, распределение напряжений будет иным.

Такие повышения напряжений называются местными напряжениями Причины, вызвавшие их возникновение, называются факторами (источниками) повышения или концентрации напряжений.

Этими факторами могут быть отверстия, выточки, повреждения и т. д. Отношение наибольшего местного напряжения _max к номинальному _ном называется коэффициентом концентрации напряжений

Коэффициент концентрации зависит не только от формы детали, но и от материала образца. Он тем ниже, чем материал пластичнее.

Это объясняется тем, что пластические свойства материала образуют своеобразный буфер, снижающий в той или иной степени эффект местных напряжений.

Твёрдость и методы её определения

Твердость – способность материала противостоять внедрению в него инородных тел под действием внешних сил. Существуют несколько методов определения твёрдости. Рассмотрим два наиболее часто используемых: метод Бринеля и метод Роквелла.

Метод Бринеля. Сущность метода заключается во вдавливании шарика 2, изготовленного из закалённой высокоуглеродистой стали, в испытуемый материал 1 усилием F=29430 Н в течение определённого времени, и измерении диаметра отпечатка после снятия нагрузки (рис. 13а). В соответствии со стандартом применяются шарики диаметром 2,5; 5 и 10 мм, в зависимости от толщины образца. Твердость выражается отношением приложенной нагрузки к площади поверхности отпечатка. Измеряется твёрдость в единицах Бринеля НВ:

.

Для исключения ошибок связанных с возможной деформацией шарика, метод Бринеля применяют к материалам с твёрдостью не выше 450 НВ.

Метод Роквелла. Сущность метода заключается во вдавливании наконечника с алмазным конусом 2 в испытуемый образец 1 под действием последовательно прилагаемых (предварительной (F₀=10 Н) и основной (F=1373 Н)) нагрузок и в измерении остаточного увеличения с глубины проникновения этого наконечника на поле снятия основной нагрузки. Угол при вершине алмазного конуса =120 (рис. 13б). Твердость определяется разностью между условной максимальной глубиной проникновения индентора и остаточной глубиной его внедрения под действием основной нагрузки после её снятия, но при сохранении предварительной нагрузки. Обозначается цифрами от 20 до 67 ед., обозначающими число твёрдости и буквами HRC_э.

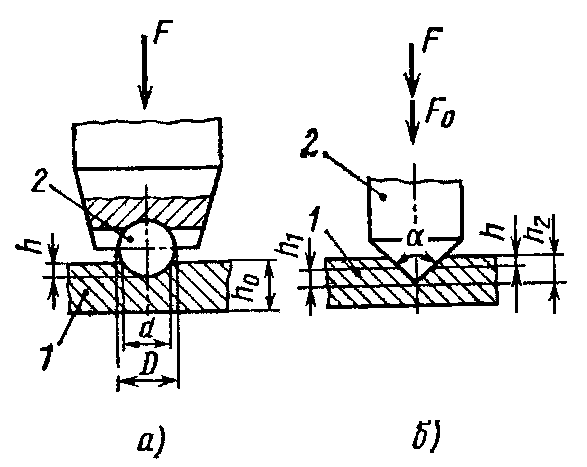
Рис. 13.

Сдвиг

Проверяя прочность растянутого или сжатого стержней, мы определяли напряжение только по сечению, перпендикулярному к его продольной оси. Но правильно оценить угрожающую прочность стержня можно лишь полностью зная его напряженное состояние. а это требует умения вычислять напряжение не только по сечению, перпендикулярному продольной оси, а по любому выбранному сечению.

Вычислим напряжение, действующее по какому-либо наклонному сечению. Рассмотрим призматический стержень, нагруженный растягивающими силами F (рис. 14). разделим его на две части поперечным сечением А1-А1 составляющим угол  с поперечным сечением А-А п ерпендикулярным продольной оси стержня. Применяя метод мысленных сечений отбросим верхнюю часть и заменим её действие н апряжениями p_. для равновесия p_ должны уравновешивать силу F и быть направлены параллельно оси стержня. В данном случае они не перпендикулярны площадке, по которой они действуют. Предположив, что на достаточном удалении от мест приложения внешних сил F напряжения p_ распределены по площади наклонного сечения равномерно, определим:

.

Но так как , то ,

где - нормальное напряжение в сечении А-А, перпендикулярном продольной оси стержня.

Разложим напряжение p_ на две составляющие: в плоскости А₁-А₁ и перпендикулярно к ней (рис. 15). Таким образом, произведём замену напряжения p_ двумя взаимно перпендикулярными напряжениями: нормальным напряжением _ и касательным _. Величина этих напряжений зависит от угла наклона сечения к продольной оси стержня:

,	(3.1)
	(3.2)

Из формул (3.1) и (3.2) следует, что наибольшие нормальные напряжения возникают по площадкам, перпендикулярным продольной оси стержня, а наибольшие касательные напряжения действуют по площадкам, составляющим угол 45^о с направлением продольной оси стержня, и равны половине наибольших нормальных напряжений.

	(3.3)
, при  = 45.

При любом  мы всегда будем иметь дело с двумя видами напряжений, действующих в каждой точке проведенного среза: с нормальными и касательными напряжениями. Наличие двух видов напряжений приводит к двум видам деформаций: удлинение и сдвиг. В практике целый ряд деталей конструкции работает на сдвиг, вследствие чего основное значение приобретает проверка их прочности по касательным напряжениям.

П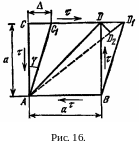 ри сдвиге из внутренних факторов Q_y0 или Q_z 0 остальные равны нулю.

Нормальные напряжения вызывают линейные деформации (удлинения и укорочения) элементов деформируемого тела. Касательные напряжения вызывают угловые деформации – сдвиги. Сдвиг характеризуется искажением прямого угла между двумя взаимно перпендикулярными волокнами, взятыми в деформируемом теле.

Рассмотрим плоский элемент в виде квадрата ABCD со стороной a, претерпевающий угловые деформации (рис.16). Абсолютный сдвиг элементарного отрезка CD относительно отрезка AB будет СС₁=.

Относительным сдвигом называется отношение . Так как деформации очень малы и практически не меняют первоначальных размеров тела, то можно записать:

,

(3.4)

где  - угол сдвига.

Закон Гука при сдвиге по аналогии с законом Гука при растяжении или сжатии можно записать:

,

(3.5)

где G – модуль упругости второго рода (модуль упругости при сдвиге).

Произведение GS – называют жесткостью тела при сдвиге.

Выражение (3.5) можно записать в иной форме:

.

Учитывая, что , а , получим:

(3.6)

Связь между упругими константами для материала (модулями упругости первого и второго рода) выражается формулой:

(3.7)

При деформации сдвига разрушение детали называется срезом. Условие прочности при сдвиге выражается формулой:

.

(3.8)