Деформация балки при изгибе

При действии внешних сил, расположенных в одной из главных плоскостей инерции балки, наблюдается искривление и оси той же плоскости.

Перемещение точки О, центра тяжести сечения в положение О₁, по направлению, перпендикулярному к оси балки, называется прогибом балки y в этом сечении. Угол , на который каждое сечение поворачивается по отношению к своему первоначальному положению, называется углом поворота.

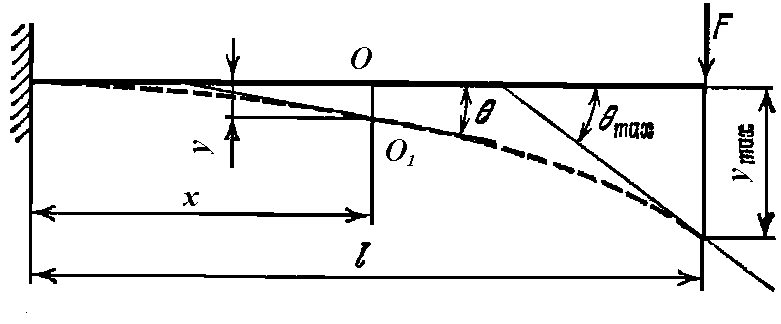
Рис. 36.

деформацию балки характеризует её упругая линия - нейтральная ось, искривленная при изгибе. для каждого сечения его прогиб y и угол поворота  будут функциями по x – расстояния сечения от начала координат.

Уравнение у=f(x) – уравнение кривой, по которой изогнётся ось балки под нагрузкой.

Тангенс угла  определяется так:

.

Учитывая, что на практике прогибы балок обычно малы по сравнению с длиной пролёта, то и  очень малы, обычно  1, тогда можно записать:

.

Для того, чтобы получить y как функцию от х, необходимо устанавливать зависимость деформации балки от внешних сил, изгибающих её, от размеров и физико-механических свойств материала.

Используем зависимость, полученную для случая чистого изгиба, пренебрегая влиянием поперечной силы:

,

где  радиус кривизны участка изогнутой оси балки между двумя смежными сечениями.

Для получения уравнения изогнутой оси балки используем математическую зависимость между радиусом кривизны оси и координатами её точек x и y:

.

(6.3)

Пренебрегая бесконечно малой величиной , получим приближенное дифференциальное уравнение изогнутой оси балки:

.

(6.4)

Тогда, после интегрирования, получим уравнение углов поворота:

,

(6.5)

интегрируя второй раз, получим уравнение прогибов:

,

(6.6)

где C и D постоянные интегрирования.

Учитывая, что при многих участках нагружения может быть несколько внешних сосредоточенных изгибающих моментов М, несколько внешних сосредоточенных сил F, а также распределенная нагрузка q может быть задана на нескольких участках, то уравнения углов поворота и прогибов можно записать в более общем виде:

,	(6.7)
,	(6.8)

где x_M, x_F, x_q – координаты точек приложения нагрузок или начало распределённой нагрузки, если (x-x_i)<0, то такие слагаемые отбрасываются:

- угол поворота сечения в начале координат,

- прогиб сечения в начале координат.

Такой метод составления уравнений перемещений называется методом начальных параметров, а сами уравнения этого метода называют универсальными уравнениями деформации балки с начальными параметрами.

При выводе уравнений принимается:

1. все реакции представляются как внешние силы;

2. начало координат общее для всех участков и связано с началом балки;

3. правило знаков для слагаемых определяется правилом знаков для изгибающего момента;

4. распределённая нагрузка распределяется до конца балки;

5. для продления равномерно-распределённой нагрузки на участке, где её нет, прикладывается равная по модулю и обратная по знаку нагрузка.