Относительное удлинение отрезка аа1:

.

Тогда в соответствии с законом Гука:

,

(5.4)

следовательно:

,

откуда , но - статический момент площади сечения относительно нейтральной оси. Статический момент площади равен нулю относительно оси, проходящей через центр тяжести сечения, тогда нейтральный слой совпадает с центральной плоскостью и проходит через центры тяжести всех поперечных сечений.

В соответствии с уравнением (5.2):

.

Выражение - осевой момент инерции, тогда:

или

(5.5)

Произведение Ej_y – называется жесткостью балки при изгибе. Чем это произведение больше, тем меньше искривится балка при действии данного изгибающего момента. Жесткость балки при изгибе зависит от материала, геометрических размеров и формы поперечного сечения.

С учетом уравнения (5.5) получим условие прочности по нормальным напряжениям:

,

(5.6)

где - осевой момент сопротивления сечения.

Потенциальная энергия деформации

Энергия накопленная в элементе бруса равна работе изгибающего момента М_y на взаимном угловом перемещении d двух сечений:

.

Учитывая, что , получим:

,

(5.7)

где l - длина участка чистого изгиба.

Лекция 6 Касательные напряжения при изгибе

При поперечном изгибе от действия внешних нагрузок в сечениях, перпендикулярных оси балки, возникают касательные напряжения. Рассмотрим балку прямоугольного поперечного сечения на двух опорах (рис. 33 a). В сечении m-m, удаленном от начала балки на расстоянии x, будет действовать внутренний изгибающий момент , а в сечении n-n - момент . Кроме того, по сечениям m-m и n-n действует внутренняя поперечная сила .

Относительно касательных напряжений  в этих сечениях д. И. Журавский сделал следующие предложения:

1. Направление всех касательных напряжений в сечении параллельно поперечной силе Q, которая является их равнодействующей.

2. Касательные напряжения, действующие по площадкам, расположенным на одном и том же расстоянии от нейтральной оси, равны между собой.

По левой грани бруска, ограниченного сечениями m-m и n-n (рис. 34), от действия внешнего момента возникают нормальные напряжения по правой .

П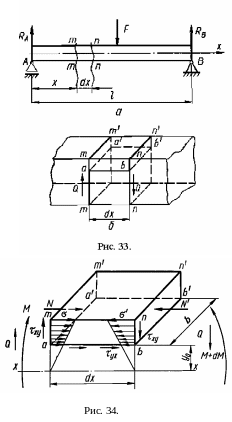 о боковым поверхностям действуют касательные напряжения _xy. По нижнему основанию бруска будут действовать касательные напряжения _yx, существование которых обусловлено законом парности касательных напряжений и подтверждено опытом. Наблюдением установлено, что концы составной балки при изгибе образуют ступеньки (рис. 35 а), поскольку оба бруса, составляющие балку, ничем не скреплены. У сплошной балки таких ступеней быть не может. Следовательно, по нейтральной поверхности должны существовать внутренние касательные напряжения, препятствующие разрушению балки по нейтральному слою (рис. 35 б).

Запишем условие равновесия выделенного бруска:

,

(6.1)

г де N и N - равнодействующие нормальных сил упругости, действующих по левой и правой граням, соответственно; b - ширина бруска.

Как известно и , тогда подставляя значения N и N в уравнение (6.1), получим:

,

откуда:

.

После преобразования получим:

, или ,

Учитывая, что , а , окончательно получим:

.

(6.2)

Формула (5.9) носит название формулы Журавского и справедлива для балок с поперечным сечением любой формы.