Індивідуальне завдання 4 Обробка експериментальних даних. Вибір апроксимуючої функції. Визначення параметрів цієї функції методом найменших квадратів.

Мета завдання - вивчення методики апроксимації експериментальних даних з використанням методу якнайменших квадратів.

Порядок виконання завдання

1. Відновити функціональну залежність по математичній моделі, що є багаточленом першого ступеня : (x) = a₀ + a₁x. По величині коефіцієнта кореляції зробити висновок про доцільність використовування даної моделі.

2. Відновити функціональну залежність по математичній моделі, що є багаточленом другого ступеня : (x) = a₀ + a₁x + а₂х₂ Результат представити графічно. Провести аналіз одержаного результату.

3. Оформити звіт і представити його до захисту.

Таблиця. 4.1.

Варіанти індивідуального завдання 4

____

Значення x_i=i*0.1 i=1,20 однакові для всіх варіантів

	Значення yi=y(xi)
i	варіант 1	варіант 2	варіант 3	варіант 4	варіант 5	варіант 6
1	5.998	6.031	5.348	6.456	5.567	6.323
2	5.980	6.041	5.156	6.198	5.198	6.001
3	5.970	6.067	5.096	6.003	5.001	5.897
4	5.851	6.191	5.001	5.936	4.876	5.576
5	5.769	6.257	4.986	5.741	4.598	5.308
6	5.672	6.378	4.761	5.598	4.373	5.173
7	5.358	6.645	4.598	5.373	4.401	4.908
8	5.400	7.015	4.372	5.198	4.115	4.915
9	5.312	7.153	4.258	5.009	3.896	4.709
10	5.391	7.256	4.198	5.109	3.907	4.517
11	5.199	7.371	4.072	4.981	3.568	4.506
12	5.095	7.598	3.961	4.798	3.375	4.498
13	5.076	7.643	3.752	3.576	3.178	4.371
14	5.036	7.786	3.534	2.498	3.236	4.182
15	5.029	7.815	3.296	2.056	2.908	3.954
16	5.015	7.867	3.197	1.978	2.506	3.503
17	5.021	8.011	3.081	1.753	2.307	3.478
18	5.019	8.153	2.990	1.538	2.296	3.501
19	5.024	8.296	2.576	1.296	2.184	3.400
20	5.053	8.361	2.387	1.178	2.006	3.382
	Значення yi=y(xi)
i	варіант 7	варіант 8	варіант 9	варіант 10	варіант 11	варіант 12
1	3.88	15.86	1.38	-1.77	-2.45	10.56
2	3.71	11.56	2.35	-1.38	-2.98	9.48
3	3.75	10.88	3.48	-1.11	-3.07	8.31
4	3.69	10.36	4.57	-1.09	-4.31	7.98
5	3.58	9.31	5.86	-0.91	-4.91	6.54
6	3.49	9.02	6.47	-0.76	-5.17	5.38
7	3.41	8.57	7.88	-0.58	-5.41	4.96
8	3.37	8.36	8.36	-0.35	-5.84	3.56
9	3.21	8.11	9.15	-0.29	-6.01	2.93
10	3.16	7.15	10.06	-0.11	-6.24	1.48
11	3.09	6.97	11.17	-0.08	-6.45	0.96
12	2.98	6.41	12.48	-0.01	-6.76	1.94
13	2.74	7.13	13.56	0.37	-6.92	2.56
14	2.56	7.58	14.17	0.60	-7.13	3.46
15	2.48	8.11	15.41	0.78	-7.47	4.83
16	2.36	8.96	16.07	1.13	-7.59	5.67
17	2.25	9.15	17.31	1.58	-7.91	6.78
18	2.33	9.98	18.15	2.01	-8.18	7.36
19	2.21	10.57	19.2	2.38	-8.46	8.51
20	2.19	11.71	20.11	2.74	-8.70	9.96
	Значення yi=y(xi)
i	варіант 13	варіант 14	варіант 15	варіант 16	варіант 17	варіант 18
1	20.48	3.88	-10.48	-0.01	-0.15	0.30
2	18.38	3.96	-9.93	-0.09	-0.38	0.50
3	17.15	4.01	-9.56	-0.17	-0.57	0.71
4	16.96	4.48	-9.13	-0.56	-0.91	0.92
5	15.37	4.91	-9.01	-0.78	-1.13	0.99
6	14.78	5.01	-8.84	-0.91	-1.56	1.01
7	13.11	5.36	-8.57	-1.10	-1.98	1.21
8	12.71	5.64	-8.32	-1.38	-2.06	1.43
9	11.56	5.97	-8.04	-1.43	-2.41	1.64
10	10.92	6.04	-7.78	-1.64	-2.87	1.82
11	9.01	6.43	-7.35	-1.87	-3.11	2.01
12	8.73	6.79	-7.19	-1.95	-3.45	2.24
13	7.64	7.01	-7.01	-2.01	-3.96	2.48
14	8.36	7.32	-6.48	-2.23	-4.17	2.56
15	9.56	7.57	-7.27	-2.48	-4.38	2.76
16	10.11	7.64	-8.54	-2.53	-4.67	3.01
17	11.37	7.98	-8.96	-2.64	-4.99	3.27
18	12.48	8.15	-9.13	-2.78	-5.06	3.49
19	13.56	8.49	-9.58	-2.83	-5.17	3.99
20	14.95	8.76	-10.02	-2.91	-5.38	4.07

	Значення yi=y(xi)
i	варіант 19	варіант 20	варіант 21	варіант 22	варіант 23	варіант 24
1	-5.06	2.43	1.56	-10.37	2.14	0.96
2	-4.98	2.94	0.99	-9.58	2.38	1.17
3	4.51	3.48	0.41	-8.36	2.54	1.38
4	-4.17	3.87	0.09	-7.14	2.79	1.53
5	-3.91	4.56	-0.99	-6.93	2.96	1.74
6	-3.63	4.99	-1.15	-5.17	3.11	1.91
7	-3.22	5.43	-1.76	-4.81	3.38	2.04
8	-3.09	5.87	-2.13	-3.76	3.42	2.29
9	-2.87	6.28	-2.98	-1.15	3.99	2.78
10	-2.54	6.79	-2.98	-1.15	3.99	2.78
11	-2.91	7.11	-3.14	-0.95	4.17	2.44
12	-3.07	7.38	-3.36	0.17	4.31	2.23
13	-3.38	7.69	-3.59	1.36	4.59	2.11
14	-3.74	8.01	-3.84	0.98	4.74	2.02
15	-3.96	8.37	-4.02	-0.38	4.93	1.95
16	-4.17	8.74	-4.29	-1.13	5.08	1.71
17	-4.64	9.12	-4.35	-2.48	5.29	1.59
18	4.91	9.49	-4.46	-3.01	5.54	1.32
19	-5.07	9.91	-4.98	-3.76	5.78	1.14
20	-5.38	10.13	-5.06	-4.11	6.01	0.86
	Значення yi=y(xi)
i	варіант 25	варіант 26	варіант 27	варіант 28	варіант 29	варіант 30
1	-2.09	-2.12	16.01	-1.77	-2.45	-1.61
2	-2.15	-1.96	15.76	-1.69	-2.57	-1.37
3	-2.37	-1.74	15.01	-1.58	-2.61	-1.29
4	-2.54	-1.69	14.58	-1.46	-2.78	-1.18
5	-2.96	-1.57	13.97	-1.37	-2.93	-1.05
6	-3.01	-1.46	13.41	-1.29	-3.01	-0.96
7	-3.38	-1.33	12.84	-1.17	-3.37	-0.56
8	-3.61	-1.29	12.37	-1.08	-3.49	0.26
9	-3.99	-1.17	11.91	-0.94	-3.54	0.05
10	-4.21	-1.10	11.05	-0.56	-3.71	0.27
11	-4.57	-1.05	10.82	-0.18	-3.98	0.70
12	-4.86	-0.96	10.54	-0.03	-4.05	1.15
13	-5.11	-0.78	11.15	0.11	-4.27	1.39
14	-5.38	-0.64	11.99	0.58	-4.58	1.98
15	-5.67	-0.59	12.54	0.94	-4.96	2.47
16	-5.98	-0.41	13.13	1.15	-5.07	2.89
17	-6.17	-0.32	14.01	1.37	-5.38	3.34
18	-6.41	-0.29	14.97	1.54	-5.64	3.57
19	-6.68	-0.15	15.17	1.98	-5.99	3.91
20	-6.84	-0.05	15.98	2.06	-6.07	4.21

Короткі відомості з теорії і основні алгоритми

Нехай потрібно дослідити залежність у(x). Для цього проведемо N дослідів в крапках x₁,x₂....x_n, в яких зареєструємо значення відгуку y₁,y₂....y_n. Сукупність значень:

х₁,x₂....x_n

y₁,y₂....y_n називається експериментом

де n - число експериментальних даних.

Задача полягає у відновленні функціональної залежності (x)по результатам експерименту.

В даний час існує два основні методи апроксимації експериментальних даних, заданих у вигляді таблиці.

Перший метод вимагає, щоб апроксимуюча крива проходила через всі крапки, задані таблицею.

Це задача інтерполяції.

- інтерполяційний багаточлен Лагранжа

Недолік методу - точність апроксимації гарантується лише в невеликому інтервалі за умови, що значення функції у вузлах задано з великою точністю. (рис 15)

Рис.15

Якщо погрішності вимірювання (x₁) значні і, крім того, необхідно мати єдину наближену формулу у (x),(рис 15 ) придатну для всієї області визначення аргументу х, то в цьому випадку потрібно використовувати метод найменших квадратів.

Цей метод дозволяє апроксимувати дані такою функцією, яка справедлива у всьому діапазоні табличних даних, і одержати результат з однаковою точністю у всьому діапазоні вимірювань.

Причому крива не обов'язково повинна проходити через всі крапки, але її необхідно провести так, щоб відхилення кривої від табличних даних були мінімальними. (рис 16)

За звичай мінімізують суму квадратів відхилень (SR) між значеннями функції, визначуваними вибраною кривою і табличними значеннями, тобто

___

y_i^Т = ( x_i, a₀, a₁ .... a_m ) і y_i, де i = I,N, тому такий метод називається методом найменших квадратів.

тоді результати експерименту можна представити у вигляді

Рис.16

у = ( x_i, a₀, a₁ .... a_m ) + _i

Часто (x) вибирають у вигляді багаточлена ступеня M<N :

( x_i, a₀, a₁ .... a_m ) = a₀ + a₁x + а₂х² + ...... + a_mx^m =

де a₀, a₁ .... a_m - постійні, але наперед невідомі параметри, які підлягають визначенню.

Для їх знаходження проводиться ряд вимірювань :

___

(x_i, y_i), i = 1,N

Якби x_i, y_i були визначені абсолютно точно, то для знаходження (m+1) параметра a_j, j=0,m було б достатньо виконати (m+1) вимірювання, проте x_i, y_i визначаються з деякою погрішністю, тому для знаходження a_j проводиться більше число вимірювань.

Визначення 1.

y_i = ( x_i, a₀, a₁ .... a_m ) + _i називається системою умовних рівнянь.

Ця система буде несумісною, тобто немає такої комбінації a₀, a₁..a_m щоб задовольнялися одночасно всі рівняння, тому слід шукати якнайкраще рішення.

Задача методу найменших квадратів (МНК) якраз і полягає в тому, щоб знайти такі значення параметра a_j, при яких сума квадратів відхилень знайденого багаточлена від заданих значень функції була мінімальною:

B точці мінімуму функції SR її похідні (по всіх параметрах a_j дорівнює нулю).

Визначення 2.

система нормальних (m+1) рівнянь з(m+1) невідомим.

Ця система розв'язується методом Гауса

Правило складання системи нормальних рівнянь:

Кожне j-е нормальне рівняння виходить шляхом множення кожного умовного рівняння на множник, що стоїть перед a_j, та подальшого складання одержаних рівнянь.

Лінійна регресія

За математичну модель обирається лінійна залежність:

Систему умовних рівнянь можна записати таким чином:

___

y_i = a₀ + a₁x_i + _i i = 1,N

Знайдемо параметри a₀ та a₁ методом найменших квадратів. Для цього мінімізуємо функцію

Система нормальних управлінь j =

Зауваження:

Математична модель справедлива для тієї області, для якої одержана, тобто на інтервалі [x₁,x_n].

Згідно правилу одержимо:

система двох рівнянь з двома невідомими (а₀,а₁)

Введемо позначення

_ _

тоді з першого рівняння a₀ = у - a₁x

Підставимо а0 в друге рівняння, одержимо:

|/N

звідки

або

- дисперсія, що виражає точність наглядів

- коефіцієнт кореляції, що характеризує ступінь залежності

між x і у |r_xy|1

При | r |1 залежність між x і у лінійна, причому при 0<r<1 експериментальні дані розташовано, в основному, в 1 і 3 квадрантах (рис 17 а), а при -1 < r < 0 - в 2 та 4 (рис 17 в).

Якщо | r |0, то або не існує залежності між x і у; або залежність не лінійна, а більш високого порядку (рис 17 с)

Рис. 17

Квадратична апроксимація

За математичну модель обираємо багаточлен другого ступеня

(x, a₀, a₁, a₂) = a₀ + a₁x + a₂x²

де a₀, a₁, a₂ - параметри підлягаючі визначенню методом МНК

З системи умовних рівнянь

yi = a₀ + a₁x_i + a₂x_i² + _i

Отримуємо систему нормальних рівнянь вигляду:

Введемо позначення:

А(3,3) - матриця коефіцієнтів; В(3) - вектор вільних членів

N - число експериментальних даних;

M - число невідомих

Матриця А симетрична щодо головної діагоналі.

Зауваження. Вектор В при вході в підпрограму "GAUSS"- вектор вільних членів, при виході - вектор невідомих, тобто

B(1)=a₀ B(2)=a₁ B(3)=a₂

Блок-схема алгоритму на рис. 18 і 19.

Рис. 18

Приклад 1. Відновлення функціональної залежності по математичній моделі, що є багаточленом першого ступеня : (x) = a₀ + a₁x за допомогою пакету MathCAD.

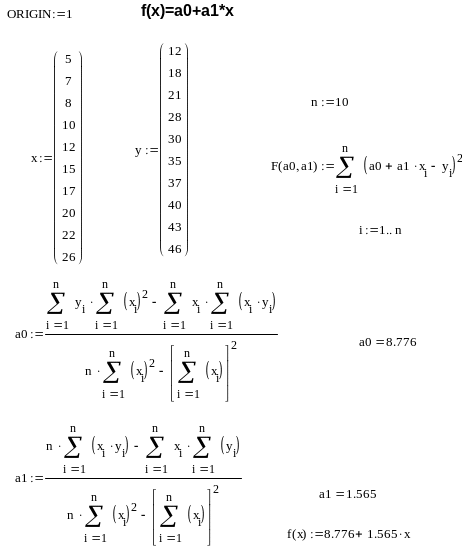
Індивідуальне завдання 5

Чисельні методи рішення задачі Коші для звичайних диференціальних рівнянь

Мета завдання - закріплення теоретичного матеріалу, складання алгоритмів і програм для вирішення систем диференціальних рівнянь першого порядку, що задовольняють початковим умовам.

Порядок виконання завдання

1. Скласти головну програму, що містить звернення до підпрограм EYLER, RGK.

2. Скласти підпрограму обчислення правих частин рівнянь системи.

3. Провести обчислення на ЕОМ.

4. Провести аналіз одержаних результатів.

5. Оформити звіт і представити його до захисту.

Таблиця 5.1.

Варіанти індивідуального завдання 5

а)

Номер варіанту	f ( x; y1, y2)	а	y20
1 2 3 4 5 6	-a0.8x	0.01 0.02 0.03 0.05 0.07 0.09	0.05 1/3 0.25 0.2 1/6 1/9
7 8 9 10	-axy2-y1	0.01 0.02 0.03 0.04	0.5 0.33 0.25 0.2
11 12 13 14	-ay1e-x	0.01 0.02 0.05 0.06	0.5 1/3 0.25 0.2
15 16 17	-0.04e-1..2x	- - -	0.2 0.3 0.4
18	-0.04e0.8	-	0.2
19 20 21 22	-axy2-x2y1		0.2 1/6 1/7 0.125

б) привести до системи диференціальних рівнянь шляхом введення додаткових змінних

уу(1), y’ у (2), у” у(3) і т.д.

Таблиця 5.2.

Номер варіанту	Диференціальне рівняння	Інтервал [а;b]	x0	y0	y0’	Крок h
23	y”=3y’-2y+2x-3	0; 0.3	0	1	0	0.1
24	y”+4y’+4y=0	0; 0.5	0	1	-1	0.05
25	y”+yy’-6y=2x2-x	0; 0.6	0	-1	1	0.1
26	y”+2y’+2y=2e-xcosx	0; 1	0	1	0	0.1
27	(1+x2)y”+(y’)2+1=0	1; 2	1	1	-1	0.1
28	y”+4y=sinx+sin2x	0; 1	0	1	-0.5	0.1
29	у(3)=y”-y’+1	0; 2	0	1	0	0.4

в)

Таблиця 5.3.

Номер варіанту	f1 ( x; y1; y2 )	f2 ( x; y1; y2)	Інтервал [а;b]	x0	y10	y20	Крок h
30	y1+y2+x	-4y1+3y2+2x	0; 0.3	0	1	0	0.05

Короткі відомості з теорії і основні алгоритми

Визначення 1. Диференціальне рівняння - рівняння, що містить невідому функцію одного або декількох змінних, незалежні змінні і похідні невідомої функції по незалежним змінним.

Приклади:

- невідома функція (1)

- невідома функція (2)

невідома функція (3)

Визначення 2. Звичайним диференціальним рівнянням порядку r називається рівняння (щодо невідомої функції у одного незалежного х ) вигляду :

F (x, у(x), y'(x) ... у^(r)(x)) = 0 (4)

де r - порядок щонайвищої похідної, входить в рівняння.

Визначення 3. Якщо рівняння лінійне по у, y' .. у^{( r} ), то воно називається лінійним .

Визначення 4. Під диференціальним рівнянням в явній формі розуміють диференціальне рівняння, яке вирішено щодо старшої похідної:

у^(r) (x)= f (x, у(x), y'(x) ... у^(r-1)(x)) ⁽5)

Визначення 5. Рівняння (4) називається рівнянням в неявній формі.

Вирішити диференціальне рівняння - це значить знайти всі невідомі функції, обертаючі рівняння в тотожність. В загальному випадку невідомі функції визначаються диференціальним рівнянням неоднозначно (якщо рішення взагалі існує), тому на шукані функції часто накладаються додаткові умови.

Під інтеграцією рівняння (4) розуміють знаходження функції у(x), що задовольняє цьому рівнянню. При цьому у(x) називається рішенням диференціального рівняння.

Загальне рішення звичайного диференціального рівняння порядку r має вигляд

у = у ( x; С₁ ... C_r)

де C₁...C_r - довільні постійні.

При будь-якому наборі конкретних постійних виходять приватні рішення.

Задача Коші (задача з початковими умовами) є задача про знаходження приватного рішення яке задовольняє r початковим умовам

у(x₀)=y_0, y'(x₀)=y₀', ... у^(r-1)(x₀)=y₀^(r-1)

Якщо відоме загальне рішення, то для вирішення задачі Коші постійні знаходять з рівнянь

у(x; C₁ ... C_r )= y₀

Визначення 6. Графічне зображення приватного рішення називають інтегральною кривою

Загальне рішення диференціального рівняння r-го порядку визначає r-параметричне сімейство інтегральних кривих. Зворотно, кожне r-параметричне сімейство визначає (за деяких додаткових умов) диференціальне рівняння r-го порядку, яке виходить шляхом виключення постійних C₁...C_r з рівнянь

___

у⁽ⁱ⁾ (x)= у⁽ⁱ⁾ (x; C₁ ... C_r ) ( i = 0, r )

Таким чином диференціальне рівняння описує сімейство кривих.

Приклад:

Сімейство всіх кіл на площині ( x - C₁ )² + ( y-C₂ )² = C₃² містить три параметри. Триразове диференціювання приводить до рівнянь

x - C₁ + ( у - C₂ ) y' = 0

1 + ( у - C₂ ) y'' + ( y' )² = 0

( у - C₂ ) y'''+ 3y'y'' = 0

Виключаючи С₂ з двох останніх рівнянь, отримуємо

y'''( 1 + (y')² ) - 3y' ( y'') 2 = 0

Диференціальне рівняння в явній формі має вигляд:

y'= f(x,y)

Якщо через точку М(x,y) проходить графік рішення y=y(x) рівняння y'= f(x,y), то нахил φ дотичної до графіка в точці М(x,y) визначається безпосередньо з рівняння

tg φ = y'(x)= f(x,y)

Таким чином диференціальне рівняння в кожній крапці даної області задає напрям дотичної до кривої рішення. Через кожну крапку проходить єдина інтегральна крива.

Будь-яке диференціальне рівняння n - порядку, яке можна дозволити щодо старшої похідної, легко зводиться з n рівнянь першого порядку шляхом введення нових змінних.

у⁽ⁿ⁾= f( x; y', y'' ..., у^(n-1))

y₁ = у

y₂ = y'

y₃ = y'' (6)

. . .

y_n = у^(n-1)

тоді

(7)

Чисельне рішення задачі Коші полягає в побудові таблиці наближених значень y₁, y_{2 ...,} y_m рішення рівняння в крапках (вузлах) сітки:

x_i = x₀ + ih, i = 1, 2 ..., M ; x₀ = а, x_m = b ; h - крок інтеграції