
- •Вимірювання фізичних величин Теоретичні відомості
- •Похибки прямих вимірювань
- •Похибки непрямих вимірювань
- •Лабораторна робота № 1 вивчення руху тіла під дією сили тяжіння
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •5. Під яким кутом до горизонту треба направляти струмінь води, щоб висота її підйому дорівнювала дальності польоту? Лабораторна робота № 2 вивчення руху тіла, кинутого горизонтально
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 3 визначення прискорення тіла при рівноприскореному русі
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 4 визначення прискорення вільного падіння методом математичного маятника
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 5 вивчення коливань пружинного маятника
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •12. Запишіть диференціальне рівняння руху пружинного осцилятора.
- •13. Опишіть перетворення енергії при гармонічних коливаннях вантажу на пружині. Лабораторна робота № 6 визначення маси тіла методом гідростатичного зважування
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Контрольні запитання
- •Лабораторна робота № 8 вимірювання коефіцієнта тертя ковзання
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 9 вивчення умови рівноваги важеля
- •Теоретичні відомості
- •Порядок виконання роботи
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 11 вимірювання атмосферного тиску
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 12 визначення коефіцієнта поверхневого натягу рідини методом відриву петлі
- •Теоретичні відомості
- •Опис приладу
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 13 визначення коефіцієнта внутрішнього тертя рідини методом стокса
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Вимірювання відносної вологості повітря за допомогою психрометра і гігрометра
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 15 вивчення теплового балансу при змішуванні води різної температури
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Рекомендована література
Похибки непрямих вимірювань
При
непрямих вимірюваннях значення певної
фізичної величини
![]() обчислюють за відомою формулою
обчислюють за відомою формулою
![]() .
.
При
цьому
![]() – незалежні величини, значення яких
визначають безпосередньо у досліді
(або шляхом розрахунків) і подають у
вигляді:
– незалежні величини, значення яких
визначають безпосередньо у досліді
(або шляхом розрахунків) і подають у
вигляді:
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
де
![]() – межі абсолютних похибок величин
– межі абсолютних похибок величин
![]() відповідно.
відповідно.
Найкраще
значення величини
при непрямому її вимірюванні визначається
через середні значення величин
![]() :
:
![]() .
.
Загальні
правила обчислення похибок при непрямих
вимірюваннях отримують за допомогою
диференціального числення. При цьому
вважається, що межі абсолютних похибок
![]() завжди
малі
порівняно із значеннями відповідних
вимірюваних величин. Розглянемо спочатку
найпростіші випадки.
завжди
малі
порівняно із значеннями відповідних
вимірюваних величин. Розглянемо спочатку
найпростіші випадки.
Якщо
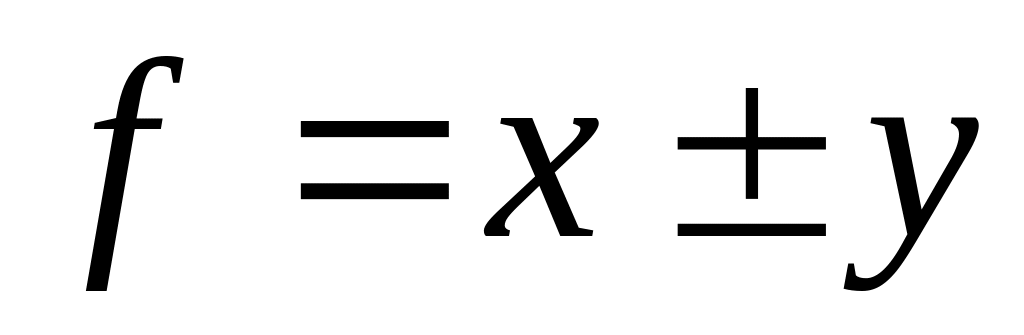 ,
то
,
то
 .
.
Дійсно, диференціал функції запишеться у вигляді
![]() .
.
За умови,
що межі абсолютних похибок величин
та
![]() є досить малими порівняно із значеннями
цих величин, можна наближено замінити
диференціали в останній рівності на
межі відповідних абсолютних похибок:
є досить малими порівняно із значеннями
цих величин, можна наближено замінити
диференціали в останній рівності на
межі відповідних абсолютних похибок:
![]() ,
,
![]() ,
,
![]() .
.
При
цьому для оцінки межі абсолютної похибки
![]() знак “–”
треба опустити. Отже,
.
Межа відносної похибки
знак “–”
треба опустити. Отже,
.
Межа відносної похибки
![]() .
.
Якщо величина визначається добутком двох інших величин та або їх відношенням:
![]() або
або
![]() ,
,
то
спочатку легше оцінити межу відносної
похибки
![]() ,
яка в цих випадках визначатиметься за
формулою:
,
яка в цих випадках визначатиметься за
формулою:
![]() . (17)
. (17)
Межу абсолютної похибки у цьому разі можна оцінити так:
![]() .
.
Для
обґрунтування формули (17) розглянемо,
наприклад, випадок
![]() .
Прологарифмуємо обидві частини цієї
рівності:
.
Прологарифмуємо обидві частини цієї
рівності:
![]() .
.
Знайдемо диференціали обох частин:
![]() .
.
Після наближеної заміни диференціалів в останньому рівнянні відповідними межами абсолютних похибок (за умови їх мализни), а також замінивши знак “мінус” на “плюс”, отримуємо
![]() ,
,
звідки
.
З формули
(17) випливає, що якщо
![]() ,
то
,
то
![]() ,
а для більш загального вигляду степеневої
функції
,
а для більш загального вигляду степеневої
функції
![]() (де
– сталий множник,
(де
– сталий множник,
![]() ),
),
![]() .
.
Розглянутий прийом можна легко узагальнити на досить поширену у навчальному фізичному практикумі функцію вигляду:
![]() .
.
Тоді
![]() .
.
Приклад.
Нехай вимірюється питомий опір матеріалу
провідника. Тоді
![]() та
.
Якщо провідник має циліндричну форму,
то
та
.
Якщо провідник має циліндричну форму,
то
![]() .
.
Межа відносної похибки
![]() .
.
При
цьому межу абсолютної похибки можна
знайти за формулою
![]() .
.
Загальний
випадок. Нехай
шукана величина
є функцією інших величин
![]() :
:
![]() .
.
Повний диференціал функції багатьох змінних
![]() .
.
Після наближеної заміни диференціалів в останній формулі кінцевими приростами – межами абсолютних похибок відповідних величин, та заміни частинних похідних їх абсолютними значеннями, отримаємо формулу для оцінки межи абсолютної похибки величини :
 ,
(18)
,
(18)
де
![]() – межі абсолютних похибок величин
відповідно
(
– додатні величини). У формулі (18) частинні
похідні обчислюються при найкращих
значеннях
– межі абсолютних похибок величин
відповідно
(
– додатні величини). У формулі (18) частинні
похідні обчислюються при найкращих
значеннях
![]()
Приклад.
У
досліді були виміряні відстань
![]() від точкового об’єкта до збиральної
лінзи
від точкового об’єкта до збиральної
лінзи
![]() та відстань
від зображення до лінзи
та відстань
від зображення до лінзи
![]() .
За цими даними знайти оптичну силу
лінзи.
.
За цими даними знайти оптичну силу
лінзи.
Оптичну силу лінзи знайдемо за формулою тонкої лінзи
![]() ,
,
![]() .
.
Межу
абсолютної похибки
![]() знайдемо, скориставшись формулою (18):
знайдемо, скориставшись формулою (18):
![]() ,
,
![]() .
.
Отже, згідно з правилами запису результату
![]() ,
,
![]() .
.
Як було показано на окремих прикладах, інколи легше спочатку оцінити межу відносної похибки . Для отримання загальної формули для прологарифмуємо функцію та знайдемо диференціали обох частин отриманого рівняння:
![]() .
.
Після наближеної заміни диференціалів в останньому рівнянні межами абсолютних похибок відповідних величин, та заміни частинних похідних їх абсолютними значеннями, отримаємо:
![]() .
.
Вище нами було показано, що середнє квадратичне відхилення суми взаємно незалежних випадкових величин дорівнює не сумі середніх квадратичних відхилень цих величин, а кореню квадратному із суми квадратів цих відхилень:
![]() .
.
Ця обставина дозволяє уточнити формули для оцінки похибок при непрямих вимірюваннях. Наведемо ці формули без доведення.
Нехай значення шуканої величини знаходиться шляхом додавання декількох інших величин:
![]() (19)
(19)
Найкраще значення величини (найбільш близьке до істинного) знаходять при цьому шляхом додавання найкращих значень величин за формулою (19).
Межа абсолютної похибки величини зв’язана з межами абсолютних похибок формулою
![]() .
.
Межі абсолютних похибок при цьому можуть бути отримані з досліду (якщо величини безпосередньо вимірюються) або знайдені шляхом обчислень (якщо самі отримані в результаті розрахунків).
Нехай шукана величина зв’язана з іншими величинами формулою:
![]() ,
(20)
,
(20)
де
![]() – будь-які числа, цілі або дробові,
додатні або від’ємні. Теорія ймовірності
показує, що найкраще значення
обчислюється за допомогою (20) через
найкращі значення
– будь-які числа, цілі або дробові,
додатні або від’ємні. Теорія ймовірності
показує, що найкраще значення
обчислюється за допомогою (20) через
найкращі значення
![]() ,
тобто
,
тобто
![]() .
.
При цьому межа відносної похибки знаходиться за формулою (21):
![]() .
.
Як і у першому випадку, величини знаходяться безпосередньо з досліду або шляхом розрахунків за допомогою інших величин, які вимірюються вже безпосередньо.
Загальний випадок. Нехай шукана величина є певною функцією інших величин так, що .
В цьому випадку межа абсолютної похибки дорівнюватиме
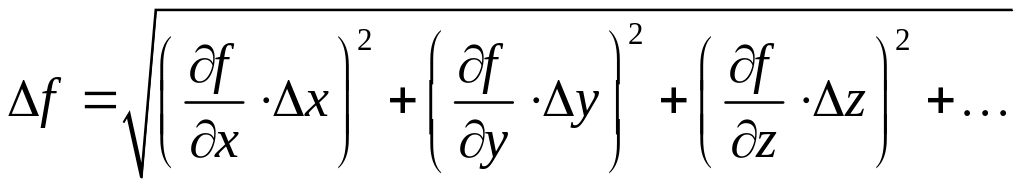 .
.
В останній формулі частинні похідні обчислюються при найкращих значеннях величин .
Зазначимо,
що розрахункова формула для визначення
величини
може містити, окрім величин
,
ще й сталі величини. Ними можуть бути
математичні константи:
![]() ;
фізичні константи: елементарний заряд,
прискорення вільного падіння, табличні
дані тощо. Бажано, щоб відносна похибка
значень цих величин була меншою за
відповідну похибку виміряних величин
;
фізичні константи: елементарний заряд,
прискорення вільного падіння, табличні
дані тощо. Бажано, щоб відносна похибка
значень цих величин була меншою за
відповідну похибку виміряних величин
Приклад.
Нехай
об’єм
![]() циліндра визначається за результатами
прямих вимірювань його діаметра
циліндра визначається за результатами
прямих вимірювань його діаметра
![]() та висоти
та висоти
![]() за допомогою формули
за допомогою формули
![]() .
.
У вираз
для
разом з вимірюваними величинами
і
входить число
![]() ,
яке ми звичайно округляємо до
,
яке ми звичайно округляємо до
![]() .
Тому перед тим як проводити обчислення,
необхідно з’ясувати, чи достатньо такої
точності, щоб похибка цієї константи
не впливала на точність визначення
об’єму. Розглядаючи
як число, задане з похибкою
.
Тому перед тим як проводити обчислення,
необхідно з’ясувати, чи достатньо такої
точності, щоб похибка цієї константи
не впливала на точність визначення
об’єму. Розглядаючи
як число, задане з похибкою
![]() ,
для межи відносної похибки згідно з
(21) отримуємо
,
для межи відносної похибки згідно з
(21) отримуємо
 .
.
Відносна
похибка завдання
,
тобто величина
![]() ,
повинна бути меншою за
,
повинна бути меншою за
![]() і
і
![]() .
При округленні
до
ми допускаємо абсолютну похибку
.
При округленні
до
ми допускаємо абсолютну похибку
![]() (більш точне значення
(більш точне значення
![]() ),
тому
),
тому
![]() .
Цією похибкою можна знехтувати порівняно
із
.
Цією похибкою можна знехтувати порівняно
із
![]() і
і
![]() .
.
Отже,
![]() .
.
Межа відносної похибки об’єму
 .
.
Кінцевий
результат:
![]() ,
,
![]() . Метод
меж. Для
обробки результатів при непрямих
вимірюваннях можна також застосовувати
метод
меж. Згідно
з цим методом наближене значення
вимірюваної величини знаходять як
півсуму нижньої
. Метод
меж. Для
обробки результатів при непрямих
вимірюваннях можна також застосовувати
метод
меж. Згідно
з цим методом наближене значення
вимірюваної величини знаходять як
півсуму нижньої
![]() і верхньої
і верхньої
![]() її меж:
її меж:
![]() ,
,
а абсолютну похибку оцінюють як піврізницю цих меж:
![]() .
.
Самі ж межі і визначають за допомогою розрахункової формули для величини . При цьому значення округляють з надлишком, а – з нестачею до однієї значущої цифри. Кінцевий результат записують у вигляді
![]() .
.
Приклад.
Для
вимірювання фокусної відстані збиральної
лінзи отримано такі результати: відстань
від лінзи до точкового об’єкта
![]() ;
відстань від лінзи до його зображення
;
відстань від лінзи до його зображення
![]() .
Знайдіть фокусну відстань
.
Знайдіть фокусну відстань
![]() лінзи із застосуванням методу меж.
лінзи із застосуванням методу меж.
Фокусну відстань лінзи знайдемо з формули тонкої лінзи
![]() ,
,
звідки
 .
.
Знайдемо верхні та нижні межі для та :
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Тепер знаходимо межі для фокусної відстані :
 ,
,
 .
.
Оцінимо абсолютну похибку
![]() .
.
Наближене значення фокусної відстані
![]()
Отже,
![]() .
.
