Частина 2. Приклади побудови математичних моделей

 

1. Біологічні моделі

 

 

1. Біологічні моделі

1.2. Популяційні моделі

1.2.2. Модель одновидової популяції з урахуванням насичення (логістична модель)

1.2.3. Логістична модель з урахуванням зовнішніх впливів

1.2.4. Модель двовидової популяції Лотки – Вольтерра

1.2.5. Модель багатовидової популяції

1.2.6. Узагальнення моделі багатовидової популяції. Побудова ієрархічного ланцюга

 

 

Перейдемо до побудови й дослідження конкретних математичних моделей із застосуванням викладеної вище теоретичної бази. На прикладах проілюструємо прийоми й методи математичного моделювання.

 

1. Біологічні моделі

Будь-яку кінетичну біологічну систему можна охарактеризувати як сукупність деяких параметрів, значення яких підтримуються незмінними протягом часу спостереження за системою, та змінних у часі. Параметрами є, наприклад, такі фізичні величини, як температура, вологість, електрична провідність мембрани, рН і т. д. Залежно від досліджуваних біосистем змінними вважаються: в екології – чисельність виду, у біофізиці – мембранний потенціал, у мікробіології – кількість мікроорганізмів, у біохімії – концентрація речовини тощо.

Припустимо, що в біосистемі є  різних компонент (напр., хімічних сполук), які з часом зазнають метаболічних перетворень. Це означає, що значення концентрації  кожної -ї сполуки ( ) змінюється з часом унаслідок її взаємодії з будь-якою іншою ( ) компонентою. Такого припущення достатньо для побудови загальної математичної моделі, яка є системою  диференціальних рівнянь першого порядку.

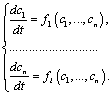                                                (2.1.1)

 

 

У системі (2.1.1), де   – швидкості зміни невідомих концентрацій (змінних), – деякі функції, які можуть залежати як від внутрішніх (напр., рН), так і від зовнішніх (напр., температура) параметрів біосистеми.

Знайти загальний розв'язок моделі (2.1.1) в аналітичному вигляді, як правило, вдається лише тоді, коли вона є лінійною. Однак процеси, які відбуваються в біологічних системах, як правило, є нелінійними; відповідно нелінійними є й математичні моделі цих процесів. Проте існують методи якісного аналізу диференціальних рівнянь, які дають можливість виявити важливі загальні властивості (закономірності) моделі (2.1.1), не знаходячи в явному вигляді невідомі функції .

Ці методи базуються на таких експериментальних фактах. По-перше, різні функціональні процеси в біосистемах суттєво відрізняються один від одного за часом проходження або характерними швидкостями. Так, наприклад, у біосистемі одночасно мають місце швидкі процеси ферментативного каталізу (час обороту ферменту становить с), фізіологічні процеси (час – хвилини) та процеси репродукції (від кількох хвилин і більше). По-друге, якщо окремі (проміжні) стадії загального процесу в біосистемі характеризуються часом  і найповільніша стадія має час  такий, що , то визначальною ланкою всього процесу є -та стадія, і загальний час проходження процесу практично збігається з . Отже, наявність такої часової ієрархії процесів у біосистемі дає можливість значно спростити вихідну модель, звівши її, по суті, до кінетичного опису поведінки найбільш повільної стадії.

Як видно з рівнянь (2.1.1), зміна стану системи описується деякою точкою  у -мірному просторі значень змінних . Простір з координатами  називається фазовим. Крива, яку описує в цьому просторі точка , називається фазовою траєкторією.

Однією з важливих властивостей відкритих систем (на відміну від ізольованих) є наявність у них стаціонарних станів. За означенням, у стаціонарному стані

.                          (2.1.2)

У результаті отримуємо систему алгебраїчних рівнянь для визначення стаціонарної (особливої) точки фазового простору :

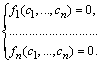                           (2.1.3)

 

 

 

Динамічні біосистеми, які описуються за допомогою звичайних диференціальних рівнянь типу (2.1.1), називаються точковими системами. Це означає, що в будь-якій точці такої системи значення шуканої величини (напр., концентрації речовини) зберігається з часом. Однак загальнішим є випадок, коли значення змінних є різними в різних точках простору. Наприклад, коли одночасно з реакцією, яка відбувається на деякій ділянці системи, реагенти дифундують, переходячи до іншої ділянки. Кінетичні рівняння, які враховують дифузійний зв’язок між окремими ділянками простору в біосистемі, мають вигляд

        (2.1.4)

де – коефіцієнт дифузії речовини , – просторова координата.

Система рівнянь (2.1.4) дає можливість пояснити деякі загальні принципи процесів самоорганізації в живих організмах.