4.3. Методика знаходження критеріїв подібності за відсутності математичного описання об’єкта

У загальному випадку методика знаходження критеріїв подібності на основі аналізу розмірностей і -теореми, коли математичне описання об’єкта невідоме, полягає в такому:

1. Установлюються всі  фізичних величин:

,

що визначають стан або поведінку об’єкта, який розглядається.

2. Установлюються розмірності всіх  визначальних величин у будь-якій системі одиниць виміру (як правило, у системі СІ).

3. Розмірності одних величин виражаються через розмірності інших:

.

У результаті встановлюється кількість  величин, які мають незалежні розмірності, і кількість критеріїв подібності .

4. На основі складених формул розмірностей і згідно із системою (1.4.17) знаходять критерії подібності .

Приклад. Розглядається явище піднімання рідини всередині капілярної трубки, яка занурена в рідину.

1. Висоту підйому рідини  визначають внутрішній радіус трубки , питома вага рідини  і поверхневий натяг  рідини.

Отже, визначальними фізичними величинами явища є . Їхня кількість .

2. Розмірності визначальних величин у системі СІ є такими:

.

3. Складаємо формули розмірностей:

.     (1.4.23)

Звідси основними визначальними фізичними величинами є  і , тому що вони мають незалежні розмірності. Залежними визначальними фізичними величинами є  і  – вони мають залежні розмірності.

4. На основі знайдених формул розмірностей (1.4.23) отримаємо два критерії подібності:

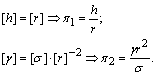
Таким чином, згідно з аналізом розмірностей і -теоремою залежність між  може бути зображеною у вигляді

.

Функція , однак, залишається невизначеною.

Конкретний вираз для критеріїв подібності

 

 

у рівнянні визначається тим, які з визначальних величин вибираються за такі, що мають незалежні розмірності. Оскільки це може бути зроблено по-різному, то форма критеріїв подібності може бути різною. Однак кожна з цих форм завжди може бути перетвореною на будь-яку іншу.

Приклад. Якщо в попередньому прикладі за величини з незалежними розмірностями вибрати не  і , а  і , то на основі формул розмірностей

отримаємо інші критерії подібності:

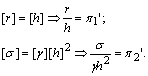
Однак

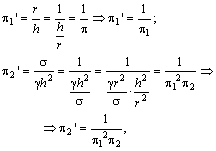
або

.

 

 

Успіх цього методу знаходження критеріїв подібності залежить від того, наскільки правильно встановлені величини, які визначають об’єкт дослідження. Якщо деякі величини пропущено або вони є зайвими, то тип і кількість критеріїв подібності буде встановлено невірно.

У складних випадках, коли кількість визначальних величин є великою, найпростіший – евристичний – спосіб складання формул розмірностей для величин із залежними розмірностями і знаходження за ними критеріїв подібності є незручним і може призвести до суттєвих помилок.

Найпоширеніший метод формального характеру – це метод, який потребує складання й розв’язання деякої системи лінійних алгебраїчних рівнянь. Цей метод вивчається у більш загальних курсах лекцій з математичного моделювання.

Найзручнішим для практичного застосування є метод вилучення розмірностей. Він полягає в поступовому вилученні із системи формул розмірностей визначальних величин

 

 

 

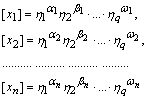
усіх символів розмірностей  основних визначальних величин з одночасним зменшенням кількості формул з  до . У міру зменшення кількості формул їх праві частини спрощуються, а в лівих частинах формуються все складніші степеневі комплекси з визначальних величин. Поява, унаслідок виключення чергового символу , рівності, що містить у правій частині одиницю, означає, що в лівій її частині сформовано безрозмірний степеневий комплекс – критерій подібності. Порядок виключення символів розмірностей  не має значення.

Приклад. Перехідний процес в електричному контурі, який складається з резистора, конденсатора й дроселя, при вмиканні синусоїдної напруги визначають сім величин: струм , амплітуда напруження , опір , ємність , індуктивність , час  і частота . Отже, . Випишемо формули розмірностей усіх семи визначальних величин у системі СІ:

 

 

 

 

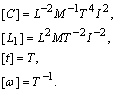
Виключимо з формул розмірностей символ  – розмірність часу . Для цього поставимо собі питання: на скільки треба помножити , щоб добуток у формулі розмірностей не містив символу розмірності часу ? Ураховуючи, що формула розмірності для  містить  у степені (-3), отримаємо, що  слід помножити на , тоді  не буде містити в правій частині символ  – розмірність часу . Отже, . Зробимо те саме з усіма іншими формулами розмірностей. Отримаємо

 

 

У результаті знаходимо перший критерій подібності .

Виключимо  з п’яти формул, що залишилися, – це символ розмірності струму :