5.6. Тригонометричні рівняння

Не існує єдиного методу побудови розв’язку тригонометричних рівнянь. Можна лише зазначити, що перетворення тригонометричних виразів має бути спрямовано на те, щоб рівняння набувало стандартного вигляду або «розпадалося» на кілька стандартних (простіших) рівнянь. Наведемо лише кілька методів побудови розв’язків тригонометричних рівнянь, тим паче що використання їх буде корисним у подальшому вивченні курсу вищої математики:

1. Введення додаткового аргументу за формулою

.

Оскільки то величини і можуть бути косинусом і синусом деякого кута . Якщо, наприклад, позначити , а , то отримаємо вищенаведену формулу.

2. Зведення рівняння до алгебраїчного після заміни тригонометричної функції.

3. Розкладання на множники.

Слід також запам’ятати розв’язки так званих найпростіших тригонометричних рівнянь:

, , , ;

, , , ;

, , , ;

, , , .

Окрім загальних формул розв’язків найпростіших тригонометричних рівнянь корисно знати формули для так званих «окремих випадків» розв’язків найпростіших тригонометричних рівнянь:

, , ; , , ;

, , ; , , ;

, , ; , , ;

, , .

Приклад 5.32. Розв’язати рівняння .

Розв’язання. Задано рівняння . Його розв’язок: , або .

Приклад 5.33. Розв’язати рівняння .

Розв’язання. Якщо поділити обидві частини на 2, то можна записати рівняння у вигляді , або , ; звідси , , .

Приклад 5.34. Розв’язати рівняння .

Розв’язання. Розкладемо ліву частину рівняння на множники, використовуючи формулу суми кубів:

Це рівняння рівносильне сукупності рівнянь

Перше з них розв’язків не має , а до другого застосуємо такі перетворення:

Таким чином,

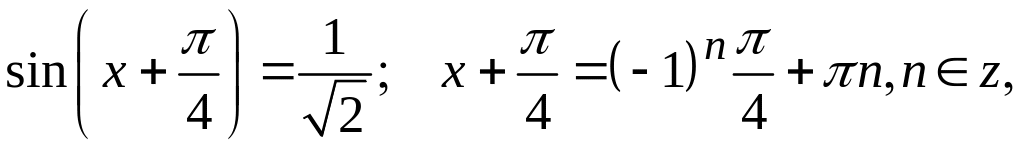
або

Приклад 5.35. Розв’язати рівняння

Розв’язання. До лівої частини рівняння застосуємо формулу різниці синусів, а далі отриманий вираз розкладемо на множники. Маємо:

Приклад 5.36. Розв’язати рівняння

Розв’язання. ОДЗ цього рівняння знаходиться з умови , тобто . Звільнившись від знаменника,отримаємо , , , . Остання множина при збігається з множиною , яка не входить в ОДЗ. Тому наведене рівняння розв’язків не має.

Приклад 5.37. Розв’язати рівняння

Розв’язання. Скористаємося основною тригонометричною тотожністю і перепишемо рівняння у вигляді

Покладемо і розв’яжемо квадратне рівняння: , де . Оскільки , то рівняння розв’язків не має. Розв’язком рівняння , а значить, і всього рівняння є множина

Приклад 5.38. Розв’язати рівняння

Розв’язання. Оскільки для будь-якого розв’язку цього рівняння , то поділимо це рівняння на . Отримаємо рівняння . Звідси

, або .

Приклад 5.39. Розв’язати рівняння

Розв’язання. Використовуючи формулу подвійного кута, перепишемо рівняння у вигляді а потім поділимо його на . Отримаємо Останнє рівняння є алгебраїчним рівнянням відносно , а саме Розв’язок цього рівняння такий: . Маємо:

Завдання для самостійної роботи

5.18. Розв’язати найпростіші тригонометричні рівняння:

а) ; b) ; c) ; d)

e) ; f) ; g) ; h) .

Розв’язки рівнянь зобразити на тригонометричному колі.

Розв’язати тригонометричні рівняння:

5.19. а) ; b) ; c) ;

d) ; e) ; f) .

5.20. 5.21. 5.22.

5.23. 5.24. 5.25.

5.26. 5.27. 5.28.

5.29. 5.30. 5.31.

5.32. 5.33.

5.34. 5.35.

5.36. 5.37.

5.38. 5.39. .