Дополнительные свойства систем управления

1. Точность.

Под точностью систем управления понимают предельно допустимые значения выходных параметров системы в стационарном состоянии , то есть после окончания переходного процесса.

Рассмотрим математическую форму критериев точности. Представим обобщённое динамическое уравнение системы в операторной форме

В стационарном состоянии (при р = 0) получим . Зададим условие точности , тогда , при этом возможны варианты:

а)

б) ,

то есть точность определяется как вариацией внешних воздействий на систему, так и возможными изменениями параметров самой системы.

2. Законы управления

Под законами управления подразумевают математическую форму изменения параметров системы (как внутренних, так и внешних) для достижения определённого конечного результата управления.

Различают линейные, нелинейные функциональные, нелинейные логические и нелинейные оптимизирующие законы управления.

Примеры:

а) - линейный закон

б) - нелинейный функциональный закон

в) - нелинейный логический закон

где а — параметр зоны нечувствительности

г) - нелинейный оптимизирующий закон.

Смысл перечисленных законов управления заключается в создании определённой структуры системы управления для реализации заданного преобразования входных переменных в выходные или передаточных функций с определенными параметрами.

Наиболее распространёнными являются линейные законы управления, которые обычно классифицируют на различные виды пропорциональных, интегрирующих, дифференцирующих или PID-регуляторов с соответствующими передаточными функциями:

3. Помехоустойчивость

Под помехоустойчивостью понимают способность системы сохранять рассмотренные выше свойства (устойчивость, точность, закон управления) при воздействии помех различного рода. Различают аддитивные ( , где z — помеха) и мультипликативные ( ) помехи. Очевидно, что аддитивные помехи являются, в определённом смысле, независимыми от сигнала x и могут проявляться как при наличии сигналов, так и при их отсутствии. Мультипликативные помехи непосредственно связаны с сигналом и не могут проявляться при отсутствии такового.

Вопросы борьбы с помехами в системах управления с точки зрения теории управления связаны с изменением динамических свойств соответствующих цепей системы управления.

Представим передаточную функцию как

W =f₁(p)/f₂(p)

Рассмотрим W = f₁/pf₂ = (1/p)f₁/f₂ Первая математическая форма f₁/pf₂ подразумевает ускорение формирования выходного сигнала за счёт дифференцирующего звена. Вторая математическая форма - (1/p)f₁/f₂ - замедление входного сигнала (или помехи) за счёт интегрирующего звена. Эквивалентность этих математических форм означает что для борьбы с помехами могут использоваться обе эти формы. Отметим, что ускорение или замедление соответствующих сигналов с физической точки зрения означает изменение их спектральных характеристик.

Типичным примером минимизации аддитивных помех (например, в системах питания) является использование второй математической формы (интегрирующего звена - емкостей) по соответствующим цепям питания. Это позволяет разнести спектральные характеристики сигналы и помехи.

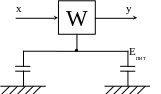
Перечисленные свойства систем управления обычно определяют как показатели качества соответствующей системы. В эти показатели входят, как правило, устойчивость, точность, характер переходных процессов (монотонный или колебательный).

В ряде случаев при колебательных переходных процессах показатель перерегулирования (выброс процесса) имеет самостоятельный смысл и нормируется в качестве дополнительного свойства системы.