§8. Применение рядов в приближенных вычислениях

Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «не берущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.

Примеры:

I. Вычислить приближенно с точностью до 0,0001:

а)

Решение. Для вычисления запишем ряд (2) при , принадлежащем области сходимости :

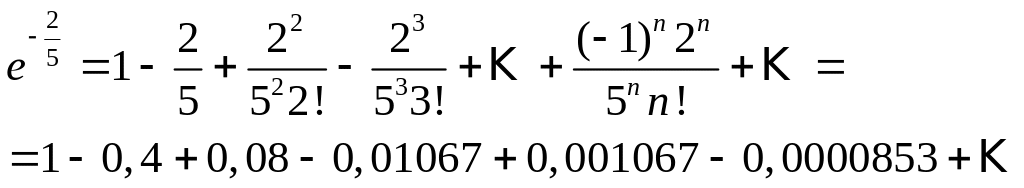
Взяв первые пять членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда мы допустим погрешность , не превышающую первого отброшенного члена (по абсолютной величине), т.е. .

Итак,

б)

Решение. Воспользуемся разложением (10), подставив в него , входящее в область сходимости :

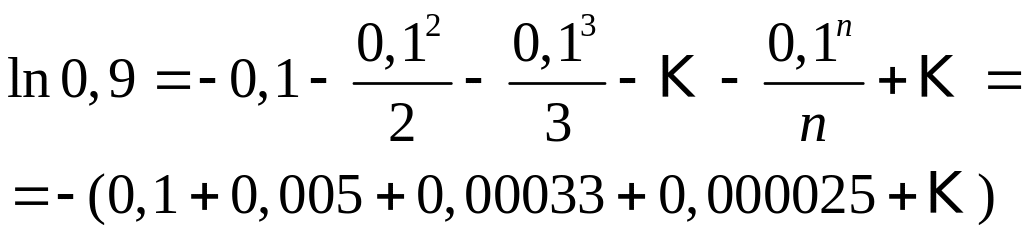
Так как данный числовой ряд не является знакопеременным, то о погрешности нельзя судить по величине первого отбрасываемого члена.

Если в качестве взять сумму первых трех членов, мы допустим погрешность

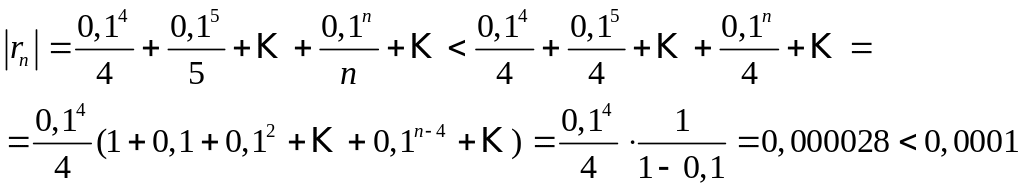(здесь мы учли, что сумма сходящегося геометрического ряда в скобках равна )

Итак,

в)

Решение. Для вычисления запишем ряд (3) при , принадлежащем области сходимости :

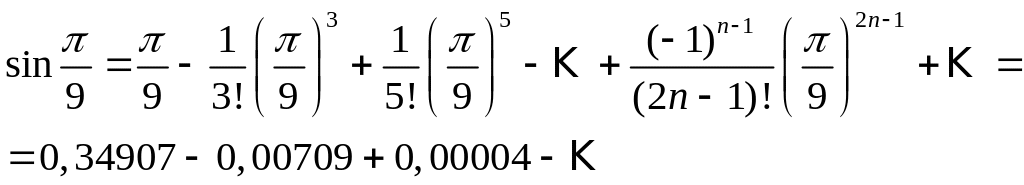
(необходимо взять два члена, так как при этом погрешность ). Итак,

.

II. Вычислить приближенно с точностью до 0,001 следующие интегралы:

a)

Решение. Так как интеграл «не берущийся», «точное» интегрирование здесь невозможно.

Воспользуемся разложением (3). Разделив обе части на , получим

, причем ряд сходится при всех значениях . Интегрируя почленно, получим:

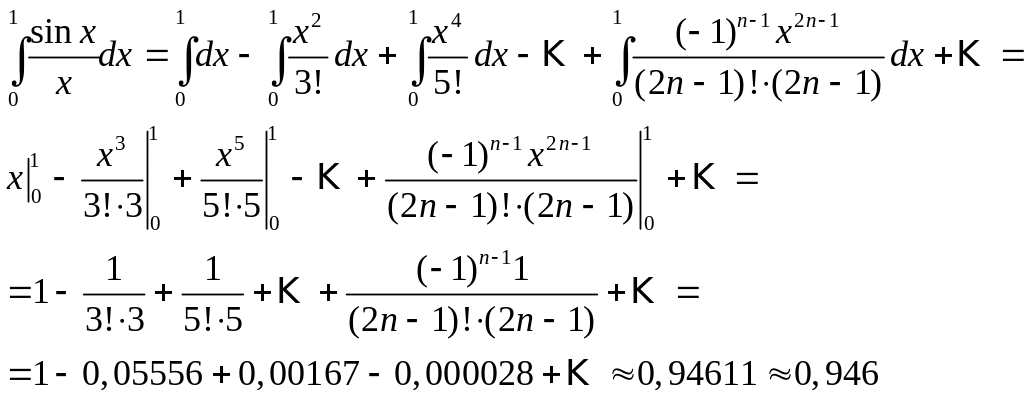
Возьмем первые три члена разложения, т.к. .

Итак,

б)

Решение. Заменив на в разложении (2), получим:

.

Умножая полученный ряд на

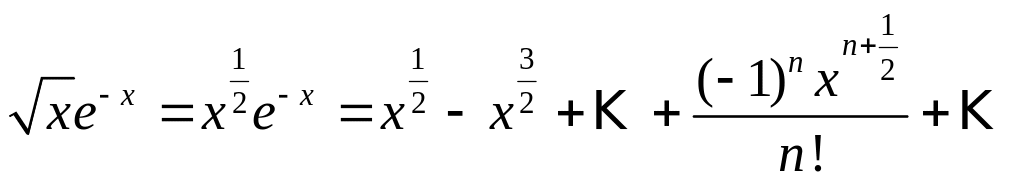
и почленно интегрируя в интервале , принадлежащем интервалу сходимости ряда , имеем:

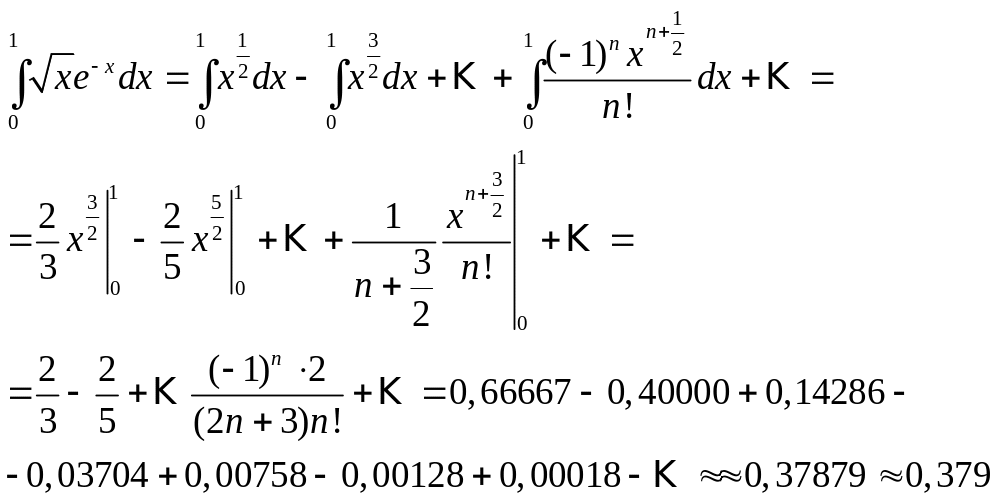
При этом .

Итак, .

Задачи.

Разложить в ряд Маклорена следующие функции, указав промежутки сходимости полученных рядов.

1. 2. 3.

4. 5. 6.

7.

Разложить в ряд Тейлора следующие функции и найти область сходимости полученного ряда.

1. по степеням

2. по степеням

3. по степеням

4. по степеням

5. по степеням

6. по степеням

Вычислить приближенно с точностью до 0,0001:

1. 2. 3. 4.

5. 6.

Вычислить приближенно, взяв первые два члена разложения в ряд подынтегральной функции, и оценить допущенные при этом погрешности:

1. 2.

Подписано в печать 2012 г. Формат 6084/16. Бумага писчая. Отпечатано на ризографе. Уч. изд. листов 2. Тираж 600. Заказ №

Московский государственный университет тонких химических технологий им. М.В.Ломоносова

Издательско-полиграфический центр

117571, Москва, просп. Вернадского, 86.

* Напомним, что степенью степенного выражения называется наибольшая из степеней входящих в него слагаемых, само это слагаемое называется старшим, а его коэффициент называется старшим коэффициентом. Например, у степенного выражения старшее слагаемое имеет степень 1,5, а старший коэффициент равен 5.

44