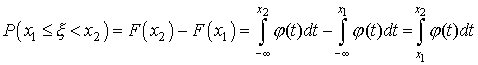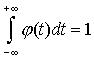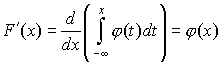Доказательство

Так как в результате   независимых испытаний, проведенных в одинаковых условиях, событие   наступает с вероятностью  , следовательно противоположное ему событие с вероятностью  .

Обозначим   — наступление события   в испытании с номером  . Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате   опытов событие   наступает   раз, тогда остальные  раз это событие не наступает. Событие   может появиться   раз в   испытаниях в различных комбинациях, число которых равноколичеству сочетаний из   элементов по  . Это количество сочетаний находится по формуле:

.

При этом вероятность каждой комбинации равна произведению вероятностей:

.

Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:

, где  .

14 – ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ, ЕЕ СВОЙСТВА.

Реальное содержание понятия «случайная величина» может быть выражено с помощью такого определения: случайной величиной, связанной с данным опытом, называетсявеличина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, причем заранее неизвестно, какое именно. Случайные величины будем обозначать буквами 

Определение. Говорят, что задана дискретная случайная величина   , если указано конечное или счетное множество чисел

и каждому из этих чисел   поставлено в соответствие некоторое положительное число   , причем

Числа   называются возможными значениями случайной величины   , а числа  - вероятностями этих значений (   ).

Таблица

называется законом распределения дискретной случайной величины   .

Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной системе координат строят точки   и соединяют последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины   .

Если возможными значениями дискретной случайной величины   являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли

ОПРЕДЕЛЕНИЕ. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

X	x1	x2	...	xn
P	p1	p2	...	pn

Пример 2. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 тыс. тенге и десять выигрышей по 1тыс. тенге. Найти закон распределения случайных величин Х- стоимости возможного выигрыша для владельца одного лотерейного билета.

Решение: Напишем возможные значения х: х₁=50, х₂=1, х₃=0. Вероятности этих возможных значений таковы: Р₁=1/100=0,01, Р₂=10/100=0,1, Р₃=89/100=0,89. Напишем искомый закон распределения:

X	50	1	0
P	0.01	0.1	0.89

Контроль: 0,01+0,1+0,89=1.

15 – МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ ДИСПЕРИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

ОПРЕДЕЛЕНИЕ. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина Х может принимать только значения х₁, х₂, х₃,...,х_nвероятности которых соответственно равны p₁, p₂, p₃,...,p_n. Тогда математическое ожидание М(х) случайной величины Х определяется равенством:

M(x)=х₁p₁+х₂p₂+...+х_np_n

Если дискретная случайная величина Х принимает счетное множество возможных значений, то:

причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Пример 3. Найти математическое ожидание случайной величины Х, зная закон ее распределения:

X	3	5	2
P	0.1	0.6	0.3

Решение: Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности: М(х)=3 .

Свойства математического ожидания

1. Математическое ожидание постоянной величины равно самой постоянной М(С)=С.  2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X)  3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY)=M(X)•M(Y).  4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: M(X+Y)=M(X)+M(Y).

Пример 4. Независимые случайные величины заданы следующими законами распределения:

X	5	2	4
P	0.6	0.1	0.3

Y	7	9
P	0.8	0.2

Найти математическое ожидание случайных величин Х, Y.

Решение: Найдем математическое ожидание каждой из данных величин:

M(X)=5•0.6+2•0.1+4•0.3=4.4  M(Y)=7•0.8+9•0.9=9.4

Теорема. Математическое ожидание М(х) числа появлений событий А в n независимых испытаниях равно произведению этих испытаний на вероятность появления событий в каждом испытании: M(x)=np.

Пусть Х- случайная величина и М(Х) – ее математическое ожидание. Рассмотрим в качестве новой случайной величины разность Х-М(Х).

ОПРЕДЕЛЕНИЕ. Отклонением называют разность между случайной величиной и ее математическим ожиданием.

Отклонение имеет следующий закон распределения:

X-M(x)	X1-M(x)	X2-M(x)	...	Xn-M(x)
P	p1	p2	...	pn

Теорема. Математическое ожидание отклонения равно нулю: M(X-M(x)=0).

Пример 5. Задан закон распределения дискретной случайной величины Х:

X	1	2
P	0.2	0.8

Доказать, что математическое ожидание отклонения равно нулю.

Решение: Найдем математическое ожидание Х: M(x)=1•0.2+2•0.8=1.8  Найдем возможные значения отклонения, для чего из возможных значений Х вычтем математическое ожидание M(x):1-18=-0.8; 2-1.8=0.2 Напишем закон распределения отклонения:

X-M(x)	-0.8	0.2
P	0.2	0.8

Найдем математическое ожидание отклонения: M(X-M(x))=(-0.8)•0.2+0.2•0.8=0  На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.

ОПРЕДЕЛЕНИЕ. Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

D(x)=M[X-M(x)]² (2)

Пример 6. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:

X	1	2	5
P	0.3	0.5	0.2

Решение: Найдем математическое ожидание:  [X₁-M(x)]²=(1-2.3)²=1.69  [X₂-M(x)]²=(2-2.3)²=0.09  [X₃-M(x)]²=(5-2.3)²=7.29

Напишем закон распределения квадрата отклонения:

[X-M(x)]2	1.69	0.09	7.29
P	0.3	0.5	0.2

По определению, D(x)=1.69•0.3+0.09•0.5+7.29•0.2=2.01

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

D(x)=M(x²)-[M(x)]² (3)

Пример 7. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:

X	2	3	5
P	0.1	0.6	0.3

Решение: Найдем математическое ожидание М(х): M(x)=2•0.1+3•0.6+5•0.3=3.5

Напишем закон распределения случайной величины X²

X2	4	9	25
P	0.1	0.6	0.3

Найдем математическое ожидание M(x²): M(x²)=4•0.1+9•0.6+25•0.3=13.5

Искомая дисперсия D(x)=M(x²)-[M(x)]²=13.3-(3.5)²=1.05

Свойства дисперсии:

1. Дисперсия постоянной величины С равна нулю: D(C)=0  2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат. D(Cx)=C²D(x)  3. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин. D(X₁+X₂+...+X_n)=D(X₁)+D(X₂)+...+D(X_n)  4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании D(X)=npq

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратичное отклонение.

ОПРЕДЕЛЕНИЕ. Средним квадратичным отклонением случайной величины Х называют квадратный корень из дисперсии:

σ(X)=√D(X) (4)

16 – БИНОМИАЛЬНЫЙ ЗАКОН

 Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность  , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону   можно назвать числом появле­нии события в n независимых опытах.

Пусть имеется некое событие A. Вероятность появления события A равна p, вероятность непоявления события A равна 1 – p, иногда ее обозначают как q. Пусть n — число испытаний, m — частота появления события A в этих n испытаниях.

Известно, что суммарная вероятность всех возможных комбинаций исходов равна единице, то есть:

1 = pⁿ + n · p^n – 1 · (1 – p) + C_n^n – 2 · p^n – 2 · (1 – p)² + … + C_n^m · p^m · (1 – p)^n – m + … + (1 – p)ⁿ.

pn — вероятность того, что в n испытаниях событие A произойдет n раз; n · pn – 1 · (1 – p) — вероятность того, что в n испытаниях событие A произойдет(n – 1) раз и не произойдет 1 раз; Cnn – 2 · pn – 2 · (1 – p)2 — вероятность того, что в n испытаниях событие Aпроизойдет (n – 2) раза и не произойдет 2 раза; Pm = Cnm · pm · (1 – p)n – m — вероятность того, что в n испытаниях событие Aпроизойдет m раз и не произойдет (n – m) раз; (1 – p)n — вероятность того, что в n испытаниях событие A не произойдет ни разу;  — число сочетаний из n по m.

Математическое ожидание M биномиального распределения равно:

M = n · p,

где n — число испытаний, p — вероятность появления события A.

Среднеквадратичное отклонение σ:

σ = sqrt(n · p · (1 – p)).

17 – ЗАКОН ПУАССОНА.

Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и приp –> 0 (редкие события)).

Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:

где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения

P_m = C_n^m · p^m · (1 – p)^n – m

может быть написан, если положить p = a/n, в виде

или

Так как p очень мало, то следует принимать во внимание только числа m, малые по сравнению сn. Произведение

весьма близко к единице. Это же относится к величине

Величина

очень близка к e^–a. Отсюда получаем формулу:

Пример. В ящике находится n = 100 деталей, как качественных, так и бракованных. Вероятность достать бракованное изделие составляет p = 0.01. Допустим, что мы вынимаем изделие, определяем, бракованное оно или нет, и кладем его обратно. Поступая таким образом, получилось, что из 100 изделий, которые мы перебрали, два оказались бракованными. Какова вероятность этого?

По биномиальному распределению получаем:

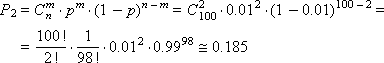
По распределению Пуассона получаем:

Как видно, величины получились близкими, поэтому в случае редких событий вполне допустимо применять закон Пуассона, тем более что он требует меньших вычислительных затрат.

18 – НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ, ИХ ВЗАИМОСВЯЗЬ И СВОЙСТВА.

 Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:   

   Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х.     Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.     Случайная величина   называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция*  , удовлетворяющая для любых значений x равенству

(22)

   Функция   называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x₁<x₂, то на основании формул (20) и (22) имеем

(23)

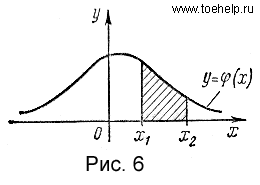
   Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств   равна площади криволинейной трапеции с основанием[x₁,x₂], ограниченной сверху кривой   (рис. 6).

   Так как  , а на основании формулы (22)   

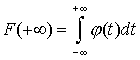
   , то

(24)

   Пользуясь формулой (22), найдем   как производную интеграла по переменной верхней границе, считая плотность распределения   непрерывной**:

(25)

   Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция   непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.     На основании формулы (23), полагая x₁=x,  , имеем   

   В силу непрерывности функции F(х) получим, что   

   Следовательно   

   Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.     Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств   

 ,   ,   , 

   Имеют одинаковую вероятность, т.е.   

   В самом деле, например,   

   так как       Замечание. Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение x₁ как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение x₁. Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.     Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.     Пример. Плотность распределения непрерывной случайной величины задана следующим образом:   

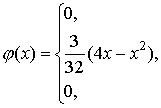
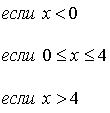
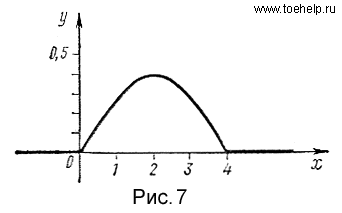
   График функции   представлен па рис. 7. Определить вероятность того, что случайная величина   примет значение, удовлетворяющее неравенствам  .Найти функцию распределения заданной случайной величины. (Решение)

   Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному и нормальному распределениям.