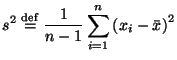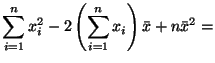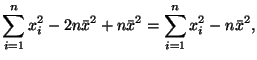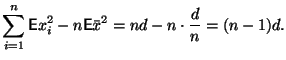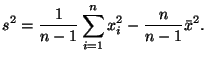Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российская таможенная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matematika.doc

Скачиваний:

Добавлен:

09.11.2019

Размер:

1.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Неравенство чебышева

Рассмотрим сначала вспомогательные теоремы: лемму и неравенство Чебышева, с помощью которых легко доказывается закон больших чисел в форме Чебышева.

Лемма (Чебышев).

Если среди значений случайной величины Х нет отрицательных, то вероятность того, что она примет какое-нибудь значение, превосходящее положительное число А , не больше дроби, числитель которой — математическое ожидание случайной величины, а знаменатель - число А:

Доказательство. Пусть известен закон распределения случайной величины Х:

(i = 1, 2, ..., ), причем значения случайной величины мы считаем расположенными в возрастающем порядке.

По отношению к числу А значения случайной величины разбиваются на две группы: одни не превосходят А, а другие больше А. Предположим, что к первой группе относятся первые значений случайной величины ( ).

Так как , то все члены суммы неотрицательны. Поэтому, отбрасывая первые слагаемых в выражении получим неравенство:

Поскольку

то

Далее,

что и требовалось доказать.

Случайные величины могут иметь различные распределения при одинаковых математических ожиданиях. Однако для них лемма Чебышева даст одинаковую оценку вероятности того или иного результата испытания. Этот недостаток леммы связан с ее общностью: добиться лучшей оценки сразу для всех случайных величин невозможно.

Неравенство Чебышева.

Вероятность того, что отклонение случайной величины от ее математического ожидания превзойдет по абсолютной величине положительное число , не больше дроби, числитель которой - дисперсия случайной величины, а знаменатель - квадрат

Доказательство. Поскольку случайная величина, которая не принимает отрицательных значений, то применим неравенство из леммы Чебышева для случайной величины при :

что и требовалось доказать.

Следствие. Поскольку

то

- другая форма неравенства Чебышева

Примем без доказательства факт, что лемма и неравенство Чебышева верны и для непрерывных случайных величин.

Неравенство Чебышева лежит в основе качественных и количественных утверждений закона больших чисел. Оно определяет верхнюю границу вероятности того, что отклонение значения случайной величины от ее математического ожидания больше некоторого заданного числа. Замечательно, что неравенство Чебышева дает оценку вероятности события для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.

Теорема. (Закон больших чисел в форме Чебышева)

Если дисперсии независимых случайных величин ограничены одной константой С, а число их достаточно велико, то как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий не превзойдет по абсолютной величине данного положительного числа , каким бы малым оно ни было:

Теорему примем без доказательства.

Следствие 1. Если независимые случайные величины имеют одинаковые, равные , математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число их достаточно велико, то, сколько бы мало на было данное положительное число , как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от не превзойдет по абсолютной величине .

То, что за приближенное значение неизвестной величины принимают среднюю арифметическую результатов достаточно большого числа ее измерений, произведенных в одних и тех же условиях, можно обосновать этой теоремой. Действительно, результаты измерений являются случайными, так как на них действует очень много случайных факторов. Отсутствие систематических ошибок означает, что математические ожидания отдельных результатов измерений одинаковые и равны . Следовательно, по закону больших чисел средняя арифметическая достаточно большого числа измерений практически будет как угодно мало отличаться от истинного значения искомой величины.

(Напомним, что ошибки называются систематическими, если они искажают результат измерения в одну и ту же сторону по более или менее ясному закону. К ним относятся ошибки, появляющиеся в результате несовершенства инструментов (инструментальные ошибки), вследствие личных особенностей наблюдателя (личные ошибки) и др.)

Следствие 2. (Теорема Бернулли.)

Если вероятность наступления события А в каждом из независимых испытаний постоянна, а их число достаточно велико, то сколь угодно близка к единице вероятность того, что частота появления события как угодно мало отличается от вероятности его появления:

Теорема Бернулли, утверждает, что если вероятность события одинакова во всех испытаниях, то с увеличением числа испытаний частота события стремится к вероятности события и перестает быть случайной.

На практике сравнительно редко встречаются опыты, в которых вероятность появления события в любом опыте неизменна, чаще она разная в разных опытах. К схеме испытаний такого типа относится теорема Пуассона:

Следствие 3. (Теорема Пуассона.)

Если вероятность появления события в -ом испытании не меняется, когда становятся известными результаты предыдущих испытаний, а их число достаточно велико, то сколь угодно близка к единице вероятность того, что частота появления события как угодно мало отличается от средней арифметической вероятностей :

Теорема Пуассона утверждает, что частота события в серии независимых испытаний стремится к среднему арифметическому его вероятностей и перестает быть случайной.

В заключение заметим, что ни одна из рассмотренных теорем не дает ни точного, ни даже приближенного значения искомой вероятности, а указывается лишь нижняя или верхняя граница ее. Поэтому, если требуется установить точное или хотя бы приближенное значение вероятностей соответствующих событий, возможности этих теорем весьма ограничены.

Приближенные значения вероятностей при больших значениях можно получить только с помощью предельных теорем. В них или на случайные величины налагаются дополнительные ограничения (как это имеет место, например, в теореме Ляпунова), или рассматриваются случайные величины определенного вида (например, в интегральной теореме Муавра—Лапласа).

Теоретическое значение теоремы Чебышева, являющейся весьма общей формулировкой закона больших чисел, велико. Однако если мы будем применять ее при решении вопроса о возможности применить закон больших чисел к последовательности независимых случайных величин, то при утвердительном ответе теорема часто будет требовать, чтобы случайных величин было гораздо больше, чем необходимо для вступления в силу закона больших чисел. Указанный недостаток теоремы Чебышева объясняется общим характером ее. Поэтому желательно иметь теоремы, которые точнее указывали бы нижнюю (или верхнюю) границу искомой вероятности. Их можно получить, если наложить на случайные величины некоторые дополнительные ограничения, которые для встречающихся на практике случайных величин обычно выполняются.

26 – ВЫБОРОЧНАЯ СРЕДНЯЯ И ВЫБОРОЧНАЯ ДИСПЕРСИЯ

Иногда исследователь ставит перед собой более конкретную проблему: как, основываясь на выборке, оценить интересующие его числовые характеристики неизвестного распределения, не прибегая к приближению этого распределения как такового, то есть без построения выборочных функций распределения, гистограмм и т.п.

В данном параграфе мы обсудим простые (но, как увидим в дальнейшем, весьма хорошие) выборочные аппроксимации для математического ожидания и дисперсии. Замечательно то, что они применимы в очень общей ситуации. Мы будем предполагать, что независимая выборка взята из неизвестного распределения, у которого существует математическое ожидание и дисперсия (обозначим эти неизвестные значения через и соответственно).

Определение 6.2

Величины, вычисляемые по выборке,

(29)

(30)

называются выборочным средним и выборочной дисперсией.

Следует особо подчеркнуть, что определенные выше величины зависят только от выборки. Следующее предложение объясняет, почему естественно считать выборочным аналогом математического ожидания, а -- выборочным аналогом дисперсии.

Предложение 6.1

Математические ожидания и совпадают с оцениваемыми неизвестными величинами:

(31)

Дисперсия стремится к нулю при росте объема выборки.

Доказательство.

Используя линейность математического ожидания, получим

Так как выборка независимая, то . Следовательно, при .

Покажем теперь, что . Первое замечание состоит в том, что не зависит от сдвига всех элементов выборки на одну и ту же константу, то есть, значения выражения (30) для выборок и одинаковы. Поэтому без ограничения общности мы будем считать, что . При этом предположении

Теперь, проводя очевидные преобразования и применяя свойства математического ожидания, легко получаем необходимое утверждение



			(32)

Это утверждение свидетельствует о том, что и являются ``качественными приближениями'' для неизвестных величин и . Свойство (31) называетсянесмещенностью. Тот факт, что дисперсия исчезает с увеличением объема выборки дает основание для вывода о том, что, чем больше данных измерений мы возьмем для статистической обработки, тем точнее будут наши выводы.

Замечание 6.4

Для оценивания дисперсии по выборке может быть использована также функция

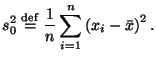
Формально ее можно получить, заменив в определении дисперсии оператор математического ожидания средним арифметическим. Ясно, что величина в отличие от является смещенной: . Хотя для больших выборок эта смещенность не очень существенна.

Предложение 6.2

При росте объема выборки

Доказательство.

Как и при доказательстве Предложения 6.1 без ограничения общности будем считать, что . При этом предположении . Из (32) вытекает, что

(33)

Применяя закон больших чисел в форме Хинчина к последовательности , имеем

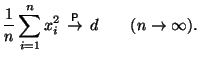
В силу предположения по закону больших чисел при . Следовательно (см. Упражнение 2.10), . Отсюда вытекает, что .

Замечание 6.5

Здесь мы воспроизводим замечание о вычислениях, приведенное в [12, с. 116]. Из соотношения (33) вытекает следующее представление для :

(34)

Математически формулы (30) и (34) дают одно и то же значение. Но, если нам необходимовручную вычислить выборочную дисперсию, то следует это делать только по формуле (30), так как вычисления по формуле (34) потребовали бы учета намного большего числа значащих цифр, чем в случае применения формулы (30).

Имеется большое число практически важных приемов, призванных облегчить вычислительную работу с конкретными числовыми выборками. Для знакомства с ними рекомендуем читателю обратиться к книге [11].

В настоящее время существует много прикладных компьютерных программ, которые можно и нужно использовать для обработки числовых данных. С некоторыми наиболее популярными специализированными статистическими пакетами (Stadia, StatGraphics) можно познакомиться по книге [13], к которой также приводится их сравнение. Для статистической обработки небольших массивов данных вполне подойдет любой хороший универсальный математический пакет (Mathematica, Maple, Matlab).

Пример 6.5

Вычислим выборочное среднее и выборочную дисперсию для числовых данных Примера 6.4 на странице . Подставив данные в формулы (29) и (30), найдем для выборки

и для выборки

Полезной величиной является также корень из выборочной дисперсии как оценка среднеквадратичного уклонения:

27 – Интервальная оценка параметров распределения. Доверительный интервал.

Сущность задачи интервального оценивания параметров

Интервальный метод оценивания параметров распределения случайных величин заключается в определении интервала (а не единичного значения), в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра. Интервальная оценка характеризуется двумя числами – концами интервала, внутри которого предположительно находится истинное значение параметра. Иначе говоря, вместо отдельной точки для оцениваемого параметра можно установить интервал значений, одна из точек которого является своего рода "лучшей" оценкой. Интервальные оценки являются более полными и надежными по сравнению с точечными, они применяются как для больших, так и для малых выборок. Совокупность методов определения промежутка, в котором лежит значение параметра Т, получила название методов интервального оценивания. К их числу принадлежит метод Неймана.

Постановка задачи интервальной оценки параметров заключается в следующем [3, 11].

Имеется: выборка наблюдений (x₁, x₂, …, x_n) за случайной величиной Х. Объем выборки n фиксирован.

Необходимо с доверительной вероятностью  = 1–  определить интервал t₀ – t₁ (t₀ < t₁), который накрывает истинное значение неизвестного скалярного параметра Т(здесь, как и ранее, величина Т является постоянной, поэтому некорректно говорить, что значение Т попадает в заданный интервал).

Ограничения: выборка представительная, ее объем достаточен для оценки границ интервала.

Эта задача решается путем построения доверительного утверждения, которое состоит в том, что интервал от t₀ до t₁ накрывает истинное значение параметра Т с доверительной вероятностью не менее  . Величины t₀ и t₁ называются нижней и верхней доверительными границами (НДГ и ВДГ соответственно). Доверительные границы интервала выбирают так, чтобы выполнялось условие P(t₀  t₁) =  . В инженерных задачах доверительную вероятность  назначают в пределах от 0,95 до 0,99. В доверительном утверждении считается, что статистики t₀ и t₁ являются случайными величинами и изменяются от выборки к выборке. Это означает, что доверительные границы определяются неоднозначно, существует бесконечное количество вариантов их установления.

На практике применяют два варианта задания доверительных границ:

устанавливают симметрично относительно оценки параметра, т.е. t₀=  – Е , t₁=  + Е , где Е выбирают так, чтобы выполнялось доверительное утверждение. Следовательно, величина абсолютной погрешности оценивания Е равна половине доверительного интервала;

устанавливают из условия равенства вероятностей выхода за верхнюю и нижнюю границу Р(Т >  + Е₁_,_)=Р(Т <  – Е_2,_)= /2. В общем случае величина Е_1,_не равнаЕ_2,_. Для симметричных распределений случайного параметра  в целях минимизации величины интервала значения Е_1,_и Е_2,_выбирают одинаковыми, следовательно, в таких случаях оба варианта эквивалентны.

Нахождение доверительных интервалов требует знания вида и параметров закона распределения случайной величины  . Для ряда практически важных случаев этот закон можно определить из теоретических соображений.

Общий метод построения доверительных интервалов

Метод позволяет по имеющейся случайной выборке построить функцию и(Т,  ), распределенную асимптотически нормально с нулевым математическим ожиданием и единичной дисперсией. В основе метода лежат следующие положения. Пусть:

f(х,  ) – плотность распределения случайной величины Х;

ln [L(x,  )] – логарифм функции правдоподобия;

;

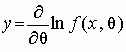А²=М(у)²– дисперсия у.

Если математическое ожидание М(у) = 0 и дисперсия у конечна, то распределение случайной величины w = 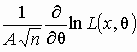асимптотически нормально с параметрами 0 и 1 при п  .

Пример 4.4. Построить доверительный интервал с надежностью  =1–  для оценки  ₁ математического ожидания m₁случайной величины х, имеющей экспоненциальное распределение с функцией плотности f(x, l) = lехр(– lх).

Решение. Известно, что для экспоненциального закона распределения математическое ожидание т₁ = 1/l, а дисперсия т₂ = 1/l². Обозначим через  оценку параметра l. Определим оценку математического ожидания  ₁, вспомогательную переменную у, производную от логарифма функции правдоподобия:

 ₁ = (х₁+ х₂+ … + х_п)/п = 1/ ; М( ) = l; т₁ = М(1/ );

у = ;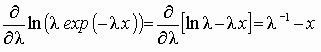

Оценка  ₁ параметра т₁ является состоятельной и несмещенной, следовательно: М(у)=М( ^–1– х) = 0; значение А²= М( ^–1 – х)² = ^–2 конечно. Тогда случайная величина

w =

распределена нормально с параметрами 0 и 1.

Нормальное распределение симметрично, поэтому границы интервала следует выбрать симметрично относительно нулевой точки. Вероятность  =1 –  того, что модуль величины w не превысит некоторого заданного значения  , составит

где Ф( ) – значение функции нормального распределения в точке  .

Величина  равна квантили u_1–__/2 стандартного нормального распределения уровня 1–  /2. Значение абсолютной погрешности оценивания E = | m₁–  ₁| = /( n^0,5) =u_1–__/2/( n^0,5). Итак, имея достаточный объем выборки ЭД и задаваясь определенным уровнем надежности  можно определить доверительный интервал t₀ =  ₁ – Е, t₁ = ₁ + Е, который с заданной вероятностью содержит неизвестный параметр т₁.

Аналогичные результаты для некоторых параметров распределения можно получить, используя более простые рассуждения.

Доверительный интервал для математического ожидания

Пусть по выборке достаточно большого объема, n > 30, и при заданной доверительной вероятности 1–  необходимо определить доверительный интервал для математического ожидания m₁, в качестве оценки которого используется среднее арифметическое .

Закон распределения оценки математического ожидания близок к нормальному (распределение суммы независимых случайных величин с конечной дисперсией асимптотически нормально). Если потребовать абсолютную надежность оценки математического ожидания, то границы доверительного интервала будут бесконечными [–  ,  ]. Выбор любых более узких границ связан с риском ошибки, вероятность которой определяется уровнем значимости  . Интерес представляет максимальная точность оценки, т.е. наименьшее значение интервала. Для симметричных функций минимальный интервал тоже будет симметричным относительно оценки  ₁. В этом случае выражение для доверительной вероятности имеет вид P(|  ₁– m₁|Е) = 1–  , где Е – абсолютная погрешность оценивания.

Нормальный закон полностью определяется двумя параметрами – математическим ожиданием и дисперсией. Величина  ₁ является несмещенной, состоятельной и эффективной оценкой математического ожидания, поэтому ее значение принимаем за значение математического ожидания. Определим оценку дисперсии случайного параметра  ₁, учитывая, что этот параметр равен среднему арифметическому одинаково распределенных случайных величин x_i (следовательно, их дисперсии D(x_i) одинаковы и равны  ₂)

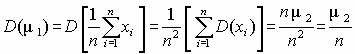Итак, случайная величина  ₁ распределена по нормальному закону с параметрами  ₁ и  ₂/ n. Для установления необходимых соотношений целесообразно перейти к центрированным и нормированным величинам. Выражение  ₁– m₁ можно трактовать как центрирование случайной величины  ₁. Нормирование осуществляется делением на величину среднеквадратического отклонения оценки  ₁

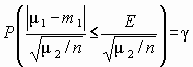Для стандартизованной величины вероятность соблюдения неравенства определяется по функции нормального распределения

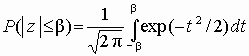= Ф( ) – Ф(– ) = –1+ 2Ф( )=1–  ,

где . Значение  равно квантили u_1–__/2 стандартного нормального распределения уровня 1–  /2. В частности, уровням надежности 0,9, 0,95 и 0,99 соответствуют значения допустимого отклонения u_1–__/2 величины z, равные 1,64, 1,96 и 2,58 соответственно. Окончательно можно записать

u²_1–__/2 = nЕ²/ ₂ .

(4.3)

Нетрудно заметить, что это выражение аналогично по своему содержанию формуле, полученной с использованием общего метода построения доверительного интервала.

При фиксированном объеме выборки из (4.3) следует, что чем больше доверительная вероятность 1–  , тем шире границы доверительного интервала (тем больше ошибка в оценке математического ожидания). Это равенство позволяет определить необходимый объем выборки для получения оценки математического ожидания с заданной надежностью и требуемой точностью (погрешностью): n= ₂u²_1–__/2/Е². Если перейти к относительной погрешности  = Е/ ₁, то

n =  ₂u²_1–__/2 /( ²^₁²).

(4.4)

Таким образом, чтобы снизить относительную погрешность на порядок, необходимо увеличить объем выборки на два порядка. Приведенная формула часто используется в статистическом моделировании для определения необходимого количества испытаний модели.

Во многих случаях предположение о нормальном распределении случайной величины  ₁ становится приемлемым при n > 4 и вполне хорошо оправдывается при n >10. Оценка  ₁ вполне пригодна для применения вместо m₁. Но не так обстоит дело с дисперсией, правомочность ее замены на  ₂ не обоснована даже в указанных случаях. При небольшом объеме выборки, n < 30, закон распределения оценки дисперсии  ₂ принимать за нормальный неоправданно. Ее распределение следует аппроксимировать распределением хи-квадрат как суммы квадратов центрированных величин (хи-квадрат распределение сходится к нормальному при количестве слагаемых, превышающем 30). Но это утверждение обосновано только для случая, когда случайная величина Х распределена нормально.

С учетом сделанных допущений величина z будет подчиняться закону распределения Стьюдента с n–1 степенями свободы (одна степень свободы использована для определения оценки дисперсии). Распределение Стьюдента симметричное, поэтому полученное соотношение между точностью, надежностью оценки и объемом выборки сохраняется, меняются только значения квантилей. Вместо квантили нормального распределения u_1–__/2 следует взять квантиль t_1–__/2(n–1) распределения Стьюдента с (n–1) степенями свободы. Значения критических точек распределения Стьюдента для некоторых вероятностей и различных степеней свободы, представлены в табл. П.4. Как можно видеть из табл. П.4, квантили распределения Стьюдента больше квантилей нормального распределения того же уровня надежности при малом n. Иначе говоря, применение нормального распределения при небольшом объеме выборки ЭД приводит к неоправданному завышению точности оценки.

Пример 4.5. Определить с надежностью  = 0,9 доверительный интервал для математического ожидания случайной величины, выборка которой представлена вариационным рядом, табл. 2.3.

Решение. Ранее были определены оценки  ₁ =27,51 и  ₂=0,91. Интервал двусторонний, симметричный  = 0,1. Объем выборки можно считать большим, поэтому воспользуемся нормальным распределением, тогда u_0,95 = 1,96. Допустимое отклонение

Е = u_0,95( ₂/n)^0,5 =1,96 (0,91/44)^0,5= 0,28.

С вероятностью 0,9 НДГ интервала составит t₀=27,51– 0,28=27,23, ВДГ интервала t₁= 27,51 + 0,28 = 27,79. Другими словами, с вероятностью 0,9 значение математического ожидания лежит в пределах от 27,23 до 27,79.

28 – ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ.