Элементарное событие

В теории вероятностей элементарные события или события-атомы — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один. Множество всех элементарных событий обычно обозначается  .

Всякое подмножество множества   элементарных событий называется случайным событием. Говорят, что в результате эксперимента произошло случайное событие  , если (элементарный) исход эксперимента является элементом  .

В определении вероятностного пространства на множестве случайных событий вводится сигма-аддитивная конечная мера, называемая вероятностью.

Элементарные события могут иметь вероятности, которые строго положительны, нули, неопределенны, или любая комбинация из этих вариантов. Например, любое дискретноевероятностное распределение определяется вероятностями того, что может быть названо элементарными событиями. Напротив, все элементарные события имеют вероятность нуль длянепрерывного распределения. Смешанные распределения, не будучи ни непрерывными, ни дискретными, могут содержать атомы, которые могут мыслиться как элементарные (то естьсобытия-атомы) события с ненулевой вероятностью. В теории меры в определении вероятностного пространства вероятность произвольного элементарного события не могла быть определена до тех пор, пока математики не увидели различие между пространством исходов S и событиями, которые представляют интерес, и которые определяются как элементы σ-алгебры событий из S.

Формально говоря, элементарное событие — это подмножество пространства исходов случайного эксперимента, которое состоит только из одного элемента; то есть элементарное событие — это всё ещё множество, но не сам элемент. Однако элементарные события обычно записываются как элементы, а не как множества с целью упрощения, когда это не может вызвать недоразумения.

Примеры

Примеры пространств исходов эксперимента,  , и элементарных событий:

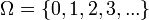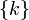• Если объекты счётны, а пространство исходов   (натуральные числа), то элементарные события — это любые множества  , где  .

• Если монета бросается дважды, 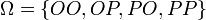 ,   для орла, а   для решки, то элементарные события:  ,  ,   и  .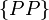

• Если 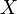  — это нормально распределенные случайные величины, 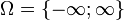 , реальные числа, то элементарные события — любые множества  , где  . Этот пример показывает, что непрерывное вероятностное распределение не определяется вероятностями событий-атомов, поскольку здесь вероятности всех элементарных событий равны нулю.

Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом  . Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом  .

Аксиоматическое определение вероятности. Пусть задано пространство элементарных событий  Е  и каждому событию  А   Е  поставлено в соответствие единственное число Р ( А ) такое, что:

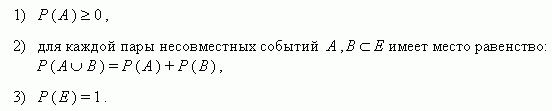
Тогда говорят, что на событиях в множестве Е задана вероятность, а число Р ( А ) называется вероятностью события  А .

Аксиоматическое определение вероятности.

Def: говорят, что на алгебре событий F задана вероятность. Распределение вероятностей, если каждому событию поставлено в соответствие число Р(А), называют вероятностью события А так, что выполнены аксиомы:

1) 

2) 

3) Если A1…Ak попарно несовместны, то вероятность их суммы равна сумме вероятностей.

Поскольку  , то  .

Следовательно,  .

8- КЛАССИЧЕСКОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО

Вероятность события. Классическое определение вероятности

Пусть = { ₁,  ₂, …,  _s} - произвольное конечное пространство элементарных событий, A - событие, состоящее из k элементарных событий: A={ _i1,  _i2, …,  _ik}, 1   i₁   i₂  …  i _k  s, k = 1, 2,…, s, и пусть  . Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество   состоит из всех подмножеств множества  :  ). Таково классическое определение вероятности события A.

Принята следующая формулировка классического определения вероятности: вероятностью события A называется отношение числа исходов, благоприятствующих A, к общему числу исходов.

Из приведенных определений следует: P( )=0,  ,  .

9 – ОТНОСИТЕЛЬНАЯ ЧАСТОТА СОБЫТИЯ, ЕЕ СВОЙСТВА.

Возможность наступления случайного события А можно оценить, проведя серию из “n” независимых испытаний. Пусть число наступлений события составило “m”.

Относительной частотой события А в “n” независимых испытаний называют отношение числа “m” (наступлений А) к числу “n” (общее число испытаний):

.

Относительная частота – послеопытная характеристика возможности события А .

Относительная частота обладает следующими свойствами:

1)  .

2)  .

3) Если   попарно несовместны, то 

Относительная частота обладает статистической устойчивостью (при большом числе испытаний её значения к одному и тому же числу).

Вывод: из свойства статистической устойчивости: существует доопытная характеристика (в каждом эксперименте) возможности события А, значение которой не зависит от проведения серии испытаний, а обусловлено самим комплексом условий. Доопытную характеристику события А называют вероятностью.

Аксиоматическое определение вероятности.

Def: говорят, что на алгебре событий F задана вероятность. Распределение вероятностей, если каждому событию поставлено в соответствие число Р(А), называют вероятностью события А так, что выполнены аксиомы:

1) 

2) 

3) Если A1…Ak попарно несовместны, то вероятность их суммы равна сумме вероятностей.

Поскольку  , то  .

Следовательно, 

Def: Тройку  называют вероятностным пространством случайного эксперимента.

Вероятностная функция на алгебре событий может быть задана по-разному.

Основным способом задания вероятностей на алгебре событий является статистический, когда вероятность событий принимается равной их относительной частоте.

10 – ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Теорема сложения вероятностей формулируется следующим образом.

Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:

.      (3.2.1)

Докажем теорему сложения вероятностей для схемы случаев. Пусть возможные исходы опыта сводятся к совокупности случаев, которые мы для наглядности изобразим в виде n точек:

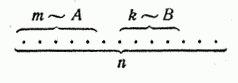
Предположим, что из этих случаев   благоприятны событию , а  – событию . Тогда

Так как события   и  несовместимы, то нет таких случаев, которые благоприятны и , и  вместе. Следовательно, событию   благоприятны   случаев и

Подставляя полученные выражения в формулу (3.2.1), получим тождество. Теорема доказана.

Обобщим теорему сложения на случай трех событий. Обозначая событие   буквой  , и присоединяя к сумме еще одно событие  , легко доказать, что

Очевидно, методом полной индукции можно обобщить теорему сложения на произвольное число несовместных событий. Действительно, предположим, что она справедлива для n событий:

и докажем, что она будет справедлива для   событий:

Обозначим:

Имеем:

.

Но так как для n событий мы считаем теорему уже доказанной, то

,

откуда

,

что и требовалось доказать.

11 - Условная вероятность. Теорема умножения вероятностей.

Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В.     Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:   

	1-я монета	2-я монета
1-й исход	герб	герб
2-й исход	герб	надпись
3-й исход	надпись	герб
4-й исход	надпись	надпись

   Таким образом, P(герб,герб)=1/4.     Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:   

	1-я монета	2-я монета
1-й исход	герб	герб
2-й исход	герб	надпись

   При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях Р(герб,герб)=1/2. Обозначим через А появление двух гербов, а через В— появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло.     Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А).     Таким образом, Р(A)=1/4; PB(А)=1/2     Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.

P(AB)=P(A)PA(B)

(4)

   Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2, ..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает

;  ; 

   Таким образом,

   Поменяв местами A и B, аналогично получим

(5)

   Из формул (4) и (5) имеем

(6)

   Теорема умножения легко обобщается на любое , конечное число событий. Так, например, в случае трех событий A1, A2, A3 имеем *

   В общем случае

(7)

   Введем теперь следующее определение.     Два события A и B называются независимыми, если предположение о том, что произошло одно из них, не изменяет вероятность другого, т. е. если

и

(8)

   Из соотношения (6) вытекает, что из двух равенств (8) одно является следствием другого.     Пусть, например, событие A — появление герба при однократном брссании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы.     В случае независимости событий A к B формула (4) примет более простой вид:

(9)

   т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий.     События А1, А2, ..., Аn называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились.     Исходя из этого определения, в случае независимости событий А1, А2, ..., Аn между собой в совокупности на основании формулы (7) имеем

Пример 3. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми ?     Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (5). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через А появление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем   

   Но Р(А)=3/10; РA(В)=2/9, поскольку после того, как был вынут первый белый шар, в урне осталось 9 шаров, из которых 2 белых. Следовательно,   

12 – ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА.

Если событие А может произойти только при выполнении одного из событий  , которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле

.

Эта формула называется формулой полной вероятности.

Вновь рассмотрим полную группу несовместных событий  , вероятности появления которых  . Событие А может произойти только вместе с каким-либо из событий  , которые будем называть гипотезами. Тогда по формуле полной вероятности

Если событие А произошло, то это может изменить вероятности гипотез  .

По теореме умножения вероятностей

,

откуда

.

Аналогично, для остальных гипотез

Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез   называются апостериорными вероятностями, тогда как   -априорными вероятностями.

Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через   обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.

Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

13 – ПОВТОРЕНИЕ ИСПЫТАНИЙ. ФОРМУЛА БЕРНУЛЛИ.

Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность   того, что событие A наступит k раз в n независимых испытаниях, равна:  , где  .