
- •І. Елементи лінійної алгебри
- •1.1. Розв’язування систем лінійних алгебраїчних рівнянь методом Гаусса1
- •Приклади розв’язання слр методом Гаусса
- •Дослідження слр за методом Гаусса
- •Розв’язати систему лінійних рівнянь
- •1.2. Визначники другого порядку. Системи лінійних рівнянь з двома невідомими
- •1.4. Мінори. Алгебраїчні доповнення. Теорема про розклад
- •1.5. Теореми заміщення і анулювання
- •Розв’язання
- •Вправи Обчислити визначники згідно з означенням
- •Відповіді
- •1.6. Розв’язування систем трьох лінійних рівнянь за формулами Крамера. Однорідні системи
- •За формулами Крамера розв’язати систему
- •1.7.1. Визначники вищих порядків
- •1.7.2. Обчислення визначників за правилом прямокутника
- •1.8. Матриці. Означення. Види матриць
- •1.9. Лінійні дії над матрицями
- •1.10. Множення матриць
- •1.11. Визначник добутку матриць
- •1.12. Обернена матриця.
- •Приклади для самостійного розв’язання
- •1.13. Розв’язування систем лінійних рівнянь матричним способом
- •Приклад 2. Розв’язати матричним способом систему
- •1.14.Ранг матриці
- •Знайти ранг матриць
1.11. Визначник добутку матриць
Визначник
квадратної матриці
позначають
 (скорочення від латинської назви
детермінант), або |
|.
Наприклад, якщо
(скорочення від латинської назви
детермінант), або |
|.
Наприклад, якщо
 то
то
 .
.
Теорема. Визначник добутку двох квадратних матриць -го порядку дорівнює добуткові їх визначників, тобто
 ,
або
,
або
 .
(1)
.
(1)
Рівність перевіримо для матриць другого порядку.


Приклад. Перевірити рівність (1) для таких матриць

Розв’язання. Обчислимо спочатку визначники заданих матриць та добуток їх
 ;
;
 ,
,
 .
.
Знайдемо тепер добуток матриць і і теж обчислимо їх визначник

 .
.
 .
.
Отже,
 .
.
Приклади. Знайти визначники матриць:
1.
. 2
. 3.
 .
.
4.
.
5.
. 6. .
.
Для
поданих матриць
 знайти
їх добуток
та обчислити визначники. Результат
перевірити за допомогою теореми.
знайти
їх добуток
та обчислити визначники. Результат
перевірити за допомогою теореми.


Відповіді.
1. -1. 2. 343. 3.
 .
4. 1. 5.
.
4. 1. 5.
 .
6.
.
6.
 .
.
7. 6,-6,-36. 8. -6, -33, 198.
1.12. Обернена матриця.
Поняття оберненої матриці розглянемо на прикладі квадратної матриці третього порядку, яке по аналогії можна буде узагальнити для матриць довільного порядку. Нехай
 .
.
Означення
1.
Матриця
називається неособливою
(невиродженою),
якщо її визначник відмінний від нуля,
тобто
 .
.
Якщо
ж
 ,
то матриця називається особливою
(виродженою).
,
то матриця називається особливою
(виродженою).
Означення
2.
Квадратна
матриця
 називається оберненою
до матри ці
,
якщо виконується рівність
називається оберненою
до матри ці
,
якщо виконується рівність
 (1)
(1)
тобто добуток цих матриць дорівнює одиничній матриці .
Теорема. Якщо матриця - неособлива ( ), то ця умова є необхідною і достатньою для існування оберненої матриці .
Доведемо
необхідність.
Нехай матриця
має обернену
,
тобто
 .
За теоремою про визначник добутку двох
матриць маємо
.
За теоремою про визначник добутку двох
матриць маємо
 ,
бо
,
бо
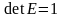 . (2)
. (2)
Тому
рівність (2) можлива тільки тоді, коли
 і
.
і
.
Достатність.
Нехай визначник матриці
відмінний від нуля, тобто
.
Скорочено позначимо
 .
Покажемо, як знайти обернену матрицю.
.
Покажемо, як знайти обернену матрицю.
Для
кожного з елементів
 матриці
знайдемо відповідні їм алгебраїчні
доповнення
матриці
знайдемо відповідні їм алгебраїчні
доповнення
 :
:
 ,
розмістивши їх у вигляді нової матриці
,
розмістивши їх у вигляді нової матриці
 відповідно розташуванню елементів
в
.
Отримаємо
відповідно розташуванню елементів
в
.
Отримаємо
 (3)
(3)
(див., розв’язаний в 1.5 приклад, де отримано матрицю із алгебраїчних доповнень разом з перевіркою вірності їх значень). Протранспонуємо матрицю , замінивши рядки стовпцями, отримаємо формулу оберненої матриці
 . (4)
. (4)
За
допомогою теорем про розклад та анулювання
для визначників третього порядку неважко
перевірити, що
 .
.
Приклад 1. Знайти обернену матрицю до матриці
 .
.
Розв’язання здійснимо у такій послідовності
1) Обчислимо визначник матриці
 .
.
Оскільки , то існує обернена матриця.
2)Знаходимо алгебраїчні доповнення елементів матриці
 ;
; ;
;
 ;
; ;
; ;
; ;
;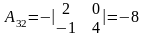 ;
; .
.
3) Записуємо нову матрицю за формулою (3)
 .
.
4) За формулою (4) отримуємо обернену матрицю
 .
.
5) перевіримо, що ,



Приклад 2. Знайти матрицю, обернену до матриці
 .
.
Розв’язання.
1)
 .
.
2)
 ;
;  ;
;
 ;
;  .
.
3)
 .
.
4)
 .
.
5)

 .
.
Приклади для самостійного розв’язання
Знайти обернені матриці для матриць:
1.
 .
2.
.
2.
 .
3.
.
3.
 .
.
4.
 . 5.
. 5.
 .
6.
.
6.
 .
.
7.
 .
.
Відповіді:
1.
 . 2.
. 2.
 3.
3.
 .
.
4.
 . .5.
. .5.
 . 6.
. 6.

7.
 .
.
