4. Комплексный коэффициент передачи,

АЧХ и ФЧХ цифрового фильтра

Комплексным коэффициентом передачи фильтра называется отношение комплексной амплитуды выходного сигнала фильтра y_n к комплексной амплитуде входного синусоидального сигнала x_n

.

Коэффициентом передачи фильтра называется модуль комплексного коэффициента передачи

Частотной характеристикой цифрового фильтра называется зависимость комплексного коэффициента передачи фильтра от частоты.

Амплитудно-частотной характеристикой (АЧХ) называется зависимость модуля комплексного коэффициента передачи от частоты

.

Фазочастотной характеристикой (ФЧХ) называется зависимость аргумента комплексного коэффициента передачи фильтра от частоты.

.

Для нахождения комплексного коэффициента передачи нужно в выражении для системной функции H(z) заменить z на , где f - текущая частота, F_Д – частота дискретизации, T_Д = 1 / F_Д – интервал дискретизации, ω = 2πf.

Задача №4.1

На рисунке 4.1 приведены временные диаграммы входного и выходного сигналов фильтра. Начертите графики АЧХ и ФЧХ фильтра в интервале .

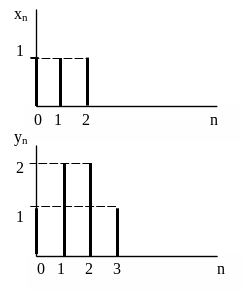
Рисунок 4.1 – Временные диаграммы входного x_n и

выходного y_n сигналов фильтра

Решение задачи №4.1

1. Определим Z- преобразование входного сигнала

2. Определим Z- преобразование выходного сигнала

3. Определим системную функцию фильтра

4. Найдем комплексный коэффициент передачи фильтра

5. Найдем АЧХ K(θ) и ФЧХ φ(θ) фильтра, обозначив

,

,

,

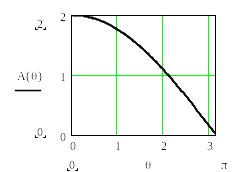
Рисунок 4.2 - Функция A(θ)

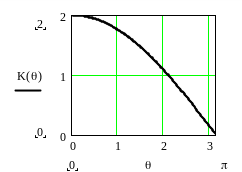
Рисунок 4.3 –АЧХ фильтра

Рисунок 4.4. – ФЧХ фильтра

Задача №4.2

Определите максимальный по абсолютной величине фазовый сдвиг, вносимый цифровым фильтром рисунка 4.5 при А = - 0.5. Постройте график ФЧХ в интервале .

Рисунок 4.5

Решение задачи №4.2

1. Согласно схеме цифрового фильтра разностное уравнение имеет вид:

.

2. Выразим Z-преобразование выходного сигнала фильтра через Z-преобразование входного сигнала

,

,

3. Определим системную функцию фильтра

.

4. Найдем комплексный коэффициент передачи фильтра

.

5. Определим ФЧХ фильтра

.

6. Определим значение , при котором имеет место экстремум ФЧХ.

Поскольку экстремальное значение функции arctg соответствует экстремальному значению её аргумента, определим производную аргумента арктангенса и приравняем её нулю

Откуда

.

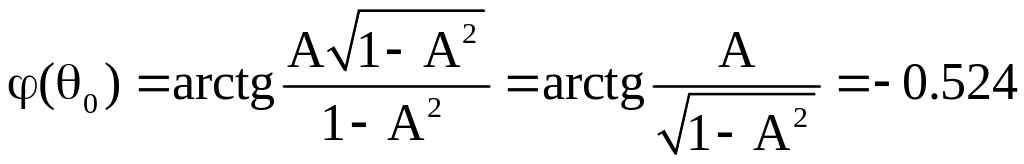График ФЧХ приведен на рисунке 4.6.

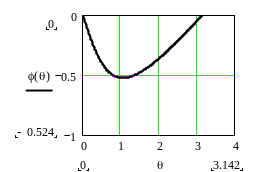
Рисунок 4.6 – ФЧХ фильтра

Задача №4.3

Определите комплексный коэффициент передачи, АЧХ и ФЧХ фильтра, если его системная функция определяется соотношением

.

Константа A = 0.9. Постройте графики АЧХ и ФЧХ в интервале Котельникова.

Решение задачи №4.3

Для нахождения комплексного коэффициента передачи фильтра подставим в выражение системной функции , где - круговая частота, T_Д – интервал дискретизации

Определим АЧХ фильтра

.

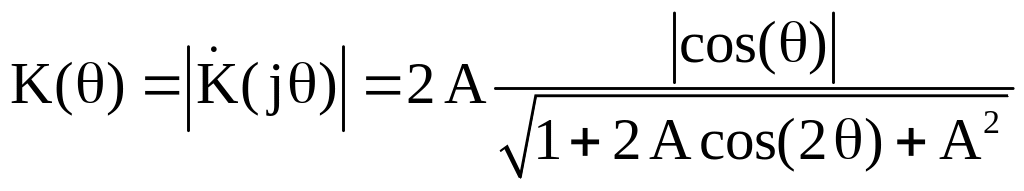Построим график АЧХ при изменении от 0 до с шагом (один градус). Принятый интервал изменения соответствует интервалу частот от 0 до . Внутри этого интервала (кроме частоты ) выполняется теорема Котельникова.

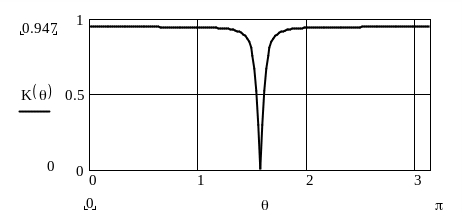
Рисунок 4.7 – АЧХ фильтра

Из графика АЧХ следует, что данный фильтр является режекторным. Его коэффициент передачи равен нулю при , т.е. на частоте, равной половине частоты дискретизации.

Определим ФЧХ фильтра

,

где ,

.

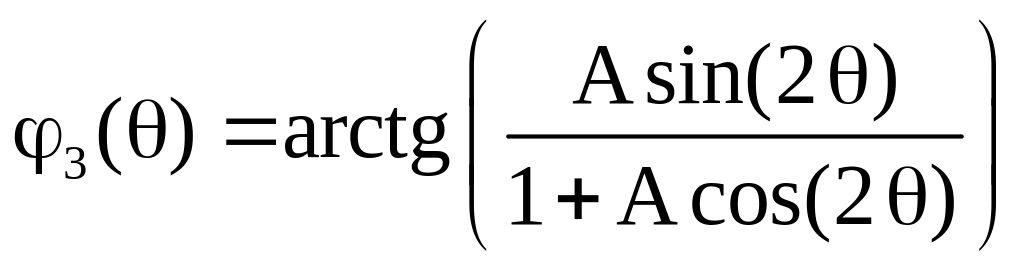На рисунке 4.8 приведены три составляющие ФЧХ, а на рисунке 4.9 результирующая ФЧХ

Рисунок 4.8 – Составляющие ФЧХ фильтра

Рисунок 4.9 – ФЧХ фильтра

Фазочастотные характеристики принято представлять по оси ординат в пределах интервала от до . В рассмотренном случае фазовый сдвиг, вносимый фильтром, не выходит за пределы этого интервала. Поэтому полученный результат следует считать окончательным.

Задача №4.4

Определите АЧХ и ФЧХ цифрового фильтра рисунка 4.10 при B=1. Постойте графики АЧХ и ФЧХ в пределах интервала Котельникова

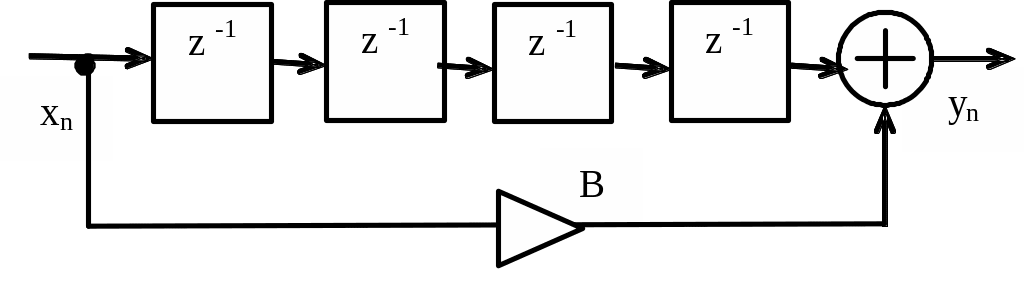
Рисунок 4.10

Решение задачи №4.4

Из схемы рисунка 4.10 следует, что

Выразим Z – преобразование выходного сигнала фильтра через Z – преобразование входного сигнала и определим системную функцию фильтра

Определим комплексный коэффициент передачи фильтра, используя подстановку

где - круговая частота, T_Д – интервал дискретизации

.

Определим АЧХ фильтра

График АЧХ приведен на рисунке 4.11.

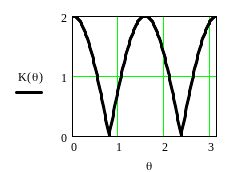
Рисунок 4.11 – АЧХ фильтра

Определим ФЧХ фильтра

где

На рисунке 4.12 приведен график линейной составляющей ФЧХ - функции φ₁(θ), на рисунке 4.13 представлены косинусоида cos(2θ) и составляющая ФЧХ φ₂(θ), а на рисунке 4.14 их сумма φ₀(θ).

Фазочастотные характеристики принято представлять по оси ординат в пределах интервала от до путем прибавления или вычитания 2π m, где m – целое число.

В рассматриваемом случае φ₀(θ) выходит за пределы заданного интервала, поэтому преобразуем полученную характеристику следующим образом:

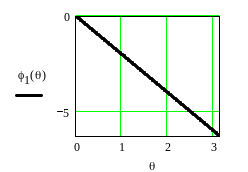
Рисунок 4.12 – Составляющая ФЧХ φ₁(θ)

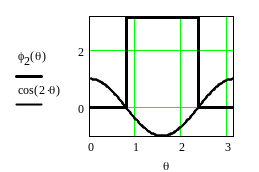
Рисунок 4.13 - Составляющая ФЧХ φ₂(θ)

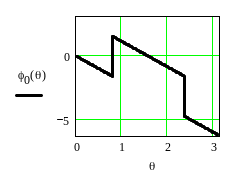
Рисунок 4.14 – ФЧХ φ₂(θ)

Окончательный вариант ФЧХ приведен на рисунке 4.15

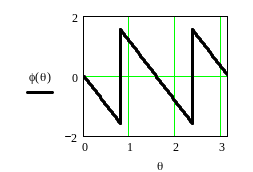
Рисунок 4.15 – ФЧХ фильтра

Задача №4.5

Докажите, что коэффициент передачи K(θ) цифровой цепи рисунка 4.16 не зависит от θ = ωT_Д и равен единице.

Постройте график ФЧХ этой цепи при a = -0.5.

Решение задачи №4.5

Из схемы следует, что

Рисунок 4.16

Используя свойства Z – преобразования, выразим Z – преобразование Y(z) выходного сигнала y_n через Z – преобразование X(z) входного сигнала

Определим системную функцию

Воспользовавшись подстановкой , определим комплексный коэффициент передачи

Определим АЧХ цифровой цепи

Так как модули двух комплексно-сопряженных чисел равны, то в последнем соотношении числитель дроби равен знаменателю.

Так как K(θ) не зависит от частоты, эта цифровая цепь называется всепропускающей.

Определим ФЧХ цифровой цепи

График ФЧХ приведен на рисунке 4.17.

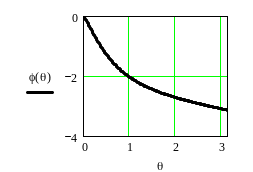
Рисунок 4.17 – ФЧХ всепропускающей цифровой цепи

при a = - 0.5

Задача №4.6

На входе цифрового фильтра рисунка 4.18 действует сигнал

где ωТ_Д = π / 2, X = 0.2.

Чему равна амплитуда выходного сигнала фильтра в установившемся режиме?

Рисунок 4.18

Решение задачи №4.6

Для определения амплитуды выходного сигнала следует найти коэффициент передачи фильтра на частоте входного сигнала, т.е. при θ = π / 2.

Из схемы видно, что

Определим системную функцию фильтр

Определим комплексный коэффициент передачи и его модуль при θ = π / 2

Амплитуда выходного сигнала Y равна произведению амплитуды входного сигнала X = 0.2 на коэффициент передачи фильтра на частоте входного сигнала K=2. Следовательно, Y=0.4.