§. ПризнакИ сравнения сходимости интегралов от знакопостоянных функций. Мажорантный признак.
а). Мажорантный признак.
Пусть
.
Тогда:
*.
Если сходится интеграл
,
то сходится и интеграл
;
*. Если расходится интеграл , то расходится и интеграл .
Пусть
.
Тогда
(из свойств определенного интеграла).
Перейдем к точной верхней границе для
в правой и левой части неравенства
.
▲
б).
Асимптотическая форма мажорантного
признака. Если из двух
неотрицательных функций собственно
интегрируемым по всем замкнутым
промежуткам
и одна ограничивает другую в окрестности
особой точки:
при
,
то
*. Если сходится, то и сходится
*. Если расходится , то и расходится.
Пусть
в окрестности точки
выполнено
.
Тогда
и
ограничена при
.
Значит
.
Значит
сходится
также сходится. ▲
в). Предельная форма мажорантного признака.
Если отношение двух неотрицательных функций, собственно интегрируемых на любом замкнутом промежутке , имеет конечный предел в особой точке, то два интеграла сходятся или расходятся одновременно.
Т.е.
если
,
то из сходимости
сходимость
,
и из расходимости
расходимость
.
Если же
,
то
сходимость сходимости .
г). Асимптотический признак одновременной сходимости – расходимости несобственных интегралов.
и
с
–
одного порядка при
.
Тогда интегралы
и
сходятся или расходятся одновременно.
с
–
одного порядка при
.
▲
д). Предельная форма признака одновременной сходимости – расходимости интегралов.
Если
и
,
тогда
и
сходятся или расходятся одновременно.
Примеры.
1.
.
При
.
Интеграл от мажорирующей функции
сходится, следовательно исходный
интеграл также сходится.
2.
,
а такой интеграл
на
расходится.
3.
.
Вывод
исходный интеграл сходится при
и расходится при
.
4.
.
Вывод
исходный интеграл сходится при
и расходится при
.
5.
.
Особая точка
.
При
и,
следовательно, исходный интеграл
сходится (см. 3).
§. Условная сходимость.
Def: Если – сходится, но - расходится, то называется сходящимся условно.
Пример.
Условно сходящиеся
интегралы существуют. Рассмотрим
.
Особая точка у этого интеграла только
.
Точка
особой точкой не является, т.к.
подынтегральная функция в окрестности
этой точки ограничена.
*. При после интегрирование по частям, получаем .
Интеграл,
стоящий справа сходится, даже абсолютно
т.к.
.
Однако не забывая о том, что абсолютная
сходимость не инвариантна относительно
интегрирования по частям, можем утверждать
только, что исходный интеграл сходится.
*.
Исследуем интеграл
на
на абсолютную сходимость.
.
Первый из интегралов в правой части
неравенства расходится, а второй
сходится. Из этого можно заключить, что
исходный интеграл является сходящимся
но, при этом, не сходится абсолютно.
Следовательно, интеграл
является условно сходящимся интегралом.
§. ПризнакИ Абеля и Дирихле (для функций вида ).
Т.
Интеграл
от произведения
двух функций сходится, в общем случае,
условно, если:
*. Абель: , монотонна и ограничена на ;
*.
Дирихле: Для функции
т.е. интегралы от
по всем промежуткам, вложенным в
ограничены в совокупности (т.е.
имеет ограниченную первообразную) и
монотонно стремится к 0 при
.
Т.к. функция монотонна то
=
.
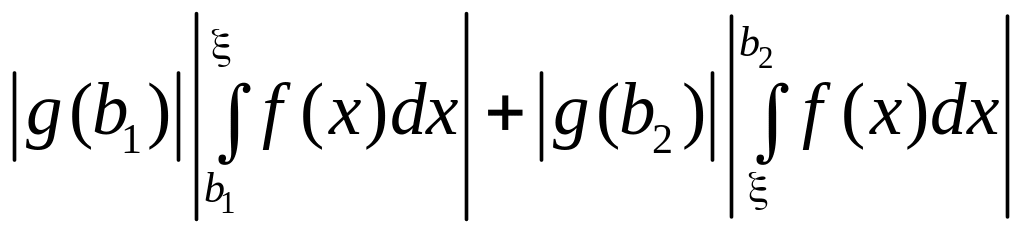Абель:
Т.к.
то
.
И,
следовательно, для
выполнен критерий Коши. Интеграл
сходится.
Дирихле:
и
при
.
Следовательно
.
Интеграл сходится. ▲
Пример:
Исследовать
на абсолютную и условную сходимость
интеграл:
.
Особые точки: и .
1)
Функция
знакопостоянна и
а интеграл от этой функции сходится при
и расходится при
.
2)
Функция
монотонно убывает и стремится к нулю,
а функция
имеет интегралы, ограниченные на
в совокупности.
Т.е.
при
интеграл сходится по Дирихле, вообще
говоря, условно.
3)
интеграл расходится.
4) А абсолютная сходимость?
.
При
интеграл сходится абсолютно.