§. Признак РаАбе.

Последовательность для ряда называется последовательностью Раабе.

Признак Раабе: Если при достаточно больших n выполняется неравенство , то ряд сходится, а в случае ряд расходится.

Предельная форма признака Раабе: Если существует (конечный или нет), то при ряд сходится, а при расходится.

Δ Пусть  .

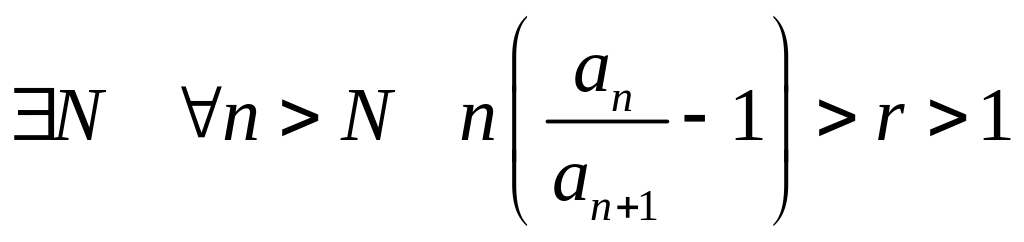
Выберем S, такое, что 1< S < r. Тогда т.к. , то 

и, следовательно, 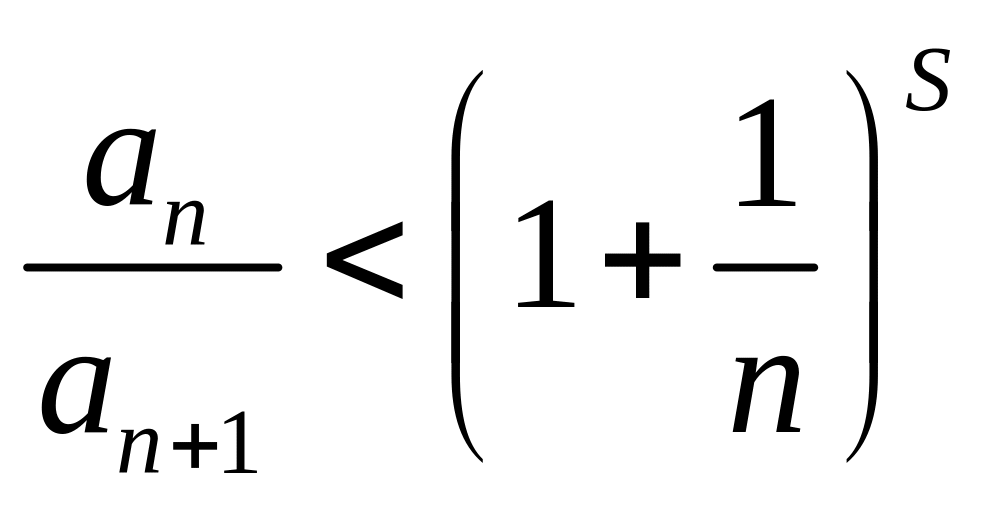. Тогда : из признака Даламбера для сходящегося ряда (при S >1), следует, что 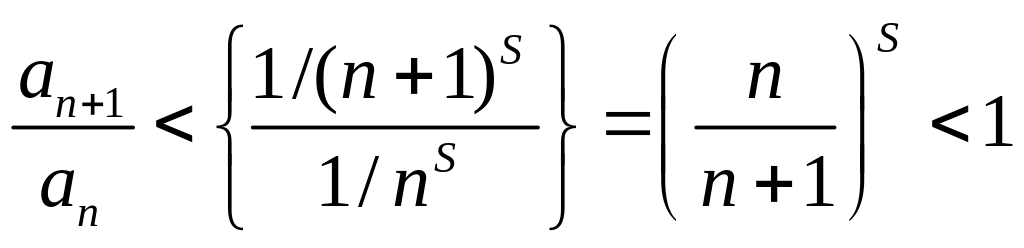. Значит и, по признаку Даламбера, ряд – сходится.

Если  и, так как ряд расходится, то и ряд расходится. ▲

• Для примера рассмотрим ряд: .

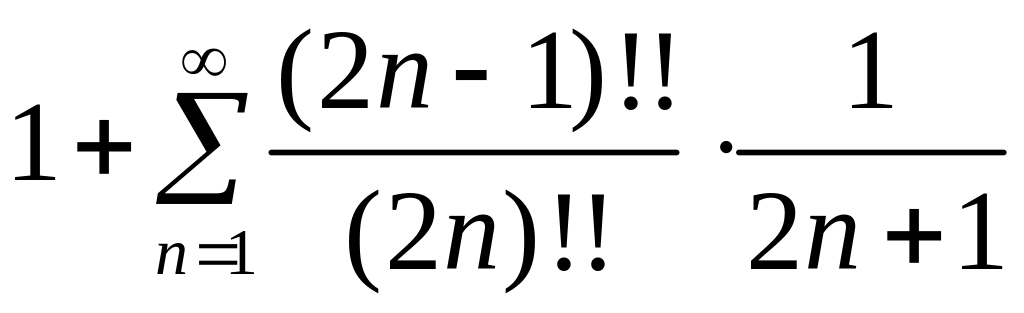Для него: – ряд сходится.

§. Признак Куммера.

Признак Куммера – весьма общий признак. Это скорее не признак, а схема для получения различных, конкретных признаков. Пусть – произвольная последовательность положительных чисел таких, что - расходится. Последовательностью Куммера для ряда назовем последовательность .

Признак Куммера:

Если , то ряд сходится, а если , то ряд - расходится.

Предельная форма признака Куммера: Если , то при ряд сходится, а при ряд расходится.

Δ. Пусть   .

Значит последовательность монотонно убывает и ограничена т. е. имеет предел. Тогда ряд сходится, т. к. его частная сумма: имеет предел.

Но из неравенства следует, что ряд сходится. ▲

Теперь: а). Положим . Тогда:  Для сходимости ряда необходимо, чтобы . Получен признак Даламбера.

б). Положим . Тогда  Для сходимости ряда необходимо, чтобы . Получен признак Раабе.

в). Положим . Тогда: = = . Здесь – последовательность Бертрана, и мы получаем

Признак Бертрана : Если (конечный или нет) и , то при b >1 ряд сходится, а при b <1 ряд расходится.

Из признаков Даламбера, Раабе, Бертрана следует признак Гаусса:

Если для ряда верно, что , где λ, μ – постоянные, а – ограниченная величина, то тогда: ряд сходится если λ > 1 или λ = 1, μ > 1,

ряд расходится если λ < 1 или λ=1 μ 1.

§. Признаки сходимости знакопеременных рядов. А). Признак Лейбница для знакопеременных рядов.

Рассмотрим ряд: , . Если для указанного знакочередующегося ряда и монотонно, то ряд сходится, вообще говоря, условно.

Δ Для ряда рассмотрим четные частные суммы ряда: . Если сгруппировать отдельные слагаемые по два начиная с первого, то получим , а при группировке отдельных слагаемых по два начиная со второго, получим . Таким образом последовательность четных частных сумм возрастающая и ограничена сверху. Тогда .

Рассмотрим нечетные частные суммы того же ряда и, переходя к пределу при , получим, что и, следовательно, т. е. ряд сходится. ▲

Пример: сходится по Лейбницу, а – расходится, ибо это гармонический ряд. Следовательно, исходный ряд сходится условно .

Б). Признаки Абеля и Дирихле.

Изучается сходимость рядов вида . Обозначая = , проделаем следующее преобразование, которое принято называть преобразованием Лапласа.

= = =

= = .

Проделав такое преобразование, запишем:

(*)

Признаки Абеля и Дирихле сходимости рядов вида :

Пусть:

Абеля: Последовательность {b_n} монотонна и ограничена, а ряд сходится.

Дирихле: Последовательность {b_n} монотонно стремится к нулю, а частные суммы ряда ограничены в совокупность.

Тогда: ряд сходится, вообще говоря, условно.

Δ. +

+ . Внизу, на месте индексов, в выражениях написаны оценки, следующие из условий признака Дирихле. Ряд сходится. Признак Дирихле доказан.

Запишем ряд в виде , где , т.к. – монотонна и ограничена, из условий признака Абеля. Тогда сходится по условию, а сходится по Дирихле. Ряд сходится. Признак Абеля доказан. ▲

Интересная особенность Признак Дирихле доказан с помощью преобразования Абеля, а признак Абеля доказан с помощью признака Дирихле.

Пример: а). Исследовать ряд на сходимость: .

Последовательность и монотонна. = =

= = =

= . Тогда , т.е. частные суммы ряда ограничены. Ряд сходится по Дирихле, вообще говоря, условно.

Самое время поставить вопрос о абсолютной сходимости ряда.

Рассмотрим .

Первый из полученных рядов расходится по мажорантному признаку, т.к. . Второй из полученных рядов сходится по Дирихле (аналогично исходному ряду). Таким образом, ряд – расходится. Исходный ряд не сходится абсолютно, но сходится. Следовательно, ряд условно.

б). Исследовать на сходимость ряд .

Прежде всего, обратим внимание на следующее ошибочное рассуждение: Т.к. при , то . По асимптотическому признаку одновременной сходимости – расходимости рядов, ряды с эквивалентными членами сходятся или расходятся одновременно. В предыдущем примере показана сходимость ряда . Следовательно, сходится и ряд . Ошибочность этого рассуждения заключается в том, что асимптотический признак одновременной сходимости –

расходимости рядов применим только к знакопостоянным рядам, а исходный ряд таковым не является.

И, тем не менее, исходный ряд сходится, что легко установить. Ряд сходится, как было установлено в предыдущем примере. А последовательность ограничена и монотонно стремится к единице. Ряд сходится по признаку Абеля.