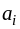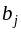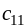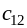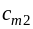- •Математика
- •Санкт-Петербург
- •Содержание
- •Общие положения
- •2. Методические указания к изучению дисциплины
- •3. Методические указания к выполнению контрольной работы
- •Контрольная работа №1
- •Тема 1. Решение матричных уравнений
- •Каждой квадратной матрице ставится в соответствие число
- •Пример1. Найти а-1 , если .
- •Пример2.
- •Тема 2. Решение систем линейных уравнений
- •Контрольные задания
- •Тема 3. Основы дифференциального исчисления
- •Контрольные задания
- •Тема 4. Функции двух переменных
- •Контрольные задания
- •Тема 5. Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования Непосредственное интегрирование
- •Замена переменой в неопределенном интеграле
- •Интегрирование по частям в неопределенном интеграле
- •Интегрирование рациональных дробей
- •Контрольные задания
- •Тема 6. Определенный интеграл
- •Контрольные задания
- •Тема 7. Дифференциальные уравнения
- •Уравнение с разделяющимися переменными
- •Однородное уравнение первого порядка
- •Линейное уравнение первого порядка
- •Контрольные задания
- •Тема 8. Ряды Рассмотрим выражение вида
- •Контрольные задания
- •Контрольная работа №2
- •Тема 1. Случайные события
- •Контрольные задания
- •Тема 2. Случайные величины
- •Контрольные задания
- •Тема 3. Графический метод решения задачи линейного программирования
- •Контрольные задания
- •Тема 4. Симплекс-метод решения задачи линейного программирования
- •Контрольные задания
- •Тема 5. Транспортная задача
- •Контрольные задания
- •5. Требования к выполнению контрольной работы
- •6.1 Основная литература
- •6.1 Дополнительная литература
- •Содержание дисциплины
- •Тема 5.3. Транспортная задача
- •Образец оформления титульного листа контрольной работы
- •Математика
- •Санкт-Петербург
Тема 5. Транспортная задача
Постановка транспортной задачи
Симплекс-метод является универсальным методом решения задач линейного программирования. Однако существуют классы задач, обладающие специфическими свойствами, для которых разработаны более простые методы решения. К такому типу относится задача, получившая название транспортной.
Пусть имеется m
поставщиков
 однородного груза с запасами (мощностями)
однородного груза с запасами (мощностями)
 единиц соответственно. Этот груз
необходимо доставить n
потребителям
единиц соответственно. Этот груз
необходимо доставить n
потребителям
 ,
необходимое количество груза для которых
(емкости) составляет
,
необходимое количество груза для которых
(емкости) составляет
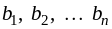 .
Стоимости сij
перевозок единицы груза от i-го
поставщика к j-му
потребителю считаются заданными. Условия
задачи представлены в таблице вида
.
Стоимости сij
перевозок единицы груза от i-го
поставщика к j-му
потребителю считаются заданными. Условия
задачи представлены в таблице вида
|
|
b2 |
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
am |
|
|
|
|
Требуется составить такой план перевозок (т.е. указать количество перевезенного груза от каждого поставщика к каждому потребителю), при котором будут полностью разгружены поставщики и удовлетворены потребители, а транспортные издержки будут минимальны.
Если суммарная мощность поставщиков
равна суммарной емкости потребителей,
т.е.
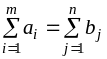 ,
то модель транспортной задачи называется
закрытой, при нарушении этого условия
— открытой.
,
то модель транспортной задачи называется
закрытой, при нарушении этого условия
— открытой.
Закрытая транспортная задача
Рассмотрим задачу закрытого типа.
Обозначим количество груза, перевозимого
от i-го поставщика к j-му потребителю,
через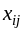 .
.
Составим математическую модель задачи.
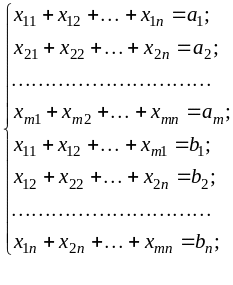 (1)
(1)
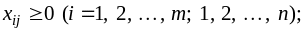 (2)
(2)
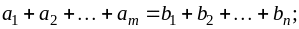 (3)
(3)
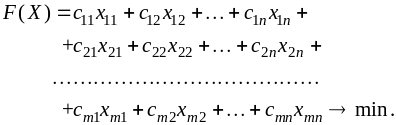 (4)
(4)
Первые m уравнений системы (1)
соответствуют ограничениям по запасам
поставщиков, последние n — ограничениям
потребителей; условие неотрицательности
(2) следует из экономического смысла
неизвестных ; уравнение (2) означает, что
транспортная задача является закрытой.
Целевая функция
 (4)
выражает суммарную стоимость перевозок.
(4)
выражает суммарную стоимость перевозок.
Математически транспортная задача
(1)—(4) ставится следующим образом: среди
множества планов системы линейных
уравнений (1), (3) и неравенств (2) найти
такой план
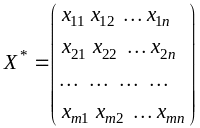 ,
который минимизирует целевую функцию
(4).
,
который минимизирует целевую функцию
(4).
Таким образом, транспортная задача является задачей линейного программирования и может быть решена симплекс-методом, алгоритм которого состоит из трех шагов:
Построение начального плана.
2. Проверка плана на оптимальность. Если план оптимален, то задача решена; в противном случае — переход к п.3.
3. Построение нового плана с меньшей (или равной) стоимостью перевозок.
Специфические особенности системы ограничений транспортной задачи привели к разработке упрощенного метода решения на каждом шаге алгоритма.
Пример 1. Необходимо осуществить перевозки однородного груза от 4-х поставщиков 3-м потребителям, запасы и потребности которых, а также стоимости единичных перевозок заданы таблицей:
|
12 |
9 |
19 |
9 |
10 |
3 |
10 |
8 |
7 |
8 |
12 |
12 |
5 |
5 |
8 |
11 |
2 |
1 |
7 |
Требуется построить такой план перевозок, при котором суммарная стоимость будет наименьшей.
Построение начального плана.
Прежде всего проверим, является ли задача закрытой.
 9+8+12+11=40;
9+8+12+11=40;
 12+9+11=40.
12+9+11=40.
Поскольку
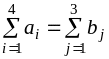 ,
мы имеем дело с закрытой задачей.
,
мы имеем дело с закрытой задачей.
Решение будем строить непосредственно в транспортной таблице 7, которая имеет вид:
Таблица 7.
-
Поставщики
Потребители
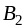
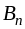
b2
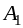

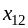
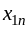
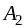




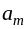

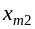

где ai — мощность поставщиков, bj — емкость потребителей, сij —стоимость единичной перевозки, а хij — количество перевозимого груза от Аi поставщика к Bj потребителю, i=1…m, j=1…n.
Начальный план составим методом наименьшей стоимости.
Из всей таблицы выбираем наименьшую
стоимость единичной перевозки сij
и в соответствующую ей клетку
 помещаем наименьшее из чисел
и
.
Тогда или будет полностью исчерпан
запас груза поставщика
помещаем наименьшее из чисел
и
.
Тогда или будет полностью исчерпан
запас груза поставщика
 и в остальных клетках i
-ой строки можно поставить прочерк,
или потребности потребителя
и в остальных клетках i
-ой строки можно поставить прочерк,
или потребности потребителя
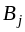 будут полностью удовлетворены и можно
поставить прочерк в оставшихся клетках
j-го столбца.
будут полностью удовлетворены и можно
поставить прочерк в оставшихся клетках
j-го столбца.
Из незаполненных клеток снова выбираем клетку с наименьшей стоимостью, и процесс распределения грузов повторяем, пока все запасы поставщиков не будут распределены, а потребности потребителей полностью удовлетворены. (Если клеток с одинаковой стоимостью несколько, в первую очередь заполняется клетка с наибольшей возможной поставкой.)
В нашем примере наименьшую стоимость
перевозки с42=1 имеет клетка
(4;2). Потребность в грузе потребителя B2
составляет 9, а запас груза поставщика
А4 11 единиц. Наибольшая из возможных
поставок
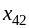 =9
(наименьшее из чисел 11 и 9). Записываем
=9
в таблицу и в оставшихся клетках второго
столбца ставим прочерк, т.к. потребности
B2 будут полностью
удовлетворены. У поставщика А4
остается в запасе 2 единицы груза.
=9
(наименьшее из чисел 11 и 9). Записываем
=9
в таблицу и в оставшихся клетках второго
столбца ставим прочерк, т.к. потребности
B2 будут полностью
удовлетворены. У поставщика А4
остается в запасе 2 единицы груза.
Далее заполняем клетку (4;1) с с41=2. Поставку х42 определим как наименьшее из чисел 12 и 2 (остаток груза А4), х42=2. Потребителю В1 необходимо завезти еще 10 единиц груза, а возможности поставщика А4 будут исчерпаны полностью, в клетке (4;3) ставим прочерк.
Из оставшихся клеток наименьшую стоимость имеет клетка (3;1) с с31=5. Запас груза А3 равен 12, потребность В1 10 единиц, следовательно х31=10. Потребности В1 удовлетворены полностью, в остальных клетках первого столбца ставим прочерки. Оставшиеся у А3 2 единицы поместим в (3;3), т. е. х33=2. Далее вносим в таблицу х23=8, х12=9.
Таблица 8 представляет начальный план задачи Х1. (Полезно проверить, что сумма поставок по столбцам равна соответствующим мощностям потребителей, сумма поставок по строкам — емкостям поставщиков.)
Таблица 8. План Х1.
-
40
40
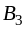
12
9
19
9
10
—
3
—
10
9
8
7
—
8
—
12
8

12
5
10
5
—
8
2

11
2
2
1
9
7
—
Заполненные клетки таблицы соответствуют базисным переменным, а пустые — свободным переменным из системы ограничений (1) (свободные переменные равны нулю). Поскольку система (1) содержит m+n–1 линейно независимых уравнений, то и число базисных переменных будет таким же, (m — число поставщиков, n — число потребителей). План с m+n–1 заполненными (базисными) клетками называется невырожденным, при меньшем числе заполненных клеток — вырожденным. Для того чтобы снять вырождение, необходимо в пустые клетки записать нулевые перевозки, дополнив число базисных переменных до количества m+n–1. Ноль можно поставить только в ту пустую клетку, которая не будет образовывать цикла вместе с уже заполненными клетками.
Циклом называется замкнутая ломаная, вершины которой находятся в клетках, а звенья располагаются вдоль строк и столбцов; в каждой вершине встречаются два звена, одно из которых проходит вдоль строки, а другое — вдоль столбца. Начало и конец ломаной совпадают; она может самопересекаться.
Проверим вырожденность плана нашей задачи: мы имеем 4-х поставщиков и 3-х потребителей, для невырожденного плана число заполненных клеток должно составлять 4+3–1=6. У нас 6 заполненных клеток, следовательно, план невырожденный.
Подсчитаем суммарную стоимость перевозок плана Х1:
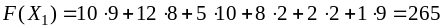 и делаем следующий шаг.
и делаем следующий шаг.
2. Проверка плана на оптимальность.
При проверке плана на оптимальность воспользуемся методом потенциалов.
Каждому поставщику
и потребителю
поставим в соответствие некоторые числа
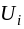 и
и
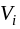 ,
называемые потенциалами, таким
образом, чтобы для всех заполненных
(базисных) клеток выполнялось равенство:
,
называемые потенциалами, таким
образом, чтобы для всех заполненных
(базисных) клеток выполнялось равенство:
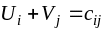 ,
(i=1, 2,
n; j=1,
2,
m). (5)
,
(i=1, 2,
n; j=1,
2,
m). (5)
Количество неизвестных потенциалов
составит m+n,
а уравнений (1) всего m+n–1.
Поэтому один из потенциалов задается
произвольно, после чего остальные
потенциалы из системы уравнений (5)
определяются однозначно. Обычно полагают
 .
.
Для того, чтобы план транспортной задачи был оптимальным, необходимо и достаточно, чтобы для всех пустых (свободных) клеток выполнялось условие
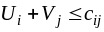 ,
(i=1, 2,
n; j=1,
2,
m). (6)
,
(i=1, 2,
n; j=1,
2,
m). (6)
Если ввести понятие оценки клетки:
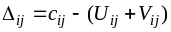 ,
(7)
,
(7)
то условие (6) оптимальности плана можно сформулировать как условие неотрицательности оценок всех пустых клеток:
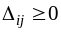 .
(8)
.
(8)
Проверим оптимальность построенного нами начального плана.
По заполненным клеткам определим потенциалы поставщиков Ui и потребителей Vj, которые будем вписывать справа и внизу транспортной таблицы соответственно.
Положим U1 =0. Для заполненных клеток запишем условие (5) и найдем неизвестные потенциалы:
(1;3):
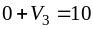 ,
откуда V3=10;
,
откуда V3=10;
(2;3): U2 +10 = 12, U2 = 2;
(3;3): U3 +10 = 8, U3 = –2;
(3;1): –2 + V1= 5, V1 = 7;
(4;1): U4 + 7= 2, U4 = –5;
(4;2): –5+ V2 = 1, V2 =6.
Вычислим оценки пустых клеток по формуле (7):
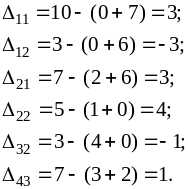
Поскольку среди оценок клеток есть
отрицательные, согласно условию (8)
построенный план
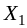 не является оптимальным и может быть
улучшен.
не является оптимальным и может быть
улучшен.
3. Улучшение плана.
Если среди оценок свободных клеток
построенного плана есть хотя бы одна
отрицательная, план может быть улучшен.
Среди пустых клеток с отрицательными
оценками выбираем клетку с наименьшей
величиной
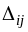 и для нее строим цикл пересчета.
Одна вершина цикла находится в пустой
клетке (i;j),
а остальные — в заполненных. В вершинах
цикла, начиная с пустой клетки,
последовательно расставляем знаки «+»
и «–». Cреди клеток,
помеченных знаком «–» определяется
наименьшее значение перевозки
и для нее строим цикл пересчета.
Одна вершина цикла находится в пустой
клетке (i;j),
а остальные — в заполненных. В вершинах
цикла, начиная с пустой клетки,
последовательно расставляем знаки «+»
и «–». Cреди клеток,
помеченных знаком «–» определяется
наименьшее значение перевозки
 .
Внутри цикла происходит перераспределение
перевозок: в клетки со знаком «+»
добавляется, а из клеток со знаком «–»
вычитается величина
.
Таким образом пустая клетка (i;j)
с наименьшей величиной
получает поставку
;
поставки клеток, не входящих в цикл,
остаются прежними.
.
Внутри цикла происходит перераспределение
перевозок: в клетки со знаком «+»
добавляется, а из клеток со знаком «–»
вычитается величина
.
Таким образом пустая клетка (i;j)
с наименьшей величиной
получает поставку
;
поставки клеток, не входящих в цикл,
остаются прежними.
В результате получаем новый план перевозок. Он может оказаться вырожденным, поэтому нужно следить за тем, чтобы каждый новый план содержал ровно m+n–1 заполненных клеток.
Для нашей задачи среди отрицательных оценок наименьшую оценку имеет клетка (1;2), для нее строим цикл пересчета.
Из клетки (1;2) звено ломаной можно провести только вправо (слева нет заполненной клетки), затем вниз до клетки (3;3) (вершина ломаной не может быть в клетке (2;3), поскольку в этой строке больше нет заполненных клеток). Затем влево до клетки (3;1), далее (4;1), (4;2) и возвращаемся в (4;1). Расставляем чередующиеся знаки «+» и «–» в вершинах ломаной, начиная с вершины в пустой клетке (1;2) (табл. 9).
Таблица 9.
-
10
—
3
—
 +
+10
-
 9
90
7
—
8
—
12
8
2
5
1

 0
-
0
-5
—
8
+ 2
-2
2
2 +
1
9 -
7
—
-5
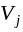
7
6
10
Вычислим = min{9;10;9}=9 — количество груза, перераспределяемое внутри цикла. Величина прибавляется к перевозкам в клетках, помеченных знаком «+», и вычитается из перевозок в клетках, помеченных знаком «–». Изменение величины перевозок происходит только в вершинах цикла, остальные значения хij остаются прежними.
Новый план Х2 должен содержать 6 заполненных клеток, в построенном нами плане их всего 5, т.е. план вырожденный. Так получилось потому, клетки (1;3) и (4;2) одновременно стали пустыми. Чтобы снять вырождение плана, надо в одну из этих клеток дать перевозку, равную нулю, тогда клетка станет базисной. Поставим 0, например, в клетку (1;3), эта нулевая поставка переводит свободную клетку в разряд базисных. План Х2 транспортной задачи представлен в табл.10. (В этой же таблице записаны потенциалы и изображен цикл пересчета, получаемые в дальнейшем).
Таблица 10. План Х2.
-
10
—
3
9
10
0
0
7
— +
8
—
12
- 8
2
5
1 _
5
—
8
+ 11
-2
2
11
1
—
7
—
-5
7
3
10
Изменение значения целевой функции
 можно
вычислить как
=
,
где
—
оценка клетки, для которой построен
цикл,
— количество перемещаемого по циклу
груза.
можно
вычислить как
=
,
где
—
оценка клетки, для которой построен
цикл,
— количество перемещаемого по циклу
груза.
 =
= +
=265+9(-3)=238.
+
=265+9(-3)=238.
Исследуем план Х2 на оптимальность.
Вычислим потенциалы Ui и Vj. Положим U1 =0 и для заполненных клеток (напомним, что клетка (1;3) является заполненной) запишем условие (8.5):
(1;3): , откуда V3=10;
(1;2): 0+V2= 3, V2 = 3;
(2;3): U2+10 = 12, U2= 2;
(3;3): U3 +10= 8, U3= –2;
(3;1): –2+ V1= 5, V1 = 7;
(4;1): U4+7 = 2, V1 = –5;
Сделаем оценки пустых клеток:
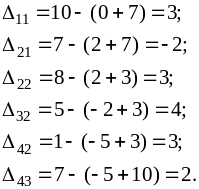
Для плана X2 условие оптимальности (8) не выполнено, т.к. клетка (2;1) получила отрицательную оценку, для нее строим цикл пересчета. Расставляем чередующиеся знаки «+» и «–» в вершинах цикла, начиная с вершины (2;1).
Вычислим = min{8;1}=1. Прибавим это значение к величине перевозок в клетках со знакам «+», вычтем из перевозок в клетках со знакам «–». Получим новый невырожденный план X3, представленный в таблице 11.
Таблица 11. План X3.
|
|
|
|
|
|
10 — |
3 1 |
10 8 |
0 |
|
7 — |
8 8 |
12 — |
2 |
|
5 1 |
5 — |
8 11 |
-2 |
|
2 11 |
2 — |
7 — |
-3 |
|
5 |
3 |
10 |
|
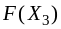 =
+
=238+1(-2)=236.
=
+
=238+1(-2)=236.
Проверим план
 на оптимальность. Найдем потенциалы,
полагая U1
=0:
на оптимальность. Найдем потенциалы,
полагая U1
=0:
(1;3): , откуда V3=10;
(1;2): 0+V2= 3, V2 = 3;
(2;3): U2+10 = 12, U2= 2;
(2;1): 2+ V1= 7, V1 = 5;
(3;3): U3 +10= 8, U3= –2;
(4;1): U4+5 = 2, U4= –3.
Вычислим оценки пустых клеток:
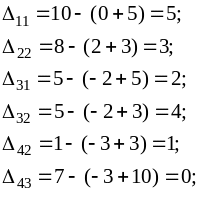
Поскольку все оценки неотрицательны, план X3 является оптимальным.
X3= ,
,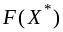 =236.
=236.
Открытая транспортная задача
При нарушении условия
 транспортная
задача называется открытой. Возможны
случаи, когда
транспортная
задача называется открытой. Возможны
случаи, когда
1)
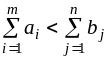 .
Задача сводится к закрытой задаче
введением фиктивного поставщика
.
Задача сводится к закрытой задаче
введением фиктивного поставщика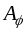 с запасом груза
с запасом груза
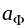 =
= .
Груз, соответствующий поставкам от
.
Груз, соответствующий поставкам от
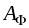 ,
останется недополученным потребителями.
,
останется недополученным потребителями.
2)
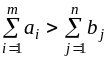 .
Задача сводится к закрытой задаче
введением фиктивного потребителя
.
Задача сводится к закрытой задаче
введением фиктивного потребителя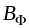 с потребностями в грузе
с потребностями в грузе
 =
=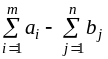 .
Соответствующие ему значения в оптимальном
плане будут означать оставшийся не
отправленным груз поставщиков.
.
Соответствующие ему значения в оптимальном
плане будут означать оставшийся не
отправленным груз поставщиков.
При введении фиктивных поставщиков и потребителей, соответствующие им цены единичных перевозок принимаются равными нулю, если нет других ограничений.
Пример 2. Имеется 3 поставщика и 3 потребителя, запасы грузов и потребности в них, а также цены единичной перевозки указаны в таблице. Требуется составить план перевозок, при котором суммарные транспортные затраты будут минимальными.
|
60 |
60 |
50 |
50 |
3 |
3 |
2 |
70 |
4 |
3 |
2 |
60 |
6 |
7 |
4 |
Прежде всего проверим, является ли поставленная задача закрытой.
 50+70+60=180;
60+60+50=170,
50+70+60=180;
60+60+50=170,
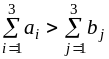 ,следовательно,
это открытая задача второго типа. Введем
фиктивного потребителя
=В4,
потребность в грузе которого примем
равной
=180
–170=10, цены единичных перевозок от
поставщиков фиктивному потребителю
считаем равными нулю, т.е.
,следовательно,
это открытая задача второго типа. Введем
фиктивного потребителя
=В4,
потребность в грузе которого примем
равной
=180
–170=10, цены единичных перевозок от
поставщиков фиктивному потребителю
считаем равными нулю, т.е.
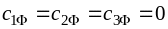 .
Задача становится закрытой, ей
соответствует таблица 12.
.
Задача становится закрытой, ей
соответствует таблица 12.
Составим начальный план методом наименьшей стоимости.
Делаем поставку в клетку (1;3) x13=50, исключаем из рассмотрения первую строку и третий столбец (можно было сделать эту поставку и в (2;4)). Для клетки (2;2) x22=60, во
втором столбце ставим прочерк, у остается 10 единиц груза. Отдаем их , x21=10. У остается потребность 50 единиц, запишем их в (1;1), x31=50. Тогда оставшиеся 10
Таблица 12.
-
180
180

60
60
50
10
50
3
3
2
0
70
4
3
2
0
60
6
7
4
0
единиц у пойдут , x34=10. Начальный план записан в таблице 13.
Таблица 13. План .
-
3
—
 +
+3
—
2
- 50
0
—
0
4
1 0 -
3
60
2
+0
0
—
0
6
50
7
—
4
—
0
10
2
Vj
4
3
2
-2
F(Х1)=
Проверим количество заполненных клеток.
Для нашей задачи их число должно
составлять 3+4–1=6, а в нашем плане только
5, т.е. план вырожден. Поставим 0 в любую
пустую клетку, не образующую цикла с
уже заполненными клетками, например в
(2;3). (Нельзя заполнить нулем клетки
(2;4), т.к. образуется цикл (2;4) (3;4)
(3;1)
(2;1)
(2;4) или (2;3) цикл (3;2)
(3;1)
(2;1)
(2;2)
(3;2))
(3;4)
(3;1)
(2;1)
(2;4) или (2;3) цикл (3;2)
(3;1)
(2;1)
(2;2)
(3;2))
Проверим оптимальность полученного плана.
Определим потенциалы, полагая U1 =0. Для заполненных клеток:
(1;3):
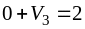 ,
V3=2;
,
V3=2;
(3;2): U2+2= 2, U2 = 0;
(2;2): 0+ V2= 3, V2= 3;
(2;1): 0+ V1=4, V1=4;
(3;1): U3 +4= 6, U3= 2;
(4;1): U4+2 = 0, U4= –2.
Найдем оценки пустых клеток:
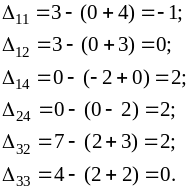
Поскольку среди оценок есть отрицательная, план может быть улучшен.
Для клетки (1;1) строим цикл пересчета, расставляем знаки в вершинах цикла. Определяем =min{10;60}=10, прибавляем это значение к перевозкам в клетках, помеченных знаком «+», вычитаем из перевозок в клетках, имеющих знак «–». Получаем новый план X2, представленный в таблице 14.
Таблица 14. План X2.
-
3
1 0 +
3
—
2
- 40
0
—
0
4
—
3
60
2
10
0
—
0
6
5 0 -
7
—
4
+ —
0
10
3
Vj
3
3
2
-3
= + =620+10(-1)=610.
Проверим оптимальность плана X2.
Для заполненных клеток, считая U1 =0, определяем потенциалы:
(1;1): 0+V1=3, V1=3;
(1;3): , V3=2;
(3;2): U2+2= 2, U2 = 0;
(2;2): 0+ V2= 3, V2= 3;
(3;1): U3 +3= 6, U3= 3;
(4;1): U4+3 = 0, U4= –3.
Для пустых клеток найдем оценки:
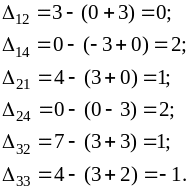
Поскольку одна из оценок отрицательна, план может быть улучшен.
Строим цикл для клетки (3;3). =min{40;50}=40. План представлен в табл.15.
Таблица 15. План .
-
3
50
3
—
2
—
0
—
0
4
—
3
60
2
10
0
—
1
6
10
7
—
4
40
0
10
3
Vj
3
2
1
-3
= + =610+40(-1)=570.
Проверим оптимальность плана X3.
Найдем потенциалы: U1 =0,
(1;1): 0+V1=3, V1=3;
(3;1): U3 +3= 6, U3= 3;
(3;3): 3+ V3= 4, V3= 1;
(3;4): 3+V4=0, V4=3;
(2;3): U2+1=2, U2=1;
(2;1): 1+V2 = 3, V2=2.
Оценки пустых клеток:
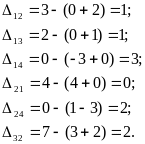
Для плана X3 условие оптимальности (8) выполняется, следовательно, план X3 является оптимальным.
Запишем ответ задачи:
X3=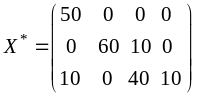 .
.
Поскольку последний столбец оптимального плана соответствует фиктивному потребителю, из окончательного ответа он должен быть исключен. Отброшенное значение x34=10 означает, что 10 единиц груза поставщика А3 останутся нераспределенными. Окончательный ответ —
 ,
F (X*)=570.
,
F (X*)=570.