Изменение координат в суточном движении светил

При рассмотрении данного вопроса примем следующие допущения:

• суточное вращение сферы происходит равномерно;

• оценкой вращения сферы, т. е. времени, относительно меридиана наблюдателя является часовой угол светила t;

• координаты  и  светила не изменяются, а координату t за независимую переменную.

Высота и азимут светила в суточном движении непрерывно изменяются, причем неравномерно. С учетом вышесказанного, требуется получить формулы скорости изменения координат h и A в зависимости от φ, h и А для анализа характера изменения координат.

Эти формулы можно получить аналитическим или графическим методом рассмотренным ниже.

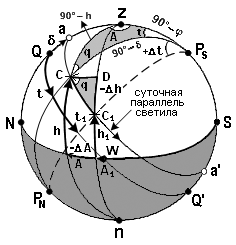
Изменение высоты в суточном движении. Для вывода построим небесную сферу (рис. 10), с суточной параллелью аа светила С.

Рис. 10

На суточной параллели нанесем места (точки) светила С и С₁. Затем, проведя через эти точки меридианы, вертикалы и альмукантарат светила СD, получим малый прямоугольный CDC₁ с элементами:

DC₁ = h – h₁= + h_t;

CD = (A– A₁) cosh = +A_t cosh; (*)

СС₁ = (t– t₁) cos = – t cos; (**)

Примечание. Элементы DC и СС₁ дуги альмукантарата и параллели светила соответственно, величина которых меньше соответствующих им больших кругов в cosh и cos.

Угол DCС₁ = q, как накрест лежащий по отношению к углу q параллактического CZP_S.

Так как CDC₁ малый, то принимая его за плоский, получим формулу скорости изменения высоты

DC₁ = + h_t = СС₁ cosq = – t cos cosq (24)

Заменим аргументы  и q горизонтными координатами, для чего применим формулу синусов к параллактическому ZPC:

sin q sinA

sin(90°– φ) sin(90°– ),

или sinq cos = sinA cosφ

Подставив это выражение в формулу (24), получим окончательно

h_t= – sinA cosφ t (25)

Примечание. При круговом счете азимута h_t= sinA cosφ t.

Анализ общей формулы изменения высоты h_t= h^'_t + h^''_t по А и φ, где h^'_t.– скорость, а h^''_t – ускорение изменения высоты светила.

h^''_t = – cosA cosφ cos cosq sech t²/2

Вывод формулы приведен в литературе [2].

Анализ измерения высоты светила.

На I-ом вертикале (А=90° или 270°) скорость h^'_t = ± cosφ t, а ускорение h^''_t = 0. Следовательно, скорость высоты светила (h_t) будет наибольшая и равномерная.

На меридиане наблюдателя (А=0° или 180°) скорость h^'_t =0, а ускорение наибольшее. Следовательно, скорость около кульминации меняется медленно и неравномерно.

На практике это означает, что около I-го вертикала наиболее точно фиксируется момент времени измерения высоты, т. е. расчетные координаты светила t_м и  будут также более точные. Кроме того, можно усреднять серии высот за больший промежуток времени.

Скорость изменения высоты (h_t) зависит от широты места. При φ= = 90° h_t = 0, т. е. высота светил не меняется, а при φ = 0° и А = 90° h_t= = – t. Следовательно, скорость изменения высоты меняется от 0 до ±t.

Изменение азимута в суточном движении. Для вывода формулы скорости изменения азимута из малого CDC₁ имеем CD = CC₁ cosq;

После подстановки формул (*) и (**) получим

+ A_t cosh = – t cos cosq;

A_t = – cos cosq sech t (26)

Заменим аргументы  и q горизонтными координатами, для чего воспользуемся формулой пяти элементов к углу q и стороне СР_S параллактического треугольника:

cosq sin(90°– ) = sin(90°– h) cos(90°– φ) – cos(90°– h) sin(90°– φ) cosA

или cosq cos = cosh sin φ – sinh cosφ cos A

Заменив в формуле (26) сочетание cosq cos и разделим на cosh, получим окончательную формулу скорости изменения азимута

A_t = – ( sinφ – tgh cosA cosφ) t. (27)

Анализ формулы изменения азимута.

На I-ом вертикале (А=90° или 270°) второе слагаемое равно нулю и азимут изменяется медленно. На меридиане наблюдателя (А = 0° или 180°) скорость, с учетом наибольшего значения сомножителя tgH , изменяется быстро. Практическое применение этого вывода заключается в получении наибольшей разности азимутов за небольшой промежуток времени, который возникает в задаче определения места судна по одному ориентиру, например Солнца.

Скорость изменения азимута (А_t) зависит от широты места и особенно от высоты светила.

П

(28)

ри φ = 90° получим A_t = – t.

При φ = 0° получим A_t = tgh cosA t.

Вывод, на экваторе и в тропиках азимут меняется очень неравномерно от 0 до мгновенного изменения на 180° (при Н= 90°). На полюсах – равномерно А_t = t, т.к. азимут для всех светил равен 180° для северного полюса и 0° для южного полюса.