Calculating Entropy: Microscopic States
Let
represent
the number of possible microscopic states for a given macroscopic
state. (For the four coins shown in Fig. 20.22 the state of four
heads has
,
the state of three heads and one tails has
,
and so on.) Then the entropy
of
a macroscopic state can be shown to be given by
(microscopic
expression for entropy
where
is
the Boltzmann constant. As Eq. (20.22) shows, increasing the number
of possible microscopic states
increases
the entropy
.
What
matters in a thermodynamic process is not the absolute entropy
but
the difference
in
entropy between the initial and final states. Hence an equally valid
and useful definition would be
,
where
is
a constant, since
cancels in any calculation of an entropy difference between two
states. But it's convenient to set this constant equal to zero and
use Eq. (20.22). With this choice, since the smallest possible value
of
is
unity, the smallest possible value of
for
any system is
.
Entropy can never
be
negative.
In
practice, calculating
is a difficult task, so Eq. (20.22) is typically used only to
calculate the absolute entropy
of certain special systems. But we can use this relationship to
calculate differences
in
entropy between one state and another. Consider a system that
undergoes a thermodynamic process that takes it from macroscopic
state 1, for which there are
possible microscopic states, to macroscopic state 2, with
associated
microscopic states. The change in entropy in this process is
(20.23)
The difference in entropy between the two macroscopic states depends on the ratio of the numbers of possible microscopic states.
As the following example shows, using Eq. (20.23) to calculate a change in entropy from one macroscopic state to another gives the same results as considering a reversible process connecting those two states and using Eq. (20.19).
Example 20.11
A microscopic calculation of entropy change
Use Eq. (20.23) to calculate the entropy change in the free expansion of n moles of gas at temperature T described in Example 20.8 (Fig. 20.23).
Solution
IDENTIFY: We are asked to calculate the entropy change using the number of microstates in the initial macroscopic state (Fig. 20.23a) and in the final macroscopic state (Fig. 20.23b).
SET UP: When the partition is broken, the velocities of the molecules are unaffected, since no work is done. But each molecule now has twice as much volume in which it can move and hence has twice the number of possible positions. This is all we need to calculate the entropy change using Eq. (20.23).
EXECUTE:
Let
be
the number of microscopic states of the system
as a whole when the gas occupies volume
(Fig.
20.23a). The number
of molecules is
,
and
each molecule has twice as many
possible states after the partition is broken. Hence the number
of
microscopic states when the gas occupies volume
(Fig.
20.23b) is greater by a factor of
;
that
is,
The change in entropy in this process is
Since and , this becomes
Microscopic States and the Second Law
The relationship between entropy and the number of microscopic states gives us new insight into the entropy statement of the second law of thermodynamics, that the entropy of a closed system can never decrease. From Eq. (20.22) this means that a closed system can never spontaneously undergo a process that decreases the number of possible microscopic states.
An
example of such a forbidden process would be if all of the air in
your room spontaneously
moved to one half of the room, leaving a vacuum in the other half.
Such
a "free compression" would be the reverse of the free
expansion of Examples 20.8 and 20.11. This would decrease the
number of possible microscopic states
by a factor of
.
Strictly
speaking, this process is not impossible! The probability
of finding a given molecule in one half of the room is 1/2, so the
probability of
finding all of the molecules in one half of the room at once is
(1/2)N.
(This
is exactly
the same as the probability of having a tossed coin come up heads N
times
in a row.) This probability is not
zero.
But lest you worry about suddenly finding yourself
gasping for breath in the evacuated half of your room, consider that
a typical
room might hold 1000 moles of air, and so N
= 1000NA
= 6.02 X 1026
molecules.
The probability of all the molecules being in the same half of the
room is therefore
Expressed
as a decimal, this number has more than 1026
zeros to the right of the decimal point!
Because the probability of such a "free compression" taking place is so van-ishingly small, it has almost certainly never occurred anywhere in the universe since the beginning of time. We conclude that for all practical purposes the second law of thermodynamics is never violated.
Thermal Conduction
The energy transfer process that is most clearly associated with a temperature difference is thermal conduction. In this process, the transfer can be represented on an atomic scale as an exchange of kinetic energy between microscopic particles - molecules, atoms, and electrons - in which less energetic particles gain energy in collisions with more energetic particles. For example, if you hold one end of a long metal bar and insert the other end into a flame, you will find that the temperature of the metal in your hand soon increases. The energy reaches your hand by means of conduction. We can understand the process of conduction by examining what is happening to the microscopic particles in the metal. Initially, before the rod is inserted into the flame, the microscopic particles are vibrating about their equilibrium positions. As the flame heats the rod, those particles near the flame begin to vibrate with greater and greater amplitudes. These particles, in turn, collide with their neighbors and transfer some of their energy in the collisions. Slowly, the amplitudes of vibration of metal atoms and electrons farther and farther from the flame increase until, eventually, those in the metal near your hand are affected. This increased vibration represents an increase in the temperature of the metal and of your potentially burned hand.
The rate of thermal conduction depends on the properties of the substance being heated. For example, it is possible to hold a piece of asbestos in a flame indefinitely. This implies that very little energy is conducted through the asbestos. In general, metals are good thermal conductors, and materials such as asbestos, cork, paper, and fiberglass are poor conductors. Gases also are poor conductors because the separation distance between the particles is so great. Metals are good thermal conductors because they contain large numbers of electrons that are relatively free to move through the metal and so can transport energy over large distances. Thus, in a good conductor, such as copper, conduction takes place both by means of the vibration of atoms and by means of the motion of free electrons.
|
Conduction
occurs only if there is a difference in temperature between two parts
of the conducting medium. Consider a slab of material of thickness Ax
and cross-sectional area A.
One
face of the slab is at a temperature 7j, and the other face is at a
temperature T2
> T1
(Fig.
20.9). Experimentally, it is found that the energy Q
transferred
in a time
flows
from the hotter face to the colder one. The rate
at
which this energy flows is found to be proportional to the
cross-sectional area and the temperature difference
and
inversely proportional to the thickness:
It
is convenient to use the symbol for power
to represent the rate
of
energy
transfer:
.
Note that
has
units of watts when
is in joules and A t
is
in Seconds. For a slab of infinitesimal thickness dx
and
temperature difference dT,
we
can write the law
of thermal conduction
as
where
the proportionality constant k
is
the thermal
conductivity
of
the material and |
is
the temperature
gradient
(the
variation of temperature with position);
|
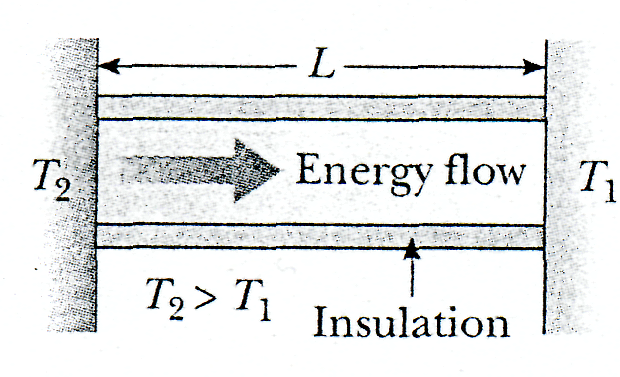
Suppose that a long, uniform rod of length L is thermally insulated so that energy cannot escape by heat from its surface except at the ends, as shown in Figure 20.10. One end is in thermal contact with an energy reservoir at temperature T1, and the other end is in thermal contact with a reservoir at temperature T2 > T1. "When a steady state has been reached, the temperature at each point along the rod is constant in time. In this case if we assume that k is not a function of temperature, the temperature gradient is the same everywhere along the rod and is
Substances that are good thermal conductors have large thermal conductivity values, whereas good thermal insulators have low thermal conductivity values. Metals are generally better thermal conductors than nonmetals are.
Exercises and Problems
Avogadro’s number
How many moles are there in a glass of water (0.2 kg)? How many molecules?
b)How does this distance compare with the diameter of a molecule?
Which has more atoms, a kilogram of a hydrogen, or a kilogram of lead?
Find the mass in kilograms of 7.50 x 1024 atoms of arsenic, which has a molar mass of 74.9 g/mol.
Gold has a molar mass of 197 g/mol. (a) How many moles of gold are in a 2.50 g sample of pure gold? (b) How many atoms are in the sample?
If the water molecules in 1.00 g of water were distributed uniformly over the surface of Earth, how many such molecules would there be on 1.00 cm" of the surface?