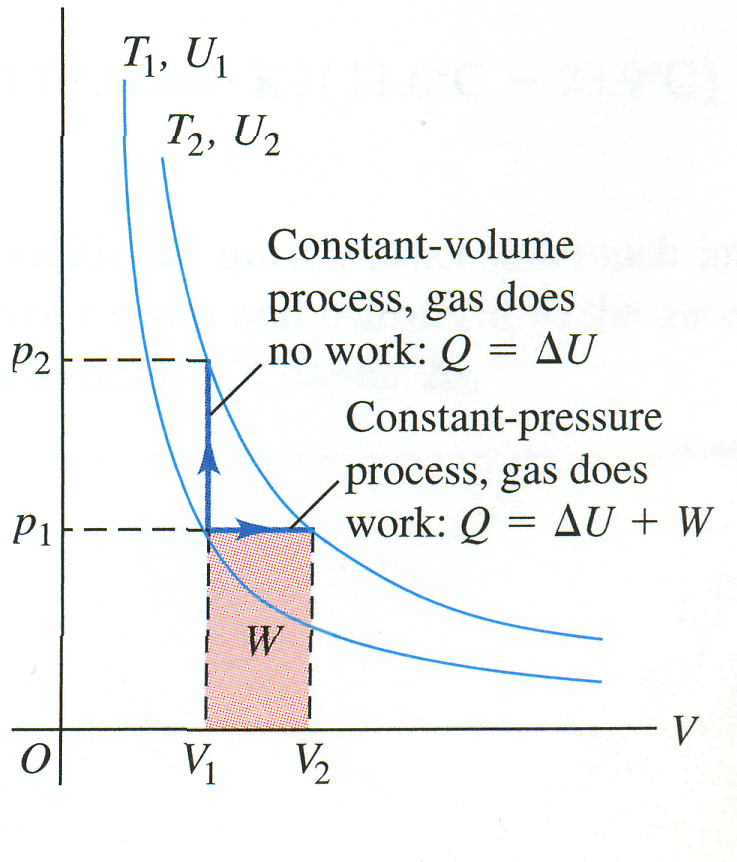
19.7 Heat Capacities of an Ideal Gas

We defined specific heat and molar heat capacity. The specific heat or molar heat capacity of a substance depends on the conditions under which the heat is added. It is usually easiest to measure the heat capacity of a gas in a closed container under constant-volume conditions. The corresponding heat capacity is the molar heat capacity at constant volume, denoted by . Heat capacity measurements for solids and liquids are usually carried out in the atmosphere under constant atmospheric pressure, and we call the corresponding heat capacity the molar heat capacity at constant pressure, . If neither nor is constant, we have an infinite number of possible heat capacities.

Let's consider and for an ideal gas. To measure , we raise the temperature of an ideal gas in a rigid container with constant volume, neglecting its thermal expansion (Fig. 11a).

Fig. 11 a

To measure , we let the gas expand just enough to keep the pressure constant as the temperature rises (Fig. 11b).

Why should these two molar heat capacities be different? The answer lies in the first law of thermodynamics. In a constant-volume temperature increase, the system does no work, and the change in internal energy equals

Fig. 11b

the heat added . In a constant-pressure temperature increase it does an amount of work W. According to the first law,

.

For a given temperature increase, the internal energy change of an ideal gas has the same value no matter what the process (remember that the internal energy of an ideal gas depends only on temperature, not on pressure or volume). Hence the heat input for a constant-pressure process must be greater than that for a constant-volume process because additional energy must be supplied to account for the work W done during the expansion. So is greater than for an ideal gas. For air, is 40% greater than .

For a very few substances (one of which is water between 0°C and 4°C) the volume decreases during heating. In this case, W is negative, the heat input is less than in the constant-volume case, and is less than .

Relating and for an Ideal Gas

We can derive a simple relationship between and for an ideal gas. First consider the constant-volume process. We place n moles of an ideal gas at temperature T in a constant-volume container. We place it in thermal contact with a hotter body; an infinitesimal quantity of heat dQ flows into the gas, and its temperature increases by an infinitesimal amount dT. By the definition of , the molar heat capacity at constant volume, infinitesimal quantity of heat dQ is

(20)

The pressure increases during this process, but the gas does no work ( ) because the volume is constant. The first law in differential form, is . Since , then and Eq. (20) can also be written as

(21)

Now consider a constant-pressure process with the same temperature change dT. We place the same gas in a cylinder with a piston that we can allow to move just enough to maintain constant pressure, as shown in Fig. 11b. Again we bring the system into contact with a hotter body. As heat flows into the gas, it

expands at constant pressure and does work. By the definition of , the molar heat capacity at constant pressure, the amount of heat entering the gas is

(22)

The work dW done by the gas in this constant-pressure process is

We can also express in terms of the temperature change by using the ideal-gas equation of state, . Because is constant, the change in is proportional to the change in :

. (23)

Now we substitute Eqs. (22) and (23) into the first law, . We obtain

(24)

Now here comes the crux of the calculation. The internal energy change for the constant-pressure process is again given by Eq. (21), , even though now the volume is not constant. Why is this so? Recall that one of the special properties of an ideal gas is that its internal energy depends only on temperature. Thus the change in internal energy during any process must be determined only by the temperature change. If Eq. (21) is valid for an ideal gas for one particular kind of process, it must be valid for an ideal gas for every kind of process with the same dT. So we may replace dU in Eq. (24) by :

When we divide each term by the common factor , we get

(25)

As we predicted, the molar heat capacity of an ideal gas at constant pressure is greater than the molar heat capacity at constant volume; the difference is the gas constant R. (Of course, R must be expressed in the same units as and , such as j/mol • K.)

Now we obtain another interesting result/ Let’s return to the Eq. (21):

. (26)

The same from the other hand, can be expressed as

(27)

Therefore, from Eq. (26) and (27) it follows, that

or

. (28)

Substituting (b) into (25) we obtain

. (29)

Ratio of Heat Capacities)

The dimensionless ratio of heat capacities, denoted by is

. (30)

(This is sometimes called the "ratio of specific heats" or "adiabatic factor") For gases, is always greater than and is always greater than unity. This quantity plays an important role in adiabatic processes for an ideal gas, which we will study in the next section.

We can use our kinetic-theory discussion of the molar heat capacity of an ideal gas to predict values of . As an example, an ideal monatomic gas has . From Eq. (25), . So .

This agrees well with values of computed from measured heat capacities. For most diatomic gases near room temperature, , , and

also in good agreement with measured values.

Example Cooling your room A typical dorm room or bedroom contains about 2500 moles of air. Find the change in the internal energy of this much air when it is cooled from 23.9°C to 11.6°C at a constant pressure of 1.00 atm. Treat the air as an ideal gas with = 1.40.

Solution Our target variable is the change in the internal energy of an ideal gas in a constant-pressure process. We are given the number of moles and the temperature change. Your first impulse may be to find and then calculate from ; find the volume change and find the work done by the gas from ; then finally use the first law to find . This would be perfectly correct, but there's a much easier way. For an ideal gas the internal energy change is for every process, whether the volume is constant or not. So all we have to do is find and use this expression for .

EXECUTE: We are given the value of for air, so we use Eqs. (25) and (29) to determine

, J/mol·K

Then

= (2500 mol)(20.79 j/mol • K)(11.6°C - 23.9°C) = -6.39 X 10⁵ J

Heat Capacities of Solids

We can carry out a similar heat-capacity analysis for a crystalline solid. Consider a crystal consisting of N identical atoms (a monatomic solid). Each atom is bound to an equilibrium position by interatomic forces. The elasticity of solid materials shows us that these forces must permit stretching and bending of the bonds. We can think of a crystal as an array of atoms connected by little springs. Each atom can vibrate about its equilibrium position.

Each atom has three degrees of freedom, corresponding to its three components of velocity. According to the equipartition principle, each atom has an average kinetic energy of for each degree of freedom. In addition, each atom has potential energy associated with the elastic deformation. For a simple harmonic oscillator the average kinetic energy of an atom is equal to its average potential energy. In our model of a crystal, each atom is essentially a three-dimensional harmonic oscillator; it can be shown that the equality of average kinetic and potential energies also holds here, provided that the "spring" forces obey Hooke's law.

Thus we expect each atom to have an average kinetic energy and an average potential energy , or an average total energy per atom. If the crystal contains N atoms or n moles, its total energy is

(30)

From this we conclude that the molar heat capacity of a crystal should be

(ideal monatomic solid) (31)

This is the rule of Dulong and Petit, which we encountered as an empirical: Elemental solids all have molar heat capacities of about 25 J/mol • K.

Adiabatic Processes for an ideal Gas

An adiabatic process is a process in which no heat transfer takes place between a system and its surroundings. Zero heat transfer is an idealization, but a process is approximately adiabatic if the system is well insulated or if the process takes place so quickly that there is not enough time for appreciable heat flow to occur.

In an adiabatic process, , so from the first law, . An adiabatic process for an ideal gas is shown in the PV-diagram of Fig. 12. As the gas expands from volume to it does positive work, so its internal energy decreases and its temperature drops. If point a, representing the initial state, lies on an isotherm at temperature , then point b for the final state is on a different isotherm at a lower temperature . For an ideal gas an adiabatic curve (adiabat) at any point is always steeper than the isotherm passing through the same point. For an adiabatic compression from to the situation is reversed and the temperature rises.

The air in the output hoses of air compressors used in gasoline stations, in paint-spraying equipment, and to fill scuba tanks is always warmer than the air entering the compressor; this is because the compression is rapid and hence approximately adiabatic. Adiabatic cooling occurs when you open a bottle of your favorite carbonated beverage. The gas just above the beverage surface expands rapidly in a nearly adiabatic process; the temperature of the gas drops so much that water vapor in the gas condenses, forming a miniature cloud.

CAUTION "Heating" and "cooling" without heat. Keep in mind that when we talk about "adiabatic heating" and "adiabatic cooling," we really mean "raising the temperature" and "lowering the temperature," respectively. In an adiabatic process, the temperature change is due to work done by or on the system; there is no heat flow at all.

Fig. 12

We can derive a relationship between volume and temperature changes for an infinitesimal adiabatic process in an ideal gas. Equation (21) gives the internal energy change for any process for an ideal gas, adiabatic or not, so we have . Also, the work done by the gas during the process is given by . Then, since for an adiabatic process, we have

(32)

To obtain a relationship containing only the volume and temperature , we eliminate using the ideal-gas equation in the form . Substituting this into Eq.(19.19) and rearranging, we get

,

The coefficient can be expressed in terms of . We have

.

Because is always greater than unity for a gas, is always positive. This means that in Eq. (19.20), and always have opposite signs. An adiabatic expansion of an ideal gas ( ) always occurs with a drop in temperature ( ), and an adiabatic compression ( ) always occurs with a rise in temperature ( ); this confirms our earlier prediction.

For finite changes in temperature and volume we integrate Eq. (33), obtaining

, and finally,

(adiabatic process, ideal gas) (34)

Thus for an initial state ( , ) and a final state ( , ),

Or (35)

We can also convert Eq. (34) into a relationship between pressure and volume by eliminating , using the ideal-gas equation in the form Substituting this into Eq. (34), we find

or, because and are constant,

(adiabatic process, ideal gas) (36)

For an initial state (( , )) and a final state ( , ), Eq. (36) becomes

(adiabatic process, ideal gas) (37)

Work done at adiabatic process.

We can also calculate the work done by an ideal gas during an adiabatic process. We know that and for any adiabatic process. For an ideal gas, / If the number of moles and the initial and final temperatures and are known, we have simply

(adiabatic process, ideal gas) (38)

We may also use in this equation to obtain

(39)

We used the result . If the process is an expansion, the temperature drops, is greater than , is greater than , and the work is positive, as we should expect. If the process is a compression, the work is negative.

Throughout this analysis of adiabatic processes we have used the ideal-gas equation of state, which is valid only for equilibrium states. Strictly speaking, our results are valid only for a process that is fast enough to prevent appreciable heat exchange with the surroundings (so that and the process is adiabatic), yet slow enough that the system does not depart very much from thermal and mechanical equilibrium. Even when these conditions are not strictly satisfied, though, Eqs. (35), (37), and (39) give useful approximate results.

The Second Law of Thermodynamics

Many thermodynamic processes proceed naturally in one direction but not the opposite. For example, heat by itself always flows from a hot body to a cooler body, never the reverse. Heat flow from a cool body to a hot body would not violate the first law of thermodynamics; energy would be conserved. But it doesn't happen in nature. Why not? As another example, note that it is easy to convert mechanical energy completely into heat; this happens every time we use a car's brakes to stop it. In the reverse direction, there are plenty of devices that convert heat partially into mechanical energy. (An automobile engine is an example.) But even the cleverest would-be inventors have never succeeded in building a machine that converts heat completely into mechanical energy. Again, why not?

The answer to both of these questions has to do with the directions of thermodynamic processes and is called the second law of thermodynamics. This law places fundamental limitations on the efficiency of an engine or a power plant. It also places limitations on the minimum energy input needed to operate a refrigerator. So the second law is directly relevant for many important practical problems. We can also state the second law in terms of the concept of entropy, a quantitative measure of the degree of disorder or randomness of a system. The idea of entropy helps explain why ink mixed with water never spontaneously unmixes and why we never observe a host of other seemingly possible processes.

Directions of Thermodynamic Processes

Thermodynamic processes that occur in nature are all irreversible processes.These are processes that proceed spontaneously in one direction but not the other. The flow of heat from a hot body to a cooler body is irreversible, as is the free expansion of a gas. Sliding a book across a table converts mechanical energy into heat by friction; this process is irreversible, for no one has ever observed the reverse process (in which a book initially at rest on the table would spontaneously start moving and the table and book would cool down). Our main topic for this chapter is the second law of thermodynamics, which determines the preferred direction for such processes.

Despite this preferred direction for every natural process, we can think of a class of idealized processes that would be reversible. A system that undergoes such an idealized reversible process is always very close to being in thermodynamic equilibrium within itself and with its surroundings. Any change of state that takes place can then be reversed (made to go the other way) by making only an infinitesimal change in the conditions of the system. For example, we can reverse heat flow between two bodies whose temperatures differ only infinitesimally by making only a very small change in one temperature or the other.

Reversible processes are thus equilibrium processes, with the system always in thermodynamic equilibrium. Of course, if a system were truly in thermodynamic equilibrium, no change of state would take place. Heat would not flow into or out of a system with truly uniform temperature throughout, and a system that is truly in mechanical equilibrium would not expand and do work against its surroundings. A reversible process is an idealization that can never be precisely attained in the real world. But by making the temperature gradients and the pressure differences in the substance very small, we can keep the system very close to equilibrium states and make the process nearly reversible. That's why we call a reversible process a quasi-equilibrium process.

By contrast, heat flow with finite temperature difference, free expansion of a gas, and conversion of work to heat by friction are all irreversible processes; no small change in conditions could make any of them go the other way. They are also all nonequilibrium processes, in that the system is not in thermodynamic equilibrium at any point until the end of the process.

In the following sections we will introduce the second law of thermodynamics by considering two broad classes of devices: heat engines, which are partly successful in converting heat into work, and refrigerators, which are partly successful in transporting heat from cooler to hotter bodies.

Heat Engines

The essence of our technological society is the ability to use sources of energy other than muscle power. Sometimes, mechanical energy is directly available; water power and wind power are examples. But most of our energy comes from the burning of fossil fuels (coal, oil, and gas) and from nuclear reactions. They supply energy that is transferred as heat. This is directly useful for heating buildings, for cooking, and for chemical processing, but to operate a machine or propel a vehicle, we need mechanical energy.

Thus it's important to know how to take heat from a source and convert as much of it as possible into mechanical energy or work. This is what happens in gasoline engines in automobiles, jet engines in airplanes, steam turbines in electric power plants, and many other systems. Closely related processes occur in the animal kingdom; food energy is "burned" (that is, carbohydrates combine with oxygen to yield water, carbon dioxide, and energy) and partly converted to mechanical energy as an animal's muscles do work on its surroundings.

Any device that transforms heat partly into work or mechanical energy is called a heat engine. Usually, a quantity of matter inside the engine undergoes inflow and outflow of heat, expansion and compression, and sometimes change of phase. We call this matter the working substance of the engine. In internal-combustion engines, such as those used in automobiles, the working substance is a mixture of air and fuel; in a steam turbine it is water.

The simplest kind of engine to analyze is one in which the working substance undergoes a cyclic process, a sequence of processes that eventually leaves the substance in the same state in which it started. In a steam turbine the water is recycled and used over and over. Internal-combustion engines do not use the same air over and over, but we can still analyze them in terms of cyclic processes that approximate their actual operation.

Hot and Cold Reservoirs

All heat engines absorb heat from a source at a relatively high temperature, perform some mechanical work, and discard or reject some heat at a lower temperature. As far as the engine is concerned, the discarded heat is wasted. In internal-combustion engines the waste heat is that discarded in the hot exhaust gases and the cooling system; in a steam turbine it is the heat that must flow out of the used steam to condense and recycle the water.

When a system is carried through a cyclic process, its initial and final internal energies are equal. For any cyclic process, the first law of thermodynamics requires that

so .

That is, the net heat flowing into the engine in a cyclic process equals the net work done by the engine.

When we analyze heat engines, it helps to think of two bodies with which the working substance of the engine can interact. One of these, called the hot reservoir, represents the heat source; it can give the working substance large amounts of heat at a constant temperature without appreciably changing its own temperature. The other body, called the cold reservoir, can absorb large amounts of discarded heat from the engine at a constant lower temperature . In a steam-turbine system the flames and hot gases in the boiler are the hot reservoir, and the cold water and air used to condense and cool the used steam are the cold reservoir.

We denote the quantities of heat transferred from the hot and cold reservoirs as and , respectively. A quantity of heat is positive when heat is transferred into the working substance and is negative when heat leaves the working substance. Thus in a heat engine, is positive but is negative, representing heat leaving the working substance. This sign convention is consistent with the rules we stated in Section 1; we will continue to use those rules here. Frequently, it clarifies the relationships to state them in terms of the absolute values of the ’s and ’s because absolute values are always positive. When we do this, our notation will show it explicitly.

Energy-Flow Diagrams and Efficiency

We can represent the energy transformations in a heat engine by the energy-flow diagram of Fig. 13. The engine itself is represented by the circle. The amount of heat supplied to the engine by the hot reservoir is proportional to the width of the incoming "pipeline" at the top of the diagram. The width of the outgoing pipeline at the bottom is proportional to the magnitude of the heat rejected in the exhaust. The branch line to the right represents the portion of the heat supplied that the engine converts to mechanical work, .

When an engine repeats the same cycle over and over, and represent the quantities of heat absorbed and rejected by the engine during one cycle; positive, and is negative. The net heat absorbed per cycle is

The useful output of the engine is the net work done by the working substance. From the first law,

(40)

Ideally, we would like to convert all the heat into work; in that case we would have and . Experience shows that this is impossible; there is always some heat wasted, and is never zero. We define the thermal efficiency of an engine, denoted by , as the quotient

. (41)

Fig. 13

The thermal efficiency represents the fraction of that is converted to work. To put it another way, is what you get divided by what you pay for. This is always less than unity. In terms of the flow diagram of Fig. 13, the most efficient engine is one for which the branch pipeline representing the work output is as wide as possible and the exhaust pipeline representing the heat thrown away is as narrow as possible.

When we substitute the two expressions for given by Eq. (40) into Eq. (41), we get the following equivalent expressions for :

(thermal efficiency of an engine) (42)

Note that is a quotient of two energy quantities and thus is a pure number, without units. Of course, we must always express , , and in the same units.

The Second Law of Thermodynamics

Experimental evidence suggests strongly that it is impossible to build a heat engine that converts heat completely to work - that is, an engine with 100% thermal efficiency. This impossibility is the basis of one statement of the second law of thermodynamics, as follows:

It is impossible for any system to undergo a process in which it absorbs heat from a reservoir at a single temperature and converts the heat completely into mechanical work, with the system ending in the same state in which it began.

We will call this the "engine" statement of the second law. (It is also known to physicists as the Kelvin-Planck statement of this law.)

The basis of the second law of thermodynamics is the difference between the nature of internal energy and that of macroscopic mechanical energy. In a moving body the molecules have random motion, but superimposed on this is a coordinated motion of every molecule in the direction of the body's velocity. The kinetic energy associated with this coordinated macroscopic motion is what we call the kinetic energy of the moving body. The kinetic and potential energies associated with the random motion constitute the internal energy.

When a body sliding on a surface comes to rest as a result of friction, the organized motion of the body is converted to random motion of molecules in the body and in the surface. Since we cannot control the motions of individual molecules, we cannot convert this random motion completely back to organized motion. We can convert part of it, and this is what a heat engine does.

If the second law were not true, we could power an automobile or run a power plant by cooling the surrounding air. Neither of these impossibilities violates the first law of thermodynamics. The second law, therefore, is not a deduction from the first but stands by itself as a separate law of nature. The first law denies the possibility of creating or destroying energy; the second law limits the availability of energy and the ways in which it can be used and converted.