Вопрос 22 Экстремумы

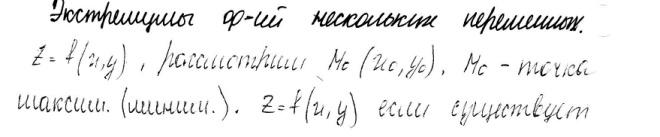
Вопрос 23 Метод наименьших квадратов

Предположим, что есть N-наблюдений, в рез-те происходит замер x,y.Результатом получим: (x1,y1), (x2,y2),…,(xn,yn). Предполагая, что между x и y существует зависимость y=f(x), необходимо найти значение параметров ф-и f, при которых она лучше согласуется с экспериментальными данными. y=f(x)-эмпирическая.

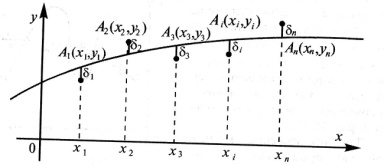
(x;f(x)) ; f(x1)-y1= δ1. Согласно МНК, параметры f(x) следует выбирать так, чтобы сумма кв.ошибок была минимальной.

F(x)=ax+b; F(x)=ax²+bx+c; f(x)=a/x+b. Выбрав одну их них, можно подобрать параметры с помощью МНК:

F(x)=ax+b

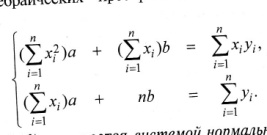
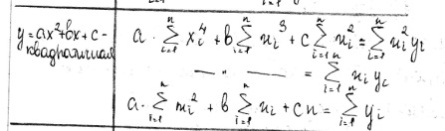
Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

24 Вопрос Неопределенный интеграл, свойства

y=f(x); F(x)-первообразная, если ее производная совпадает с f(x). F(x)=x² F(x)=x³/3. Если y=f(x) и известна F(x), то можно даказать Ф(x)=F(x)+C, где С=const: Ф`(x)=F(x)+C= F`(x)+C`= F`(x)=f(x): Ф(x)-первообразная для f(x)=>если имеется y=f(x), для которой есть F(x), то для этой функции существует целый класс первообразных F(x)+C. Множество F(x)+C – неопределенный интеграл для f(x): ∫f(x)*

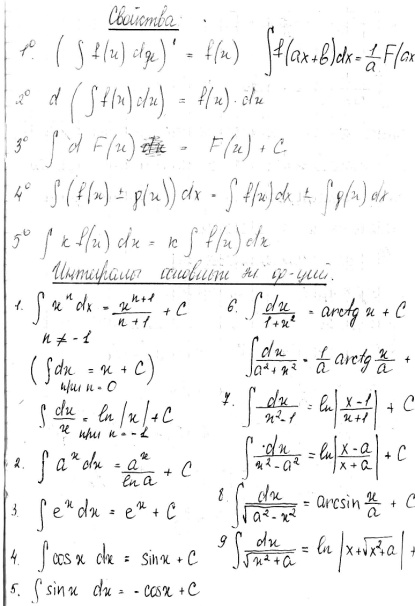
25.Методы интегрирования неопред. Интеграла.

1. Непосредственное интегрирование.

Несомненно, основным методом нахождения первообразной функции является непосредственное интегрирование с использованием таблицы первообразных и свойств неопределенного интеграла. Все другие методы используются лишь для приведения исходного интеграла к табличному виду. Пример.

Найдите множество первообразных функции  . Решение.

Запишем функцию в виде  . Так как интеграл суммы функций равен сумме интегралов, то   Числовой коэффициент можно вынести за знак интеграла: 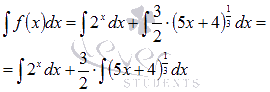  Первый из интегралов приведен к табличному виду, поэтому из таблицы первообразных для показательной функции имеем  .

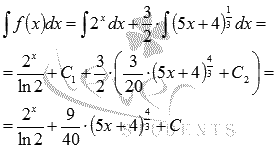Для нахождения второго интеграла   воспользуемся таблицей первообразных для степенной функции   и правилом  То есть,  . Следовательно,    где  . 

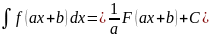
2.Интегрирование по частям

Данный метод основан на правиле дифференц. Произвед. 2-х функций и используется в том случае, когда подынтегральная функция как правило представлена в виде произвед. 2-х функций.

Пусть u(x) и v(x) являются дифференцируемыми функциями. Дифференциал произведения функций u и vопределяется формулой

Проинтегрировав обе части этого выражения, получим

или, переставляя члены,

Это и есть формула интегрирования по частям

.  Основные случаи, когда применяется данный способ интегрирования:    1) подинтегральная функция содержит произведение многочлена от x на показательную функцию от x или произведение многочлена от x на sin(x) илиcos(x), или произведение многочлена от x на ln(x);    2) подинтегральная функция представляет собой одну из обратных тригонометрических функций arcsin(x), arccjs(x) и т.д.;    3) подинтегральная функция есть произведение показательной функции на sin(x) или cos(x).  Пример: необходимо найти интеграл

Положим u = x, dv = sin(x)dx. Тогда du = dx, v = -cos(x). Отсюда