
- •Понятие ф-и и способы ее задания
- •Функции в экономике
- •Вопрос 4. Числовая последовательность и ее пределы.
- •Вопрос 5. Предел функции, основные теоремы о пределах.
- •Вопрос 6. 1ый и 2ой замечательные пределы.
- •7.Бесконечно малые, бесконечно большие величины
- •8.Непрерывность функций. Точки разрыва, их классификация.
- •13. Производная и дифференциал высшего порядка.
- •14. Экономический смысл производной и понятие эластичности.
- •15. Приложение производной.
- •5.Теорема(правило) Лопиталя.
- •Вопрос 22 Экстремумы
- •Вопрос 23 Метод наименьших квадратов
- •24 Вопрос Неопределенный интеграл, свойства
- •25.Методы интегрирования неопред. Интеграла.
- •1. Непосредственное интегрирование.
- •2.Интегрирование по частям
- •3.Метод замены переменной
- •4.Интегрирование рациональных дробей.
- •27.Методы интегрирования определенноно интеграла.
- •28. Несобственные интегралы.
- •29. Дифференциальные уравнения.
- •30. Решение дифференциальных уравнений.
8.Непрерывность функций. Точки разрыва, их классификация.
①Функция y=f(x)- непрерывная в т.x0,если она удовлетвор. 3-м условиям:
1)функция определена в т. x0
2)при x-> x0 функция имеет конечный предел
3)данный предел = значению функции в т. x0 lim f(x)=f(x0) при x-> x0 (*)
Если в (*) существуют односторонние пределы, т.е. lim f(x)=f(x0) при x-> x0+0
и lim f(x)=f(x0) при x-> x0-0,то говорят, что f(x) –непрерывна слева или справа в т.x0
Cв-ва непрерывности функции в данной точке x0 выражаются непрерывностью графика в этой точке.
②т.x0 называется точкой разрыва функции y=f(x), если функция в этой точке не является непрерывной.
Различают несколько типов т. разрыва:
1)Точки разрыва I рода , f(x),- имеет односторонние пределы, но они не равны между собой
2)Точки разрыва II рода.Если хотя бы один из односторонних пределов =∞ или не существует.
Среди точек I рода можно выделить так называемые точки устранимого разрыва: точки, в которых существует предел функции, но он ≠ значению функции в этой точке.
Замечание.
Cв-ва функций непрерывных в точке.
Пусть заданы f(x) и g(x) непрерывные в т. x0, тогда
1)f(x) + g(x)-
f(x) * g(x)- все являются непрерывными в т.x0
f(x) : g(x)-
2)Если y=f(x)- непрерывная в т.x0 и значение f(x0)>0, то существует такая окрестность т.х0, в которой f(x)- явл. положительной.
3)Если y=f(u)-непрерывна в т.u0=ϕ(x), a u=f(x)- непрерывна в т.х0, то y=f(ϕ(x))-непрерывна в т.х0.
Из 3 св-ва =.>,что под знаком сложной функции можно переходить к lim
lim f(ϕ(x))= f (limϕ(x)) при x-> x0
③Функция y=f(x)- непрерывна на промежутке (a,b), если она непрерывна в каждой точке этого промежутка. Можно доказать, что все элементарные функции непрерывны на D(y)
9.Cв-ва функций, непрерывных на отрезке.
1) Если y=f(x)-непрерывна на отрезке [a,b], то она ограничена на нем сверху и снизу,т.е. существуют такие числа M и m,что для всех x€ [a,b], справедливо неравенство m<=f(x)<=M
( I теорема Вейерштрасса)
2)Если y=f(x)-непрерывна на отрезке [a,b], то она достигает на этом отрезке наименьшего значения m, и наибольшего М (II теорема Вейерштрасса)
3)Если y=f(x)-непрерывна на отрезке [a,b] и на концах этого отрезка имеет значения противоположных знаков, то внутри отрезка [a,b] найдется такая точка С, что значения функции в ней будут =0( теорема Больцано-Коши)
Функция y=f(x)-называется равномерно-непрерывной на отрезке [a,b], если для любого, сколь угодно малого ε >0 найдется такое δ>0, δ=δ(ε), что для x1,x2€[a,b] удовлетв. |x1-x2|<ε
Теорема Кантера: Если y=f(x)-непрерывна на отрезке [a,b], то она и равномерно-непрерывна на нем.
10. Понятие производной.









![]()


11.Правила дифференцирования и таблица производных элементарных функций.



![]()

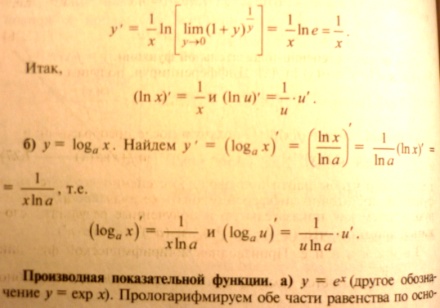

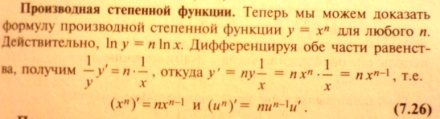

![]()

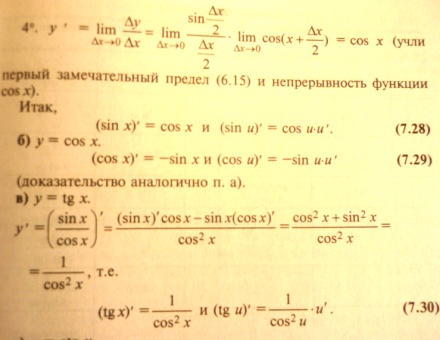



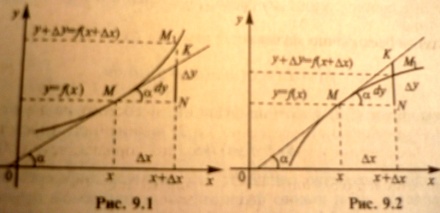
12. Понятие дифференциала функции и его свойства.






13-15 Матан
