У линейного преобразования могут отсутствовать собственные векторы

(пример  вращающиеся плоскости).

П усть теперь матрица А  симметрическая. С ней можно связать квадратную форму

где x  p-мерный вектор-столбец.

С имметрическая матрица А называется положительно определенной, если для любых x0

Симметрическая матрица называется неотрицательно определенной,

если Р:

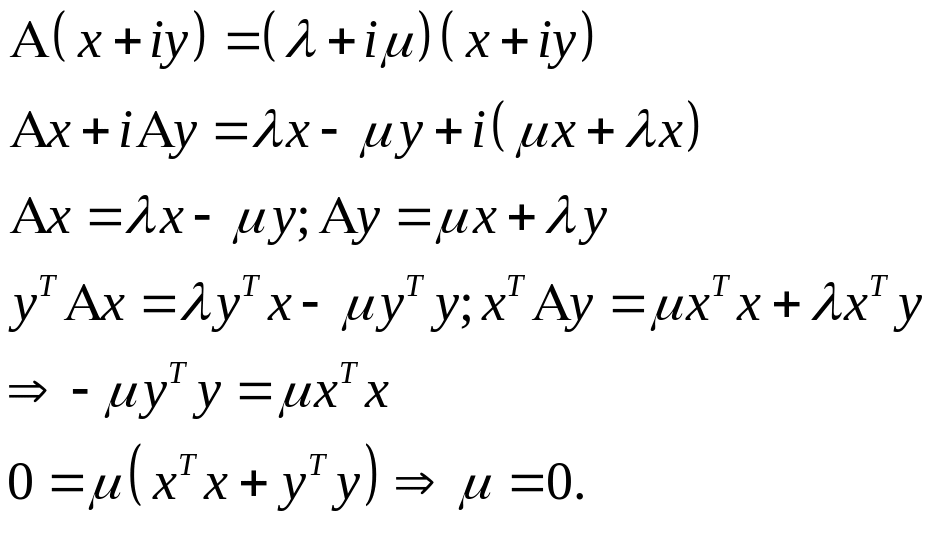1. В се собственные числа симметрической матрицы А  вещественные и соответствующие

им вектора могут быть взяты вещественными :

2. Все собственные числа положительно определенной матрицы А положительны.

Все собственные числа неотрицательно определенной матрицы А неотрицательны.

С ледовательно, характеристические числа положительно определенной матрицы

н еотрицательно определенной

и каждому из них соответствует собственный вектор.

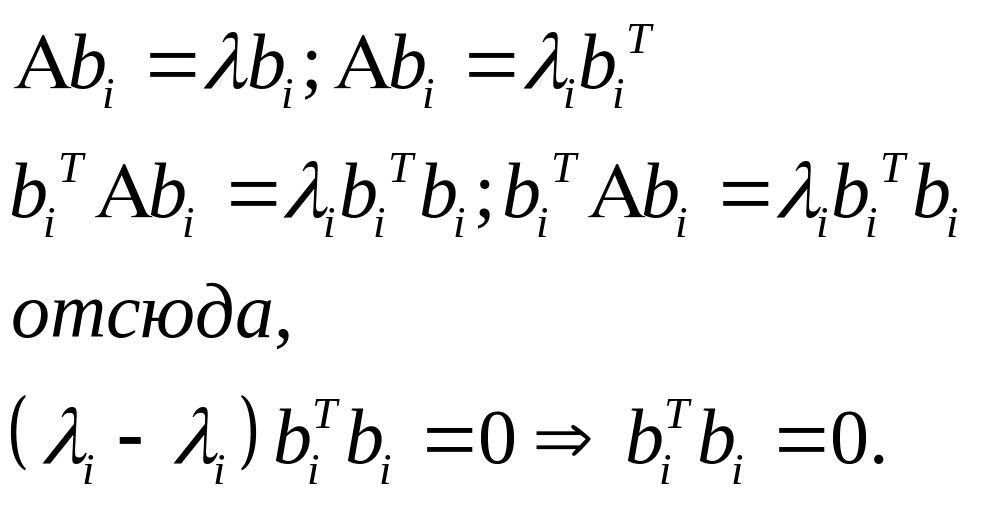1. С обственные векторы b_i и b_j, соответствующие различным собственным числам, ортогональны.

В случае кратных корней размерность пространства решений уравнения (2.10) при ⁽⁰⁾,

где ⁽⁰⁾ корень уравнения (2.11) кратности 2, равно 2.

Все сформулированные и доказанные выше предложения относительно собственных векторов и собственных чисел симметрической матрицы (симметрическое преобразование евклидового пространства) можно получить как следствие двух утверждений.

Утверждение 1: Линейное преобразование  евклидового пространства _n тогда и только тогда будет симметрическим, если в нём существует ортонормированная база, составленная из собственных векторов этого преобразования.

Утверждение 2: Симметрическое линейное преобразование Е_n в любом ортонормированном

базисе задается симметрической матрицей. И обратно, если линейное преобразование в некотором базисе задается симметрической матрицей, то оно является симметрическим.

Вернемся к рассмотрению уравнения (2.11).

Матрица ковариаций , как и всякая матрица ковариаций, является неотрицательно определенной.

Д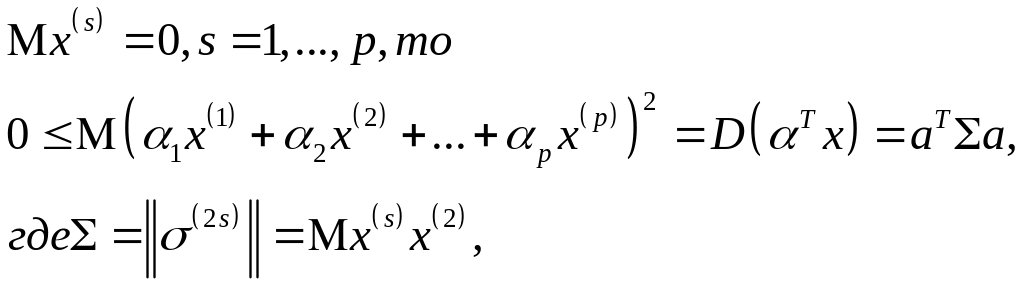 ействительно, поскольку согласно договоренности

д ля любого вектора

Следовательно, собственные значения (характеристические числа) матрицы 

неотрицательны. Расположим их в порядке убывания

                                                                                                                                                                 (2.12)

У множив (2.10) слева на l₁ и учитывая, что

П олучим

и ли после преобразований

О тсюда и из (2.6) следует

В соответствии с определением 1 и соотношением (2.5) для обеспечения максимальной

величины дисперсии нужно выбрать из собственных значений (2.12) матрицы  наибольшее

П одставляя ₁ в систему (2.10) и решая ее относительно

м ы определим компоненты вектора

Таким образом первая главная компонента получается как линейная комбинация , где  собственный вектор матрицы ковариаций , соответствующий наибольшему собственному значению этой матрицы ₁.

В соответствии с определением 2, k-я (k2) главная компонента определяется как норм.

линейная комбинация исходных признаков, имеющая max дисперсию и некоррелированная с предшествующей главной компонентой , где  как можно показать по аналогии с предыдущим собственный вектор матрицы , соответствующий k-му по порядку убывания собственному значению (см. также замечание о кратности корней). При этом .

Таким образом,

                                                                                                                                                                (2.13)

Таким образом, вектор главных компонент , где

п олучается по указанному выше алгоритму в виде произведения ,где строки

матрицы (размерности (р¹р)) ортонормированные р^-мерные вектора, являющиеся собственными векторами матрицы , соответствующими собственным значениям этой матрицы, расположенным в порядке убывания.

При р¹=р матрица (размерности рр) будет ортогональной матрицей и Пу.