
- •22. Дайте определение угловой скорости и углового ускорения вращающегося
- •23Что называется моментом силы, действующей на материальную точку, относительно начала координат?
- •24. Что называется моментом импульса материальной точки относительно начала координат?
- •25. Получите закон изменения момента импульса материальной точки относительно начала координат (уравнение моментов для материальной точки).
- •26. Что называется моментом инерции твердого тела относительно оси вращения?
- •32. Получите закон сохранения момента импульса твердого тела относительно оси _вращения.
- •34. Установите связь между потенциальной энергией и консервативной силой.
- •35. Получите формулу для потенциальной энергии тела в гравитационном поле Земли (вдали от поверхности Земли).
- •36. Какие законы сохранения выполняются при движении тела в центральном гравитационном поле? Получите явные выражения для этих законов сохранения. Какие следствия вытекают из этих законов сохранения?
- •37. Получите формулы для первой и второй космических скоростей тела, движущегося в I рант анионном поле Земли.
- •38. Получите уравнение Мещерского для движения тела с переменной массой Уравнение движения тела с переменной массой
- •39Получите дифференциальное уравнение незатухающих гармонических колебании
- •40По какому закону изменяегся колеблющаяся величина при незатухающих гармонических колебаниях? Приведите график зависимости х(t)
- •40Дайте определение и выведите формулу периода колебаний пружинного маятника.
- •42. Дайтс определение и выведите формулу периода колебаний математического маятника.
- •43. Дайте определение и выведите формулу периода колебаний физического маятника.
- •44. Получите дифференциальное уравнение затухающих гармонических колебаний.
- •45. По какому закону изменяется колеблющаяся величина при затухающих гармонических колебаниях? Приведите график зависимости
- •46. Как определяется логарифмический коэффициент затухания?
- •47. Получите дифференциальное уравнение вынужденных гармонических колебаний.
- •48. От чего зависит амплитуда колебаний при вынужденных гармонических колебаниях? Приведите график зависимости a(q).
- •49. Получите уравнение плоской бегущей волны. Приведите график плоской бегущей волны.
- •50. Получите уравнение стоячей волны. Приведите график стоячей волны.
32. Получите закон сохранения момента импульса твердого тела относительно оси _вращения.
В
случае главной оси вращения при суммарном
моменте внешней силы, действующем на
тело, равном нулю, имеет место закон
сохранения момента импульса твёрдого
тела:
 - закон
сохранения момента импульса твёрдого
тела.
- закон
сохранения момента импульса твёрдого
тела.
Если
суммарный момент внешних сил
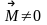 ,
то он совершает работу, которая приводит
к увеличению кинетической энергии
вращающегося твёрдого тела (в этом
случае потенциальная энергия
,
то он совершает работу, которая приводит
к увеличению кинетической энергии
вращающегося твёрдого тела (в этом
случае потенциальная энергия
 ).
).
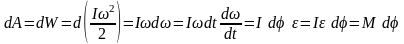
33.
Получите формулу кинетической энергии
вращающегося твердого тела.
Кинетическая энергия
(или энергия
движения) определяется массами и
скоростями рассматриваемых тел.
Рассмотрим материальную точку, движущуюся
под действием силы
.
Работа этой силы увеличивает кинетическую
энергию материальной точки
 .
Вычислим в этом случае малое приращение
(дифференциал) кинетической энергии:
.
Вычислим в этом случае малое приращение
(дифференциал) кинетической энергии:
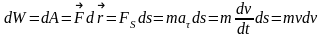 .
.
При
вычислении
 использован
второй закон Ньютона
использован
второй закон Ньютона
 ,
а также
,
а также
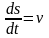 - модуль скорости материальной точки.
Тогда
можно представить в виде:
- модуль скорости материальной точки.
Тогда
можно представить в виде:
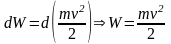 -
-
- кинетическая энергия движущейся материальной точки.
34. Установите связь между потенциальной энергией и консервативной силой.
Если тело в каждой точке пространства подвержено воздействию других тел, то говорят, что это тело находится в поле сил. Так, например, тело вблизи поверхности Земли находится в поле сил тяжести.

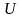 и консервативной силой
,
вычислим элементарную работу по
перемещению материальной точки из точки
1 в близко
расположенную точку 2.
Через точки 1
и 2 проведем
эквипотенциальные поверхности, т.е.
поверхности одинакового потенциала,
которые находятся на расстоянии
и консервативной силой
,
вычислим элементарную работу по
перемещению материальной точки из точки
1 в близко
расположенную точку 2.
Через точки 1
и 2 проведем
эквипотенциальные поверхности, т.е.
поверхности одинакового потенциала,
которые находятся на расстоянии
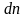 друг от друга. Так как работа совершается
за счет запаса потенциальной энергии,
то потенциальная энергия на поверхности
1 больше чем
на поверхности 2,
а именно, при переходе от поверхности
2 к поверхности
1 она
возрастает на
друг от друга. Так как работа совершается
за счет запаса потенциальной энергии,
то потенциальная энергия на поверхности
1 больше чем
на поверхности 2,
а именно, при переходе от поверхности
2 к поверхности
1 она
возрастает на
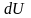 .
Элементарная работа
.
Элементарная работа
 равна
убыли потенциальной энергии:
равна
убыли потенциальной энергии:

Согласно
построению эквипотенциальных поверхностей
сила
всегда перпендикулярны этим поверхностям.
Элементарную работу силы
на перемещении
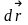 можно
определить и другим способом
можно
определить и другим способом
 .
.
Решая
совместно (1) и (2), находим соотношение
между убылью потенциальной энергии и
силой: .
.
Это
соотношение можно записать в векторной
форме, если ввести векторную величину
– градиент потенциальной энергии
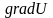 .
По определению это вектор направленный
по нормали к эквипотенциальной поверхности
в сторону возрастания потенциальной
энергии:
.
По определению это вектор направленный
по нормали к эквипотенциальной поверхности
в сторону возрастания потенциальной
энергии:
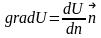 ,
,
где
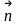 –
единичный вектор нормали. Тогда
–
единичный вектор нормали. Тогда
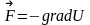 – связь между
консервативной силой и потенциальной
энергией.В
заключении заметим, что градиент
скалярной функции координат
– связь между
консервативной силой и потенциальной
энергией.В
заключении заметим, что градиент
скалярной функции координат
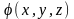 обозначается либо символом
обозначается либо символом
 ,
либо
,
либо ,
где
,
где
 – оператор набла, который имеет вид:
– оператор набла, который имеет вид: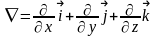 .
.
Тогда
 – градиент
скалярной функции
.
– градиент
скалярной функции
.
35. Получите формулу для потенциальной энергии тела в гравитационном поле Земли (вдали от поверхности Земли).
Потенциальная энергия (или энергия положения тел) определяется действием на тело консервативных сил и зависит только от положения тела.
Мы
видели, что работу силы тяжести
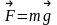 при криволинейном движении материальной
точки
при криволинейном движении материальной
точки
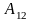 можно представить в виде разности
значений функции
можно представить в виде разности
значений функции
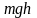 ,
взятых в точке 1
и в точке
2:
,
взятых в точке 1
и в точке
2: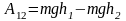 .
.
Оказывается,
что всегда, когда силы консервативны,
работу этих сил на пути 1 2
можно представить в виде:
2
можно представить в виде:
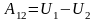 .
.
Функция
 ,
которая
зависит только от положения тела –
называется потенциальной энергией.
,
которая
зависит только от положения тела –
называется потенциальной энергией.
