
- •22. Дайте определение угловой скорости и углового ускорения вращающегося
- •23Что называется моментом силы, действующей на материальную точку, относительно начала координат?
- •24. Что называется моментом импульса материальной точки относительно начала координат?
- •25. Получите закон изменения момента импульса материальной точки относительно начала координат (уравнение моментов для материальной точки).
- •26. Что называется моментом инерции твердого тела относительно оси вращения?
- •32. Получите закон сохранения момента импульса твердого тела относительно оси _вращения.
- •34. Установите связь между потенциальной энергией и консервативной силой.
- •35. Получите формулу для потенциальной энергии тела в гравитационном поле Земли (вдали от поверхности Земли).
- •36. Какие законы сохранения выполняются при движении тела в центральном гравитационном поле? Получите явные выражения для этих законов сохранения. Какие следствия вытекают из этих законов сохранения?
- •37. Получите формулы для первой и второй космических скоростей тела, движущегося в I рант анионном поле Земли.
- •38. Получите уравнение Мещерского для движения тела с переменной массой Уравнение движения тела с переменной массой
- •39Получите дифференциальное уравнение незатухающих гармонических колебании
- •40По какому закону изменяегся колеблющаяся величина при незатухающих гармонических колебаниях? Приведите график зависимости х(t)
- •40Дайте определение и выведите формулу периода колебаний пружинного маятника.
- •42. Дайтс определение и выведите формулу периода колебаний математического маятника.
- •43. Дайте определение и выведите формулу периода колебаний физического маятника.
- •44. Получите дифференциальное уравнение затухающих гармонических колебаний.
- •45. По какому закону изменяется колеблющаяся величина при затухающих гармонических колебаниях? Приведите график зависимости
- •46. Как определяется логарифмический коэффициент затухания?
- •47. Получите дифференциальное уравнение вынужденных гармонических колебаний.
- •48. От чего зависит амплитуда колебаний при вынужденных гармонических колебаниях? Приведите график зависимости a(q).
- •49. Получите уравнение плоской бегущей волны. Приведите график плоской бегущей волны.
- •50. Получите уравнение стоячей волны. Приведите график стоячей волны.
44. Получите дифференциальное уравнение затухающих гармонических колебаний.
45. По какому закону изменяется колеблющаяся величина при затухающих гармонических колебаниях? Приведите график зависимости
46. Как определяется логарифмический коэффициент затухания?
Во
всякой реальной колебательной системе
имеются силы сопротивления, действие
которых приводит к уменьшению энергии
системы. Если убыль энергии не восполняется
за счет работы внешних сил, колебания
будут затухать. В простейшем, и вместе
с тем наиболее часто встречающемся
случае, сила сопротивления
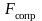 пропорциональна величине скорости:
пропорциональна величине скорости:
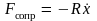 ,
,
где
R
– постоянная, называемая коэффициентом
сопротивления. Знак минус обусловлен
тем, что сила
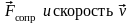 имеют противоположные направления;
следовательно, их проекции на ось х
имеют разные знаки.
имеют противоположные направления;
следовательно, их проекции на ось х
имеют разные знаки.
Второй закон Ньютона при наличии сил сопротивления имеет вид:
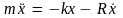
Применив
обозначения: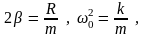
получим:
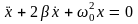 - - дифференциальное
уравнение затухающих гармонических
колебаний.
- - дифференциальное
уравнение затухающих гармонических
колебаний.
Отметим,
что
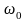 представляет собой ту частоту, с которой
совершались бы свободные колебания
системы в отсутствие сопротивления
среды (при R
= 0). Эту частоту называют собственной
частотой
системы.
представляет собой ту частоту, с которой
совершались бы свободные колебания
системы в отсутствие сопротивления
среды (при R
= 0). Эту частоту называют собственной
частотой
системы.
При
не слишком сильном затухании (при
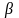 <
)
общее решение уравнения (4) имеет вид:
<
)
общее решение уравнения (4) имеет вид:
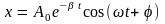 ,
(5)
,
(5)
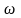 - величина, определяемая формулой
- величина, определяемая формулой
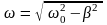 .
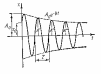
На рисунке дан график функции (5).
Пунктирными линиями показаны пределы,
в которых находится смещение колеблющейся
точки х.
.
На рисунке дан график функции (5).
Пунктирными линиями показаны пределы,
в которых находится смещение колеблющейся
точки х.
В соответствии с видом функции (5) движение системы можно рассматривать как гармоническое колебание частоты с амплитудой, изменяющейся по закону:
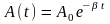 .
.
Верхняя
из пунктирных кривых дает график функции
A(t),
причем
величина
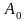 представляет собой амплитуду в начальный
момент времени.
представляет собой амплитуду в начальный
момент времени.
Скорость
затухания колебаний определяется
величиной
 ,
которую называют коэффициентом
затухания.
,
которую называют коэффициентом
затухания.
Период затухания колебаний равен:
 (6)
(6)
При
незначительном сопротивлении среды
(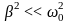 )
период колебаний практически не
изменяется и равен
)
период колебаний практически не
изменяется и равен
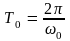 .
Последующие наибольшие отклонения в
какую–либо сторону (например,
.
Последующие наибольшие отклонения в
какую–либо сторону (например,
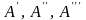 и т.д. на рис.) образуют геометрическую
прогрессию. Действительно, если
и т.д. на рис.) образуют геометрическую
прогрессию. Действительно, если
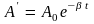 ,
то
,
то
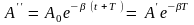 ,
,
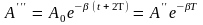 и т.д.
и т.д.
Вообще, отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:
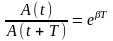
Это соотношение называется декрементом затухания, а его логарифм – логарифмическим декрементом затухания.
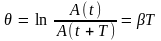 .
(7)
.
(7)
Для
характеристики колебательной системы
обычно используется логарифмический
декремент затухания
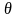 .
Выразив в соответствии с (7)
через
.
Выразив в соответствии с (7)
через
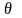 и
и
 ,
можно закон убывания амплитуды со
временем записать в виде:
,
можно закон убывания амплитуды со
временем записать в виде:
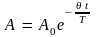 .
.
Для характеристики колебательной системы часто употребляется также величина
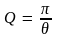 ,
называемая добротностью
колебательной
системы.
,
называемая добротностью
колебательной
системы.
Ранее мы установили, что полная энергия колеблющейся системы пропорциональна квадрату амплитуды. В соответствии с этим энергия системы при затухающих колебаниях убывает со временем по закону:
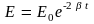 ,
,
где
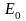 - значение энергии при
- значение энергии при
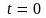 .
.
Из
формулы периода затухающих колебаний
(6) следует, что с ростом коэффициента
затухания период колебаний увеличивается.
При
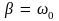 период колебаний обращается в
бесконечность, т.е. движение перестает
быть периодическим.
период колебаний обращается в
бесконечность, т.е. движение перестает
быть периодическим.
При
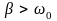 решение дифференциального уравнения
(5) оказывается равным сумме двух
экспонент:
решение дифференциального уравнения
(5) оказывается равным сумме двух
экспонент:
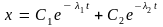 , где
, где
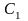 и
и
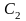 - постоянные, значения которых зависят
от начальных условий (от
- постоянные, значения которых зависят
от начальных условий (от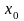 и
и
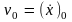 ),
),
 ,
,
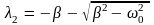 .
.
Д вижение
в этом случае носит апериодический
(непериодический) характер – выведенная
из положения равновесия система
возвращается в положение равновесия,
не совершая колебаний.
вижение
в этом случае носит апериодический
(непериодический) характер – выведенная
из положения равновесия система
возвращается в положение равновесия,
не совершая колебаний.
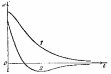
Н

 а
рисунке показано два возможных способа
возвращения системы к положению
равновесия при апериодическом движении.
Каким из этих способов приходит система
к положению равновесия, зависит от
начальных условий.
а
рисунке показано два возможных способа
возвращения системы к положению
равновесия при апериодическом движении.
Каким из этих способов приходит система
к положению равновесия, зависит от
начальных условий.
