
3. Сумма и произведение линейных операторов. Пространство линейных непрерывных операторов
Пусть
А
и В
–
два линейных оператора, действующих из
линейного топологического пространства
Е
в пространство Е1.
Назовем их суммой А+В
оператор С,
ставящий в соответствие элементу
элемент у=Ах+Вх,
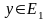 .
.
Можно
проверить, что С=А+В
–
линейный оператор, непрерывный, если А
и В
непрерывны. Область определения DC
оператора С
есть пересечение
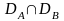 областей определения операторов А
и В.
областей определения операторов А
и В.
Если Е и Е1 – нормированные пространства, а операторы А и В ограничены, то С тоже ограничен, причем
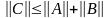 (2)
(2)
Действительно,
для любых х
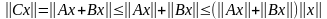 ,
следовательно, выполняется неравенство
(2).
,
следовательно, выполняется неравенство
(2).
Пусть
А
и
В –
линейные операторы, причем А
действует из Е
в Е1,
а В
действует из Е1
в
Е2
. Произведением ВА
операторов А
и В
называется оператор С,
ставящий в соответствие элементу
элемент
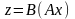 из Е2.
из Е2.
Область определения DC оператора С=ВА состоит из тех х DA , для которых Ах DB. Ясно , что оператор С линеен. Он непрерывен, если А и В непрерывны.
Если А и В – ограниченные операторы, действующие в нормированных пространствах, то и оператор С=ВА – ограничен, причем
 (3)
(3)
Действительно,
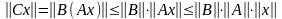 ,
следовательно, выполняется (3).
,
следовательно, выполняется (3).
Сумма и произведение трех и более операторов определяются последовательно. Обе эти операции ассоциативны.
Произведение оператора А на число к (обозначается кА) определяется как оператор, который элементу х ставит в соответствие элемент кАх.
Совокупность Z(E,E1) всех непрерывных линейных операторов, определенных на всем Е и отображающих Е в Е1 ( где Е и Е1 – фиксированные линейные нормированные пространства), образует, по отношению к введенным операциям сложения и умножения на число, линейное пространство. При этом Z(E, E1) – нормированное пространстово (с тем определением нормы оператора, которое было дано выше).
Пусть
Определение. Оператор A,
действующий из линейного пространства
L в линейное пространство M называется
линейным
оператором,
если для любых ![]() из
L и для любого действительного числа ?
справедливо:
из
L и для любого действительного числа ?
справедливо:
![]() и
и ![]() .
.
Действия над операторами. Пусть дан оператор
у = А (х),
причём никакие два разных элемента х и х' не переходят в один и тот же элемент у. Тогда каждому образу у отвечает его единств. прообраз х. Это соответствие называется обратным оператором и обозначают
х = А–1(у).
Построение обратного оператора эквивалентно решению уравнения у = А (х)относительно х (отыскание неизвестного прообраза по данному образу).
Если A1 и А2 — два оператора, отображающих R в R', то их суммой А = A1 + A2 называется оператор, определяемый равенством А (х) = A1(x) + A2(x).Если оператор A1 переводит R в R',а A2 переводит R' в R”, то результат их последовательного применения представляет собой оператор, отображающий R в R”;его называют произведениемA2A1операторов A1 и A2. Если, в частности, рассматриваются операторы, переводящие некоторое линейное пространство в себя, то сумма и произведение двух таких операторов всегда определены. Результат последовательного применения п раз одного и того же оператора А есть n-я степень An этого оператора. Например, n-я степень оператора дифференцирования есть оператор n-kpaтного дифференцирования Dn [f (t)] = f (n)(t). Произведение lА оператора А на число l определяется формулой
(lА)(х) = lА (х).
Оператор Е, переводящий всякий элемент х в самого себя, называется единичным. Нулевым называется оператор О, переводящий каждый элемент в нуль. Очевидно, что при любом А справедливы равенства: AE = EA = А и А+О = О + А = А, далее, если, А–1 существует, то А–1А = AA–1 = Е (следует заметить, что для двух произвольных операторов А и Впроизведения AB и BA,вообще говоря, не равны между собой).
С помощью операций сложения, умножения операторов и умножения операторов на числа можно определить многочлены от линейного оператора, а путём предельного перехода, понимаемого соответствующим образом, — и более сложные функции от оператора. Например, если D — оператор дифференцирования, то eD означает оператор, определяемый формулой
![]() ,
,
имеющий смысл для тех f (t), для которых ряд справа сходится. Для аналитических функций сумма этого ряда равна f (t + 1), т. е. eD — оператор сдвига, переводящий f (t) в f (t + 1).
____________________________________________________________________________
№24
Обратный оператор
Пусть А – линейный оператор, действующий из Е в Е1 , и DA область определения, а RA – область значений этого оператора.
Оператор А называется обратимым, если для любого у RA уравнение Ах=у имеет единственное решение.
Если А обратим, то любому элементу у RA можно поставить в соответствие единственный элемент х DA , являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным к А и обозначается А-1.
Оператор А-1, обратный линейному оператору А, также линеен.
Доказательство.
Достаточно проверить выполнение равенства
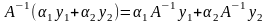 .
.
Положим Ах1=у1 и Ах2=у2, в силу линейности А имеем
 (*)
(*)
По
определению обратного оператора А-1у1=х1
и А-1у2=х2,
умножим оба равенства соответственно
на
 и
и
 :
:
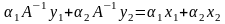 .
.
С
другой стороны из равенства (*) следует
 ,
следовательно,
.
,
следовательно,
.
Теорема доказана.
Матрица обратного оператора
![]() осуществляет
изоморфизм (Ограниченный линейный
оператор
осуществляет
изоморфизм (Ограниченный линейный
оператор ![]() между
нормированными пространствами называется
изоморфизмом, если существует положительное
вещественное число
между
нормированными пространствами называется
изоморфизмом, если существует положительное
вещественное число ![]() такое,
что
такое,
что ![]() для
всех векторов
для
всех векторов ![]() )
) ![]() тогда
тогда ![]() .
.
Возьмём![]() -
базис в L,
-
базис в L, ![]() -
базис в M, тогда:
-
базис в M, тогда:
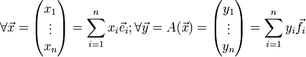
![]() матрица
матрица ![]() осуществляет
действие оператора
осуществляет
действие оператора ![]() -
матрица обратного оператора.
-
матрица обратного оператора.
Условие
обратимости:
-
оператор обратим ![]() оператор
А осуществляет изоморфизм.
оператор
А осуществляет изоморфизм.
Изоморфи́зм — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца,линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.
Объекты,
между которыми существует изоморфизм,
являются в определённом смысле «одинаково
устроенными», они называются изоморфными.
Классическим примером изоморфных систем
могут служить множество ![]() всех
вещественных чисел с определённой на
нём операцией сложения и
множество
всех
вещественных чисел с определённой на
нём операцией сложения и
множество ![]() положительных
вещественных чисел с заданной на нём
операцией умножения. Отображение
положительных
вещественных чисел с заданной на нём
операцией умножения. Отображение ![]() в
этом случае является изоморфизмом.
в
этом случае является изоморфизмом.
____________________________________________________________________________
№25
Выведите формулу преобразования матрицы оператора при переходе к новому базису
Пусть
V – линейное пространство, А – линейный
оператор из L(V,V)
,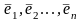 ,
и
,
и
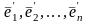 – два базиса в V и
– два базиса в V и
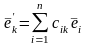 –
формулы перехода от базиса {
–
формулы перехода от базиса {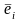 }
к базису {
}
к базису { }.
Обозначим через C=[
}.
Обозначим через C=[ ]
матрицу перехода от базиса к базису.
Отметим, что ранг матрицы С равен n. Пусть
A={
]
матрицу перехода от базиса к базису.
Отметим, что ранг матрицы С равен n. Пусть
A={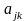 }
и
}
и
 – матрицы оператора А в указанных
базисах.
– матрицы оператора А в указанных
базисах.
Теорема
7.1. Матрицы А и
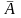 оператора А в базисах {
}
и {
}
связаны соотношением
оператора А в базисах {
}
и {
}
связаны соотношением
 .
.
Доказательство.
При воздействии линейного оператора А
вектор
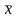 пространства V
переводится в вектор
пространства V
переводится в вектор
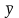 этого пространства, т.е. справедливо
равенство
этого пространства, т.е. справедливо
равенство
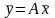 (7.3)
(7.3)
(в старом базисе) и равенство
 (7.4)
(7.4)
(в новом базисе). Так как C – матрица перехода от старого базиса к новому, то
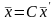 (7.5)
(7.5)
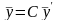 (7.6)
(7.6)
Умножим
равенство (7.5) слева на матрицу A
, получим А
= АC и
с учетом (7.3)
и
с учетом (7.3)
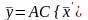 .Заменив
левую часть полученного выражения в
соответствии с (7.6), получим:
.Заменив
левую часть полученного выражения в
соответствии с (7.6), получим: или
или
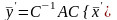 .Сравнивая
найденное выражение с равенством (7.4),
получим доказываемую формулу.
.Сравнивая
найденное выражение с равенством (7.4),
получим доказываемую формулу.
Отсюда следует, что определитель матрицы линейного оператора не зависит от базиса.
____________________________________________________________________________
№26
Определите
понятие собственного вектора, собственного
значения для линейного оператора в
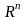 .
Приведите примеры. Покажите, что множество
собственных векторов, отвечающих данному
собственному значению (вместе с нулевым
вектором) образует линейное подпространство
в
.
.
Приведите примеры. Покажите, что множество
собственных векторов, отвечающих данному
собственному значению (вместе с нулевым
вектором) образует линейное подпространство
в
.
Определение.
![]() ,
где x
— это некоторое число, которое называют
собственным вектором оператора А, а
,
где x
— это некоторое число, которое называют
собственным вектором оператора А, а
![]() - собственным значением.
- собственным значением.
![]() -
каждому собственному вектору соответствеут
единственое собственное значение.
-
каждому собственному вектору соответствеут
единственое собственное значение.
 -собств.вектор
линейного оператора
-собств.вектор
линейного оператора
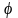 ,если
выполняется
,если
выполняется
 -собственное
значение(число).
-собственное
значение(число).
Множество
L
в
 называется
линейным подпространством пространства
называется
линейным подпространством пространства
 или, короче, подпространством в
, если из того, что два каких-либо вектора
x
и y
принадлежат к L(x,y
L)
автоматически следует, что вектор
или, короче, подпространством в
, если из того, что два каких-либо вектора
x
и y
принадлежат к L(x,y
L)
автоматически следует, что вектор
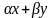 тоже принадлежит к L(
тоже принадлежит к L(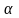 x,
x,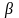 y
L)
, где
,
- числа. Подпространство L
называется m-мерным,
если в нем имеется линейно независимая
система
y
L)
, где
,
- числа. Подпространство L
называется m-мерным,
если в нем имеется линейно независимая
система
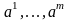 ,
состоящая из m
векторов, и нет системы, состоящей из
m+1
линейно независимых векторов.
,
состоящая из m
векторов, и нет системы, состоящей из
m+1
линейно независимых векторов.
____________________________________________________________________________
№27
Докажите, что собственные векторы , отвечающие различным собственным значениям линейно независимы.
Определение. Система векторов x1, x2, … , xn О X называется линейно зависимой, если существуют числа α1, α2, … , αn О R , не все равные нулю (т.е. α12 + α22 + … + αn2 ≠ 0 ), такие, что
α1x1 + α2x2 + … + αnxn = θ.
Если это равенство выполняется только при α1 = α2 = … = αn = 0 , то система векторов называется линейно независимой.
Доказательство
для n=2.
Пусть - собственные значения, а
- собственные значения, а
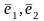 -собственные векторы оператора A
в
-собственные векторы оператора A
в
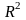 . Покажем, что эти векторы линейны
независимы. Пусть
. Покажем, что эти векторы линейны
независимы. Пусть
![]() и
и
![]()
Отсюда
![]()
![]()
Значит,
![]() . Аналогично,
. Аналогично,
![]() .
.
____________________________________________________________________________
№28
Определение. Ненулевой вектор называется собственным вектором оператора A, если оператор A переводит в коллинеарный ему вектор, то есть . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
____________________________________________________________________________
№29
Пусть в пространстве имеется два базиса: и .
Первый
условимся называть старым базисом,
второй – новым. Каждый из векторов
нового базиса, по Теореме 5.1, можно
линейно выразить через векторы старого
базиса:
 (5.1)
(5.1)
Новые базисные векторы получаются из старых с помощью матрицы

При
этом коэффициенты их разложений по
старым базисным векторам образуют
столбцы этой матрицы. Матрица называется
матрицей перехода от базиса
![]() к базису .
к базису .
![]()
Определитель матрицы не равен нулю, так как в противном случае ее столбцы, а следовательно и векторы , были бы линейно зависимы.
Обратно,
если
![]() ,
то столбцы матрицы линейно независимы,
и следовательно векторы
,
получающиеся из базисных векторов
с помощью матрицы
,
то столбцы матрицы линейно независимы,
и следовательно векторы
,
получающиеся из базисных векторов
с помощью матрицы
![]() ,
линейно независимы и значит образуют
некоторый базис. Таким образом, матрицей
перехода может служить любая квадратная
матрица порядка n с отличным от нуля
определителем.
,
линейно независимы и значит образуют
некоторый базис. Таким образом, матрицей
перехода может служить любая квадратная
матрица порядка n с отличным от нуля
определителем.
Рассмотрим
теперь, как связаны между собой координаты
одного и того же вектора в старом и новом
базисах. Пусть
![]() в старом базисе и
в старом базисе и
![]() - в новом. Подставляя в последнее равенство
вместо
их выражение из (5.1), получим, что
- в новом. Подставляя в последнее равенство
вместо
их выражение из (5.1), получим, что
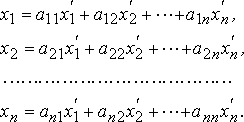
Таким образом, старые координаты вектора получатся из новых его координат с помощью той же матрицы , только коэффициенты соответствующих разложений образуют строки этой матрицы.
____________________________________________________________________________
№30
Скалярное произведение — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора. Для обозначения модуля вектора используются две вертикальные линии слева и справа |AB|.
Модуль вектора (длина вектора) |a| в прямоугольных декартовых координатах равен квадратному корню из суммы квадратов его координат.
Ортогональность — понятие, являющееся обобщением перпендикулярности для линейных пространств с введённым скалярным произведением.
Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу.
Важной особенностью понятия является его привязка к конкретному используемому скалярному произведению: при смене произведения ортогональные элементы могут стать неортогональными, и наоборот.
