
№1
Основные действия над матрицами
Сумма (разность) матриц.
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера.
Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij bij
Обозначение: С = А + В = В + А.
Умножение матрицы на число.
Операция умножения матрицы любого размера на произвольное число сводится к умножению каждого элемента матрицы на это число.
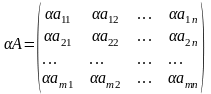
Свойства: (АВ) =А В
А() = А А
Пример: Даны матрицы А =
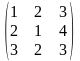 ;
B =
;
B =
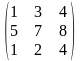 ,
найти 2А + В.
,
найти 2А + В.
2А =
 , 2А
+ В =
, 2А
+ В =
 .
.
Произведение двух матриц.
Замечание: Операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй. В противном случае произведение матриц не определено.
Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
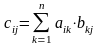
Обозначение: AB = C;
Из приведенного определения видно, что каждый элемент матрицы С равен алгебраической сумме произведений элементов i – той строки матрицы А на соответствующие элементы j – го столбца матрицы В.
Отсюда правило:
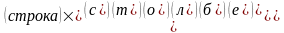
Свойства:
1) Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
АЕ = ЕА = А
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа верно соотношение:
(AB) = (A)B = A(B).
____________________________________________________________________________
№2
Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
Транспонирование
В линейной алгебре матрица считается матрицей ступенчатого если:
1) все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками;
2) ведущий элемент (первый ненулевой элемент строки при отсчёте слева направо) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.
Вот пример матрицы ступенчатого вида:
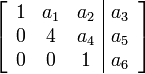
Матрица называется матрицей главного ступенчатого вида по строкам если она удовлетворяет дополнительному условию:
каждый ведущий элемент ненулевой строки – это единица.
Вот пример матрицы главного ступенчатого вида:

Метод Гаусса
Любую матрицу с помощью нескольких элементарных преобразований над строками можно привести к главному ступенчатому виду.
Определение 1. Элементарным преобразованием первого типа над строками какой-либо матрицы называется перестановка местами двух произвольных строк этой матрицы.
Определение 2. Элементарным преобразованием второго типа называется умножение произвольной строки данной матрицы на какое-либо число, не равное 0.
Определение 3. Элементарным преобразованием третьего типа называется прибавление к какой-либо строке данной матрицы другой строки, умноженной предварительно на любое число.
Решение. Выпишем расширенную матрицу данной системы
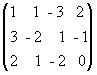
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
~ ;
;
б) третью строку умножим на (-5) и прибавим к ней вторую:
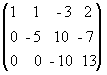 .
.
____________________________________________________________________________
№3
Система уравнений вида


называется системой линейных алгебраических уравнений с неизвестными x1, x2, …, xn.
Числа aij называются коэффициентами системы, bi − её свободными членами
Матрицей системы уравнений (1) называется матрица, составленная из коэффициентов системы:

Расширенной матрицей системы уравнений (1) называется матрица, составленная из коэффициентов системы и свободных членов:

Две системы уравнений относительно одного и того же набора неизвестных x1, x2, …, xn называются эквивалентными, или равносильными, если множества их решений совпадают, или, что то же, каждая из них является следствием другой.
Иными словами, две системы эквивалентны тогда и только тогда, когда каждое решение первой системы является решением второй и, наоборот, каждое решение второй системы является решением первой.
Предложение. При совершении одного элементарного преобразования система уравнений переходит в эквивалентную систему.
Доказательство. Достаточно доказать, что вторая система является следствием первой. Действительно, предположив, что это уже доказано, совершим обратное элементарное преобразование, которое вернёт нас к исходной системе. По доказанному первая система тогда будет следствием второй, и всё доказано.
Докажем, что вторая система является следствием первой. Для преобразований первых двух типов это совершенно очевидно. Совершим преобразование третьего типа, прибавив к i-й строке j-ю строку, умноженную предварительно на число α. При этом изменится только i-е уравнение, поэтому я здесь выпишу только его:
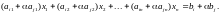
Пусть
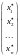 − какое-либо решение исходной (первой)
системы. Тогда по определению понятия
решения выполняются числовые равенства:
− какое-либо решение исходной (первой)
системы. Тогда по определению понятия
решения выполняются числовые равенства:

Если подставить наше решение в новую систему, то все равенства, кроме i-го, будут выглядеть точно так же и поэтому выполняются. i-е же равенство будет выглядеть так:

Чтобы убедиться, что оно тоже выполняется, достаточно взять i-е равенство системы (1*) верных числовых равенств и прибавить к нему j-е равенство той же системы, предварительно умножив его на α. Предложение доказано.
№4
Критерий совместности линейных уравнений
Система
совместна тогда и только тогда, когда
rank A =
rank D.
(Рангом
системы рядов ![]() называется
число рядов в ее максимальной линейно
независимой подсистеме
называется
число рядов в ее максимальной линейно
независимой подсистеме
![]() )
)
Правило Крамера
Если m
= n и ![]() то
система совместна и имеет единственное
решение
то
система совместна и имеет единственное
решение ![]() или,
что то же самое,
или,
что то же самое, ![]() где
где ![]() -
определитель, полученный из
det A заменой i-го
столбца столбцом свободных членов.
-
определитель, полученный из
det A заменой i-го
столбца столбцом свободных членов.
____________________________________________________________________________
№5
Метод Гаусса решения систем линейных уравнений |
Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме.Для того чтобы решить систему уравнений Рассмотрим метод Гаусса на примерах. Пример . Установить совместность и решить систему Решение. Выпишем
расширенную матрицу системы и поменяем
местами первую и вторую строки для
того, чтобы элемент
Имеем Выпишем
систему уравнений, расширенную матрицу
которой мы получили в результате
преобразований: Итак,
имеем |
____________________________________________________________________________
№6
Система однородных уравнений
Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю:
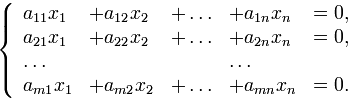
или, в матричном виде:
![]()
!
Однородная
система всегда совместна: она
имеет тривиальное решение: ![]() .
.
Задача
ставится о поиске нетривиального
решения. Оно не всегда существует. Так,
к примеру, если матрица ![]() системы
— квадратная и имеет ненулевой
определитель, то, согласно теореме
Крамера,
нетривиальных решений у однородной
системы нет. Теорема
Кронекера-Капеллиутверждает,
что условие
системы
— квадратная и имеет ненулевой
определитель, то, согласно теореме
Крамера,
нетривиальных решений у однородной
системы нет. Теорема
Кронекера-Капеллиутверждает,
что условие ![]() является
и достаточным для существования
нетривиального решения.
является
и достаточным для существования
нетривиального решения.
Т
Теорема. Для того, чтобы система однородных уравнений с квадратной матрицей имела нетривиальное решение необходимо и достаточно, чтобы (чтобы определитель был равен нулю).
____________________________________________________________________________
№7
Для того чтобы однородная система имела ненулевое решение, необходимо, чтобы число уравнений системы было меньше числа неизвестных.
Так как ранг матрицы из коэффициентов не может быть больше числа ее строчек (как и числа столбцов), то r<n, то, согласно теореме 1, система имеет ненулевое решение.
(Теорема 1. Если ранг матрицы А равен числу неизвестных, то система (1) имеет единственное (тривиальное) решение.
Действительно, согласно теоремы Крамера, r=n и решение единственное.
) ____________________________________________________________________________
№8
Если определитель данной матрицы =0, то строки (и столбцы) зависимы. А нет - так нет.
Пример
В ![]() векторы
векторы ![]() ,
, ![]() и
и ![]() линейно
независимы, так как уравнение
линейно
независимы, так как уравнение
![]()
имеет
только одно, тривиальное, решение.
Векторы
и ![]() являются
линейно зависимыми, так как
являются
линейно зависимыми, так как
![]()
а значит
![]()
Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A - λE) = 0
То-есть когда строки и столбцы зависимы
____________________________________________________________________________
№9
Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.
Любые два базиса линейного пространства состоят из одного и того же числа векторов.
Если
в линейном пространстве
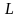 существует базис из
существует базис из
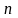 векторов, то пространство называют
конечномерным,
а
называют размерностью
линейного пространства
(пишут:
векторов, то пространство называют
конечномерным,
а
называют размерностью
линейного пространства
(пишут:
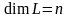 ).
).
Если
в линейном пространстве
для любого натурального
можно найти линейно независимую систему
векторов, то пространство называют
бесконечномерным
(пишут:
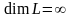 ).
).
ПРИМЕРЫ.
1)
Линейное пространство
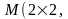 ℝ
ℝ матриц второго порядка с элементами
из ℝ имеет размерность
матриц второго порядка с элементами
из ℝ имеет размерность
 ℝ
ℝ .
Его базисом будут, например, матрицы
.
Его базисом будут, например, матрицы
 ,
,
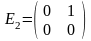 ,
,
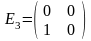 ,
,
 .
.
Базис
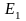 ,
,
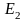 ,
,
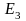 ,
,
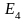 в дальнейшем будем называть стандартным
базисом
пространства
ℝ
.
в дальнейшем будем называть стандартным
базисом
пространства
ℝ
.
____________________________________________________________________________
№10
Элементарные преобразования СЛУ – преобразования одного из 3-х видов
1)Перестановка местами 2-х линейных уравнений
2)Умножение левой и правой части на ненулевое число
3)Прибавление к линейному уравнению любого другого уравнения, умножение на произвольное действительное число
Утверждение
В результате применения к СЛУ любого элемента преобразованная система преобразуется в равносильную
Равносильными или эквивалентными называются уравнения, множества корней которых совпадают
____________________________________________________________________________
№11
Базис - множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.
____________________________________________________________________________
№12
Что бы найти ранг матрицы надо:
Привести матрицу к ступенчатому виду(базистные столбцы)
Ранг матрицы равен количеству ступеней
Базис если:
ЛНЗ
Любой вектор из набора 1 можно записать набором 2
Число векторов в любом базисе одинакого
____________________________________________________________________________
№13
Определитель – это некоторое число поставленное в соответствие квадратной матрице.
определитель равен произведению всех чисел на главной диагонали.
____________________________________________________________________________
№14
а) Определитель (число) квадратной матрицы обозначается символами: detA=|A|
Свойства:
1)
При транспортировании матрицы значение
определителя не меняется, т.е. ![]() .
.
2) Если в определителе две строки (два столбца) пропорциональны, то он равен нулю. В частности, определитель равен нулю, если две строки (два столбца) совпадают или одна строка (столбец) нулевая.
3) Если поменять местами две строки (столбца), то определитель изменит свой знак на обратный.
4) Если строку (столбец) умножить на одно и то же число, то определитель умножится на это число.
5) Если к строке (столбцу) прибавить другую строку (столбец), умноженную на число, то определитель не изменится.
6)Нужно привести матрицу к треугольному виду (Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.) определитель равен произведению всех чисел на главной диагонали.
____________________________________________________________________________
№15
Невырожденная матрица ― квадратная матрица, определитель которой отличен от нуля. В противном случае она называетсявырожденной.
Для
квадратной матрицы ![]() над полем невырожденность
эквивалентна каждому из следующих
условий:
над полем невырожденность
эквивалентна каждому из следующих
условий:
обратима, то есть существует обратная матрица;
1 строки (столбцы) матрицы линейно независимы;
2 элементарными преобразованиями строк (столбцов) матрицу можно привести к единичной 3 матрице;
4 ранг матрицы равен её размерности.
____________________________________________________________________________
№16
Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
![]()
Способы нахождения обратной матрицы
Метод Гаусса
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При
использовании метода Гаусса первая
матрица будет умножаться слева на одну
из элементарных матриц ![]() (трансвекцию или диагональную
матрицу с
единицами на главной диагонали, кроме
одной позиции):
(трансвекцию или диагональную
матрицу с
единицами на главной диагонали, кроме
одной позиции):
![]() .
.
 .
.
Вторая
матрица после применения всех операций
станет равна ![]() ,
то есть будет искомой. Сложность
алгоритма —
,
то есть будет искомой. Сложность
алгоритма — ![]() .
.
С помощью матрицы алгебраических дополнений
![]()
![]() —
транспонированная матрица
алгебраических дополнений;
—
транспонированная матрица
алгебраических дополнений;
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
____________________________________________________________________________
№17
Определение. Подмножество L линейного координатного пространства Rn называется (линейным) подпространством, если выполняются следующие три условия:
1) x, y L x + y L;
2) x L, λ R (C) λx L;
3) 0 L.
Обозначение линейного подпространства: L ≤ Rn.
Примеры. 1. Очевидно, что подмножество, состоящее только из нулевого вектора (L = {0}), а также всё пространство (L = Rn) являются примерами подпространств. Это самое маленькое и самое большое подпространства.
2. А вот пример промежуточного подпространства, отличающегося от двух приведённых: в пространстве R3 рассмотрим множество векторов вида
L
= { ,
α, β
R}.
,
α, β
R}.
Таким образом, наше подмножество L состоит из трёхмерных векторов определённой структуры: первые две компоненты α и β − произвольные (действительные) числа, а третья компонента −α противоположна первой. Посмотрим, какой вид будет иметь сумма двух векторов такого вида:
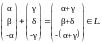
Снова получился вектор такой же структуры, т. е. принадлежащий L. Аналогично для умножения на скаляр:
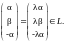
Кроме того, ясно, что 0 L, так что выполняются все три пункта определения, L − подпространство.
____________________________________________________________________________
№18
. Базис и размерность линейного подпространства
Определение. Пусть дано какое-то линейное подпространство L линейного пространства Rn (L ≤ Rn). Тогда система векторов a1, a2, …, ar Rn (1) называется базисом линейного подпространства, если выполняются следующие три условия:
1) a1, a2, …, ar L;
2) система (1) линейно независима;
3) каждый вектор подпространства L линейно выражается через векторы системы (1).
Базисов у подпространства (кроме нулевого) бесконечно много. Укажем один из базисов всего пространства Rn:
 (2)
(2)
Будем называть этот базис стандартным. Для доказательства того, что это действительно базис пространства Rn, вычислим линейную комбинацию:
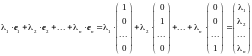 .
.
Исходя из этого равенства, легко доказываются все пункты определения базиса.
Теорема. Любая система из n + 1 вектора в пространстве Rn линейно зависима.
Доказательство. Пусть дана система из n + 1 вектора:
a1, a2, …, an, an+1 Rn. (1)
Рассмотрим стандартный базис:
e1, e2, …, en. (2)
Применив теперь к системам (1) и (2) лемму о двух системах векторов, получим, что система (1) линейно зависима.
Лемма. Пусть L − линейное подпространство пространства Rn. Если линейно независимая система векторов a1, a2, …, ak этого подпространства не является его базисом, то можно к ней добавить ещё один вектор ak+1 из L с сохранением линейной независимости.
Доказательство. Если каждый вектор из L линейно выражается через векторы исходной системы, то она является базисом L. В противном случае найдется вектор из L, который не выражается линейно через данную систему. Обозначим его через ak+1. Мы утверждаем, что система векторов
a1, a2, …, ak, ak+1
линейно независима. В самом деле, пусть
λ1a1 + λ2a2 + … + λkak + λk+1ak+1 = 0
и пусть λk+1 ≠ 0; тогда
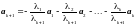 ,
,
т. е. вектор ak+1 линейно выражается через векторы системы a1, a2, …, ak, что противоречит выбору этого вектора. Значит, λk+1 = 0,
λ1a1 + λ2a2 + … + λkak = 0,
а тогда и все предыдущие коэффициенты λ1, λ2, …, λk равны нулю в силу линейной независимости системы a1, a2, …, ak.
Теорема. Любое линейное подпространство L пространства Rn, которое содержит хотя бы один ненулевой вектор, обладает базисом.
Доказательство. Возьмём в подпространстве L любой ненулевой вектор a1. Он образует линейно независимую систему из одного вектора. Если это базис L, то всё доказано. Если нет, то по лемме можно добавить вектор a2 L так, что система a1, a2 линейно независима. Если эта система является базисом подпространства L, то всё доказано. Если нет, то продолжаем процесс добавления векторов. На каком-то этапе, однако, мы всё же получим базис подпространства L. Иначе мы найдём в L линейно независимую систему из n + 1 вектора, что невозможно в силу предыдущей теоремы.
Примечание. Подпространство {0} не имеет базиса.
Теорема. Любые два базиса одного и того же подпространства содержат одно и то же количество векторов.
Доказательство проводится так же, как и для конечной системы векторов.
Определение. Если подпространство L не состоит из одного нулевого вектора, то количество векторов в любом его базисе называется размерностью подпространства L и обозначается dim L. Размерность подпространства {0} считается равной нулю.
____________________________________________________________________________
№19
Связь между общим и решением однородной и неоднородной систем.
Пусть ў – общее решение однородного уравнения(*), ?- некоторое решение неоднородного уравнения y(n) + a1(x) y(n-1) +…+an(x) y = b(x) (**). Тогда у= ў+ ? - общее решение неоднородного ур-я (**). Зная общее решение неоднородного ур-я, легко найти любое его частное решение.
____________________________________________________________________________
№20

 выписывают
расширенную матрицу этой системы
выписывают
расширенную матрицу этой системы  и
над строками этой матрицы производят
элементарные преобразования, приводя
ее к виду, когда ниже главной диагонали,
содержащей элементы
и
над строками этой матрицы производят
элементарные преобразования, приводя
ее к виду, когда ниже главной диагонали,
содержащей элементы 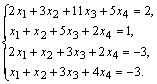
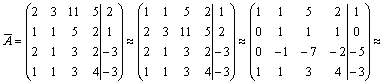
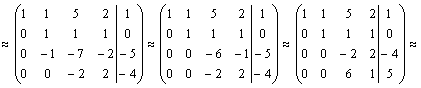
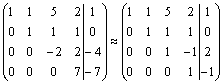 .
.