Свойства линейно зависимых и линейно независимых систем векторов

 1. Любая система векторов e₁,e₂, ..., e_k линейного пространства, содержащая нулевой вектор, линейно зависима.

2. Любая система векторов e₁,e₂, ..., e_k линейного пространства, содержащая пару взаимно противоположных векторов, линейно зависима.

3. Любая подсистема векторов линейно независимой системы векторов линейного пространства линейно независима.

4. Любая система векторов линейного пространства, содержащая линейно зависимую подсистему векторов, линейно зависима.

5. Система векторов линейного пространства линейно зависима тогда и только тогда, когда хотя бы один из векторов системы линейно выражается через остальные векторы системы (представлен в виде разложения по векторам системы).

6. Система векторов линейного пространства линейно независима любая её подсистемы векторов.

6. Система векторов, состоящая из одного ненулевого вектора линейного пространства, линейно независима.

Примеры:

Система векторов ·i, j линейного пространства R₂ геометрических радиусов векторов плоскости линейно независима.Действительно.

i = (1, 0),  j = (0, 1),   С₁·i + С₂· j = (С₁, С₂), а из (С₁, С₂) = 0 следует, что  С₁ = 0 и С₁ = 0, т.е. система векторов i, j из R₂ линейно независима.

///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

Система векторов ·i, j + k , i − j − k линейного пространства R₃ геометрических радиусов векторов трехиерного пространства линейно зависима.Действительно.

i = (1, 0, 0),  j = (0, 1, 0),   k = (0, 0, 1),    j +   k = (0, 1, 1), i − j − k = (1, −1, −1),

С₁·i + С₂· (j + k ) +С₂·( i − j − k) = (С₁+ С₃, С₂−С₃, С₂− С₃) = (0, 0, 0).

Последнее равенство выполнено, например, при С₁= −1, С₂= 1, С₃= 1.

Система векторов ·i, j + k , i − j − k линейно зависима.

Можно рассуждать иначе:

С₁·i + С₂· (j + k ) +С₂·( i − j − k) = (−1)·i + 1· (j + k ) + 1·( i − j − k) = −i + j + k + i − j − k = 0.

____________________________________________________________________________

№21

Любой вектор в пространстве может быть единственным образом разложен по базису е1, е2, е3 , т.е. вектор а=х1е1+х2е2+х3е3. вектор а представляет собой линейную комбинацию векторов е1, е2, е3..

Доказательство. 1) Пусть L произвольная прямая (или ось) и – базис . Возьмем произвольный вектор . Так как оба вектора  и  коллинеарные одной и той же прямой L, то . Воспользуемся теоремой о коллинеарности двух векторов. Так как , то найдется (существует) такое число , что  и тем самым мы получили разложение вектора  по базису  векторного пространства .

   Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису  векторного пространства :

 и , где . Тогда  и используя закон дистрибутивности, получаем:

                       .

Так как , то из последнего равенства следует, что , ч.т.д.

2) Пусть теперь Р произвольная плоскость и  – базис . Пусть  произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую , на которой лежит вектор , прямую , на которой лежит вектор . Через конец вектора  проведем прямую параллельную вектору  и  прямую параллельную вектору . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма , и , ,  – базис ,  – базис .

   Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа , что

   и . Отсюда получаем:

 и возможность разложения по базису доказана.

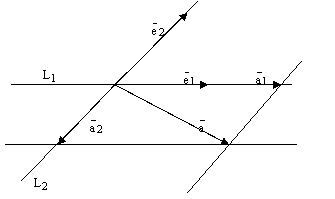
                                         рис.3.

   Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора  по базису  векторного пространства :  и . Получаем равенство

, откуда следует . Если , то , а т.к. , то  и коэффициенты разложения равны: , . Пусть теперь . Тогда , где . По теореме о коллинеарности двух векторов отсюда следует, что . Получили противоречие условию теоремы. Следовательно,  и , ч.т.д.