3) Пусть – базис и пусть произвольный вектор. Проведем следующие построения.

Отложим все три базисных вектора  и вектор  от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы , плоскость  и плоскость ; далее через конец вектора  проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:

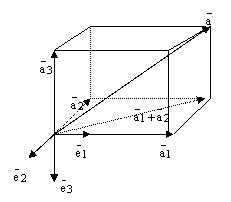
                             рис.4.

По правилу сложения векторов получаем равенство:

                        .                                    (1)

По построению . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число , такое что . Аналогично,  и , где . Теперь, подставляя эти равенства в (1), получаем:

                                             (2)

 и возможность разложения по базису доказана.

   Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису :

 и . Тогда

       .       (3)

   Заметим, что по условию векторы   некомпланарные, следовательно, они попарно неколлинеарные.

Возможны два случая:  или .

а) Пусть , тогда из равенства (3) следует:

           .                        (4)

Из равенства (4) следует, что вектор  раскладывается по базису , т.е. вектор  лежит в плоскости векторов  и, следовательно, векторы  компланарные, что противоречит условию.

б) Остается случай , т.е. .  Тогда из равенства (3) получаем  или

             .                           (5)

Так как – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что  и , ч.т.д.

Теорема доказана.

///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

Если система векторов e₁, ..., e_n n-мерного линейного пространства L_n образует базис в L_n, то любой вектор x из L_n может быть представлен в виде

x = С₁·e₁+ С₂·e₂+ ...+ С_n· e_n.

Выражение x = С₁·e₁+ С₂·e₂+ ...+ С_n· e_n называется разложением вектора по базису e₁, ..., e_n, а числа С₁, С₂, ..., С_n называются координатами вектора x  в базисе e₁, ..., e_n.

Координаты вектора принято обозначать тем же символом, что и сам вектор:

x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n.

Взаимно однозначное соответствие x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n ⇐⇒ x = (x₁, x₂, ..., x_n)

— изоморфизм L_n и R_n.

____________________________________________________________________________

№22

 —  -мерное векторное пространство над полем   с некоторыми базисами   и  .

Векторы одного базиса можно выразить через векторы другого:

.

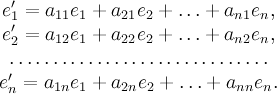Определение 4. Матрица, определенная коэффициентами вышеприведенного разложения

,

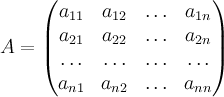называется матрицей перехода⁷⁾ от базиса   к базису  .

Теорема.   Матрица перехода   от базиса   к   невырождена.

 Для любого базиса   и любой невырожденной квадратной матрицы   порядка  существует и при том единственный базис   с матрицей перехода   , т.е.   .

Теорема. Если   -- матрица перехода от базиса   к   , то для любого вектора  справедливо равенство   , где   и   -- столбцы координат вектора   в базисах  и   соответственно, т.е.   .

Теорема 1. Преобразование координат вектора при переходе от "старого" базиса e к "новому" базису f определяется формулой:

X\f = C − 1X\e.

(2)

Доказательство. Обозначим координатные столбцы произвольного вектора x  X_n в "старом" базисе e

Xe =	     	x1 x2 … xn	     

и в "новом" базисе f

Xf =	     	x'1 x'2 … x'n	     

Произвольный вектор x в базисе e имеет вид:

x = eXe

(3)

В базисе f тот же вектор имеет вид:

x = fX_f

и в силу формулы (1)

x = eCXf.

(4)

Сравнивая формулы (3) и (4), получаем

X_\e = C · X_f.

Умножая это равенство слева на C ⁻¹ , получаем формулу (2), которую требовалось доказать.

Рассмотрим прямоугольную систему координат в трехмерном пространстве OXYZ. Вектору  в данном пространстве соответствует тройка чисел (x,y,z), являющихся проекциями вектора на оси Ox, Oy, Oz. Эти числа называются координатами вектора  .

Числа получаются как разность соответствующих координат точек A(x₀,y₀,z₀) и B(x₁,y₁,z₁):

x= x₁-x₀ , y= y₁-y₀ , z= z₁-z₀ а модуль вектора  , равный его длине, вычисляется по теореме Пифагора:

 .

2.7. Преобразование координат вектора при переходе к новому базису

Пусть   и  — два базиса в n-мерном линейном пространстве L.

Матрицей перехода от базиса   к базису   называется матрица C, столбцами которой являются координаты векторов  в базисе  :

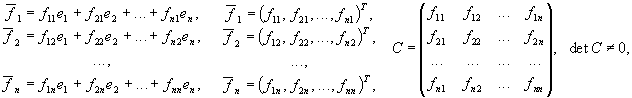
Вектор   линейно выражается через векторы обоих базисов. Тогда, если 

то координаты   вектора в базисе   , и его координаты   в базисе  связаны соотношениями

,

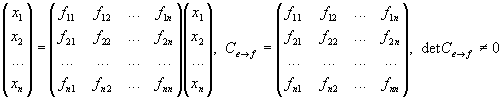или 

где  ,   — матрица перехода от базиса   к базису   и обратная к ней;   — векторы-столбцы координат вектора   в соответствующих базисах.

Таким образом доказана следующая

Теорема. Пусть (e)={ } и (f)={ }— два базиса в n-мерном линейном пространстве L.

Координаты  вектора  в базисе (e) и координаты   вектора  в базисе (f)связаны соотношением

где  ,   — матрица перехода от базиса (e) к базису (f) и обратная к ней.

____________________________________________________________________________

№23