Вопрос 11. Понятие числового ряда в комплексной области. Сходимость. Критерий Коши.

Пусть c_n=a_n+ib_n- последовательность комплексных чисел.

Определение. Выражение (1)

называется числовым рядом, числа c₁,…c_n,…- его членами.

-n-я частичная сумма ряда.

Определение. Если существует конечный предел последовательности частичных сумм, то ряд (1) называется сходящимся, а число S- его суммой. В этом случае пишут 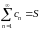. Если последовательность S_n расходится, то ряд называется расходящимся.

Теорема 1. Ряд (1) сходится тогда и только тогда, когда сходятся ряды (2) и (3). При этом, если A, B- суммы этих рядов, то имеет место равенство S=A+iB.

Доказательство следует из определения сходящегося ряда и соответствующей теоремы о пределах.

Теорема 2 (критерий Коши о сходимости ряда). Ряд (1) сходится тогда и только тогда, когда ε>0 N() :n>N() p выполнено S_n+p - S_n<ε.

Доказательство – как для рядов с действительными членами.

Как частный случай, получаем:

Теорема 3 (необходимое условие сходимости ряда). Если (1) сходится, то .

Определение. Ряд (1) называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов: . (4).

Ряд (4) – ряд с положительными действительными членами. Следовательно, о его сходимости можно судить на основании любого признака сходимости положительных рядов.

Теорема 4. Если ряд (1) сходится абсолютно, то он сходится.

Доказательство.

 Пусть c_n=a_n+ib_n. Так как , , то по общему признаку сравнения положительных рядов заключаем, что и сходятся, то есть ряды и сходятся абсолютно. Следовательно, они сходятся. Следовательно, по теореме 1 сходится ряд (1). 

Теорема 5. Ряд (1) сходится абсолютно тогда и только тогда, когда абсолютно сходятся ряды (2) и (3).

Доказательство.

 1) Необходимость. Пусть сходится. Так как a_nc_n и b_nc_n, то ряды и сходятся.

2) Достаточность. Пусть и сходятся. Так как c_n=a_n+ib_na_n+b_n, и сумма двух сходящихся рядов - сходящийся ряд, то сходится. 

Вопрос 12. Последовательности и ряды функций комплексного переменного

Сходимость. Критерий Коши. Признак Вейерштрасса.

Пусть (1) S_n(z) - последовательность функций комплексного переменного, определённая на некотором множестве E . Для произвольной точки z=z₀E получим числовую последовательность S_n(z₀). Если S_n(z₀) сходится (расходится), то S_n(z) сходится (расходится) в точке z=z₀. Множество всех точек z, в которых (1) сходится, называется областью сходимости последовательности (1).

Пусть (1) сходится на E. Тогда zE  . Ясно, что S(z) – функция от z,определенная на Е. Она называется предельной функцией последовательности (1). Сходимость последовательности (1) – поточечная.

Рассмотрим ряд (2),

членами которого являются функции комплексного переменного, определенные на Е.

Составим последовательность частичных сумм S_n(z)= , S_n(z)- функциональная последовательность. Если  на E, то ряд (2) сходится на E, и S(z) - его сумма. Эта сходимость поточечная.

Определение. Последовательность S_n(z) называется равномерно сходящейся на множестве E к предельной функции S_n(z), если ε>0 N() :n>N zE выполнено S_n(z) –S(z)<ε.

Определение1. Ряд называется равномерно сходящимся на Е к сумме S(z), если на этом множестве равномерно сходится последовательность его частичных сумм.

Теорема 1 (критерий Коши равномерной сходимости функционального ряда).

Ряд (2) равномерно сходится на множестве Е тогда и только тогда, когда ε>0 N() : n>N p zE выполнено S_n+p(z)-S_n(z)<ε .

Теорема 2 (признак Вейерштрасса). Пусть дан функциональный ряд (2).

Если n |f_n(z)|c_n zE, и сходится (c_n0, c_n ), то ряд (2) абсолютно и равномерно сходится на множестве E.

Доказательство.

 Т.к. 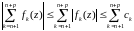, и ряд сходится, то согласно критерию Коши сходимости числового ряда 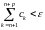n>N p . Отсюда

1) zE и, следовательно, ряд сходится, значит, сходится абсолютно на Е;

2) , значит, по теореме 1 ряд (2) сходится равномерно на Е. 

Аналогично случаю действительной переменной доказывается и следующие утверждения.

Теорема 3. Пусть . Если члены последовательности S_n(z) непрерывны на Е, и S_n(z)S(z) на Е, то S(z)- непрерывная функция.

Теорема 4. Если члены функционального ряда (2) непрерывны на Е и S(z) на Е, то его сумма S(z)- непрерывная функция.