Вопрос 1. Комплексные числа и действия над ними. Алгебраич. Форма записи числа. Геометрич. Интерпретация компл. Числа. Модуль и аргумент.

Определение. Комплексным числом z называется упорядоченная пара (a;y) действительных чисел x и y, то есть z= (x;y) , x,y .

Множество комплексных чисел обозначается , то есть ={z=(x;y) | x,y }.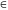

Комплексные числа z₁ =(x₁;y₁) и z₂=(x₂;y₂) называются равными, если x₁=x₂, y₁=y₂.

Пусть z=(x;y)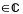 . Первая компонента пары называется вещественной (или действительной) частью, а вторая – мнимой частью комплексного числа z. Обозначается: x=Rez, y=Imz.

Определение. Суммой комплексных чисел z₁=(x₁;y₁) и z₂=(x₂;y₂) называется комплексное число z=z₁ +z₂ =(x₁ +x₂; y₁ +y₂).

Определение. Разностью двух комплексных чисел z₁=(x₁;y₁) и z₂=(x₂;y₂) называется комплексное число β, удовлетворяющее равенству z₂+z=z₁.

Очевидно, z=(x₁–x₂;y₁-y₂).

Определение. Произведением комплексных чисел z₁=(x₁;y₁) и z₂=(x₂;y₂) называется комплексное число z=z₁·z₂=(x₁·x₂-y₁·y₂; x₁·y₂+x₂·y₁).

Легко проверить, что операции сложения и умножения комплексных чисел подчиняются известным пяти законам арифметики:

1) z₁ +z₂=z₂ +z₁ (коммутативность сложения),

2) z₁ ·z₂=z₂ ·z₁ (коммутативность умножения),

3) z₁ +(z₂ +z₃)=(z₁+z₂)+z₃ (ассоциативность сложения),

4) z₁ ·(z₂·z₃)=(z₁·z₂)·z₃ (ассоциативность умножения),

5) z₁ ·(z₂+z₃)=z₁·z₂+z₁·z₃ (дистрибутивность умножения относительно сложения).

При y=0 комплексное число z =(x;0) отождествляется с действительным числом x. То есть множество действительных чисел является частью множества комплексных чисел. Из определения сложения и умножения следует, что

(x₁ ;0)+(x₂ ;0)=(x₁+x₂;0),(x₁ ;0)·(x₂ ;0)=(x₁·x₂;0),

т.е. операции над комплексными числами вида (x;0) совпадают с операциями над действительными числами.

При x=0 комплексное число z=(0;y) называется чисто мнимым. Комплексное число 0=(0;0) называется нулем. Комплексное число 1=(1;0) называется единицей, комплексное число i=(0;1) называется мнимой единицей.

Из определения сложения и умножения следует, что справедливы равенства:

z +0=z, z·0=0, z·1=z, i·i=i²=-1, i³ =i²·i=(-1)·i=-i,

i⁴ =i³·i=-i·i=-i² =-(-1)=1.

Следовательно, m,n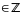 i^4·m+n=iⁿ.

Например, i⁵⁹ = i^4·14+3 =i³=-i.

На основе равенства i·y = (0;1)·(y;0)=(0;y) получается алгебраическая форма записи комплексного числа z=(x;y)=(x;0)+(0;y)=x+i·y,

z=x+i·y.

То есть всякое комплексное число z=(x;y) может быть представлено в виде суммы действительного числа x и чисто мнимого числа y·i.

Пусть z=x+i·y. Комплексное число =x–i·y называется сопряженным к числу z=x+i·y.

Из определения умножения получаем, что z·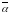 =x²+y² .

Геометрическая интерпретация комплексного числа. Модуль и аргумент комплексного числа.

В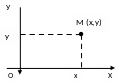 ыберем на плоскости систему координат. Комплексное число z=x+i·y=(x;y) можно понимать как точку М в декартовой координатной плоскости хОу с координатами (x;y). При таком отображении действительные числа изображаются точками оси абсцисс. Ось ОХ называется действительной осью. Чисто мнимые комплексные числа изображаются точками оси ординат. Ось ОУ – мнимая ось. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.

Можно установить взаимно-однозначное соответствие между точками пространства и множеством радиус-векторов точек координатной плоскости. То есть комплексное число z изображается вектором с началом в точке О и концом в точке М(х;у). При таком изображении комплексного числа z=x+i·y, числа x и у – проекции радиус-вектора z на оси координат.

Длина r вектора ОМ называется модулем комплексного числа z и обозначается |z|.

Итак, r=|z|= .

Угол φ - угол между положительным направлением оси ОХ и вектором ОМ называется аргументом комплексного числа z и обозначается: Arg z (-∞<φ< ∞).

Для числа z=0 аргумент не определён.

Для любого комплексного числа (кроме z=0) Arg z может быть найден из системы

которая имеет, вообще говоря, бесконечное множество решений. Все они содержатся в формуле φ=φ₀+2πk, k , где φ₀–одно из решений системы.

начение φ₀, удовлетворяющее условию -π <φ₀<π , называется главным значением аргумента и обозначается: arg z. Таким образом,

Arg z=argz+2πk, k .

Очевидно, что tg(arg z)=